
- •Задания к контрольной работе № 1
- •1) Методом Крамера систему а);
- •2) И методом Гаусса системы а) и б)
- •Задания к контрольной работе № 2
- •1. Вычислить интегралы:
- •2. Вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.
- •3. Найти объем тела, образованного вращением вокруг оси фигуры, расположенной в первом квадранте и ограниченной заданными параболой, прямой и осью. Сделать чертеж.
- •5. Решить задачи:
- •6. Всхожесть семян данного сорта растений оценивается вероятностью р. Посеяно n семян. Найти:
- •8. Завод сортовых семян выпускает гибридные семена кукурузы. Вероятность того, что семя 1-го сорта равна р . Найти:
- •1) Вероятность того, что диаметр наудачу взятой детали будет больше мм и меньшемм;
- •2) Вероятность того, что диаметр наудачу взятой детали отклонится от стандартной длины не более чем на мм.
- •Контрольная работа № 3.
- •1) Записать векторы в системе орт и найти модули этих векторов;
- •2) Найти угол между векторами и;
- •3) Найти проекцию вектора на вектор;
- •4) Написать уравнение плоскости, проходящей через точку с перпендикулярно вектору .
- •1) Длины сторон ав, вс, ас;
- •Контрольная работа № 4
- •Контрольная работа № 5
- •2) Дисперсию ;
- •3) Среднее квадратическое отклонение .
- •4) Построить многоугольник распределения;
- •5) Построить функцию распределения.
- •1) Вероятность попадания случайной величины в интервал;
1) Вероятность того, что диаметр наудачу взятой детали будет больше мм и меньшемм;
2) Вероятность того, что диаметр наудачу взятой детали отклонится от стандартной длины не более чем на мм.
1.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
2.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
3.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
4.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
6.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
7.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
8.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
9.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
11.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
12.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
13.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
14.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
15.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
16.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
17.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
18.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
19.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
20.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Контрольная работа № 3.
В задачах 1-20 решить системы уравнений методом Крамера:
1.
 2.
2.
3.
 4.
4.
5.
 6.
6.
7.
 8.
8.
9.
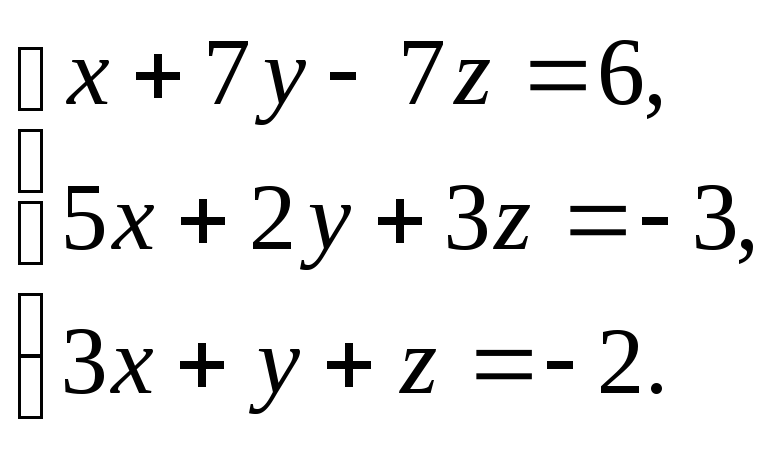 10.
10.
11.
 12.
12.
13.
 14.
14.
15.
 16.
16.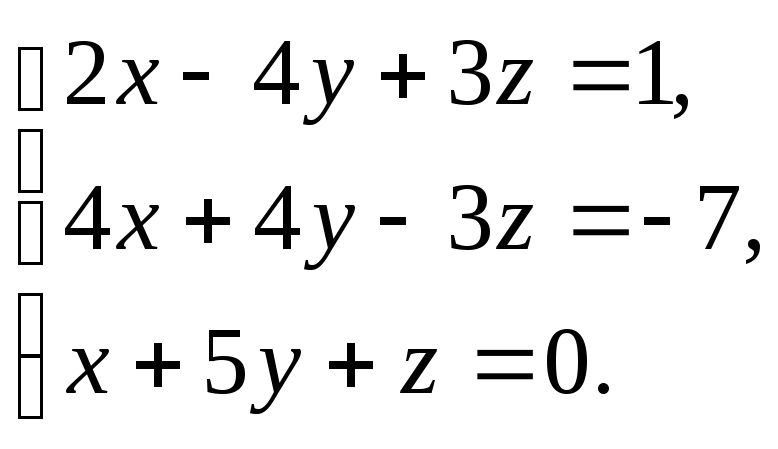
17.
 18.
18.
19.
 20.
20.
В задачах 21-40
даны векторы
![]() ,
,![]() ,
,![]() ,
,![]() .
Показать, что векторы
.
Показать, что векторы![]() ,
,![]() ,
,![]() образуют базис трехмерного пространства
и найти координаты вектора
образуют базис трехмерного пространства
и найти координаты вектора![]() в этом базисе.
в этом базисе.
21.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
22.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
23.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
24.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
25.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
26.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
27.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
28.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
29.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
30.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
31.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
32.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
33.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
34.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
35.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
36.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
37.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
38.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
39.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
40.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
В задачах 41-60 даны координаты вершин пирамиды АВСD. Требуется:
1) Записать векторы в системе орт и найти модули этих векторов;
2) Найти угол между векторами и;
3) Найти проекцию вектора на вектор;
4) Написать уравнение плоскости, проходящей через точку с перпендикулярно вектору .
41. А(2; -3; 1), В(6;1;-1), С(4; 8; -9), D(2; -1; 2).
42. А(5;-1;-4), В(9; 3;-6), С(7; 10; -14), D(5; 1; -3).
43. А(1;-4;0), В(5; 0;-2), С(3; 7; -10), D(1; -2; 1).
44. А(-3;-6;2), В(1; -2;0), С(-1; 5;-8), D(-3;-4; 3).
45. А(-1;1;-5), В(3; 5;-7), С(1; 12;-15), D(-1; 3; -4).
46. А(-4;2;-1), В(0; 6;-3), С(-2; 13;-11), D(-4; 4; 0).
47. А(0;4;3), В(4; 8;1), С(2; 15;-7), D(0; 6; 4).
48. А(-2;0;-2), В(2; 4;-4), С(0; 11;-12), D(-2; 2; -1).
49. А(3;3;-3), В(7; 7;-5), С(5; 14;-13), D(3; 5; -2).
50. А(4; -2;5), В(8; 2; 3), С(6; 9;-5), D(4; 0; 6).
51. А(-5; 0; 1), В(-4; -2; 3), С(6; 2; 11), D(3; 4; 9).
52. А(1; -4; 0), В(2; -6; 3), С(12; -2; 10), D(9; 0; 8).
53. А(-1; -2; -8), В(0; -4; -6), С(10; 0; 2), D(7; 2; 0).
54. А(0; 2; -10), В(1; 0; -8), С(11; 4; 0), D(8; 6; -2).
55. А(3; 1; -2), В(4; -1; 0), С(14; 3; 8), D(11; 5; 6).
56. А(-8; 3; -1), В(-7; 1; 1), С(3; 5; 9), D(0; 7; 7).
57. А(2; -1; -4), В(3; -3; -2), С(13; 1; 6), D(10; 3; 4).
58. А(-4; 5; -5), В(-3; 3; -3), С(7; 7; 5), D(4; 9; 3).
59. А(-2; -3; 2), В(-1; -5; 4), С(9; -1; 12), D(6; 1; 10).
60. А(-3; 4; -3), В(-2; 2; -1), С(8; 6; 7), D(5; 8; 5).
В задачах 61-80 даны вершины треугольника АВС. Найти:
1) Длины сторон ав, вс, ас;
2) уравнения сторон АВ, ВС, АС и их угловые коэффициенты;
3) внутренний угол А;
4) уравнение высоты СD и ее длину;
5) уравнение окружности, для которой высота СD является диаметром.
A(-5;0), B(7;9), C(5;-5).
A(-7;2), B(5;11), C(3;-3).
A(-5;-3), B(7;6), C(5;-8).
A(-6;-2), B(6;7), C(4;-7).
A(-8;-4), B(4;5), C(2;-9).
A(0;-1), B(12;8), C(10;-6).
A(-6;1), B(6;10), C(4;-4).
A(-2;-4), B(10;5), C(8;-9).
A(-3;0), B(9;9), C(7;-5).
A(-9;-2), B(3;7), C(1;-7).
A(-5;2), B(7;-7), C(5;7).
A(-7;5), B(5;-4), C(3;10).
A(-7;1), B(5;-8), C(3;6).
A(0;3), B(12;-6), C(10;8).
A(-8;4), B(4;-5), C(2;9).
A(-2;2), B(10;-7), C(8;7).
A(1;2), B(13;-7), C(11;7).
A(-4;1), B(8;-8), C(6;6).
A(-7;-1), B(-5;-10), C(3;4).
A(-4;8), B(5;-4), C(10;6).
В задачах 81-100 установить тип кривой и построить данную кривую.
81.
![]()
82.
![]()
83.
![]()
84.
![]()
85.
![]()
86.
![]()
87.
![]()
88.
![]()
89.
![]()
90.
![]()
91.
![]()
92.
![]()
93.
![]()
94.
![]()
95.
![]()
96.
![]()
97.
![]()
98.
![]()
99.
![]()
100.
![]()
В задачах 101-120 найти пределы:
101. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
102. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
103. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
104. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
105. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
106. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
107. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
108. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
109. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
110. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
111. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
112. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
113. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
114. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
115. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
116. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
117. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
118. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
119. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
120. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
В задачах 121 -140 найти производные указанных функций функций:
121. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
122. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
123. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
124. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
125. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
126. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
127. а)
![]() ;
б)
;
б)![]() в)
в)![]() .
.
128. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
129. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
130. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
131. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
132. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
133. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
134. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
135. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
136. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
137. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
138. а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
139. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
140. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
В задачах 141 -160 исследовать функции и построить графики.
141.
![]() 142.
142.
![]() 143.
143.
![]() 144.
144.
![]()
145.
![]() 146.
146.
![]() 147.
147.
![]() 148.
148.
![]()
149.
![]() 150.
150.
![]() 151.
151.
![]() 152.
152.
![]()
153.
![]() 154.
154.
![]() 155.
155.
![]() 156.
156.
![]()
157.
![]() 158.
158.
![]() 159.
159.
![]() 160.
160.
![]()
