Высшая математика / 4_24-33
.docГлава 2. Векторная алгебра
§ 1. Основные определения
Величины, характеризующиеся только числом, называются скалярными (длина, площадь, масса и т.д.).
Величины, которые характеризуются не только числом, но и направлением, называются векторными (сила, скорость, давление и т.д.).
В векторной алгебре имеют дело с геометрическим изображением векторной величины – вектором.
Определение 1. Вектором называется направленный отрезок определенной длины (направление задаётся указанием, какая из граничных точек есть начало, а какая – конец, и показывается стрелкой).
Обозначения:
если начало обозначить буквой A,
конец буквой B,
то вектор запишется
,
вектор может быть записан и строчной
буквой
,
и т.д. (см. рис.1).
Определение 2. Говорят, что два вектора равны, если один из них может быть получен параллельным переносом другого.
Определение
3. Модулем
вектора
называют длину отрезка, изображающего
вектор. Обозначения:
,
.
Определение 4. Векторы называются коллинеарными, если изображающие их отрезки лежат на одной или параллельных прямых.
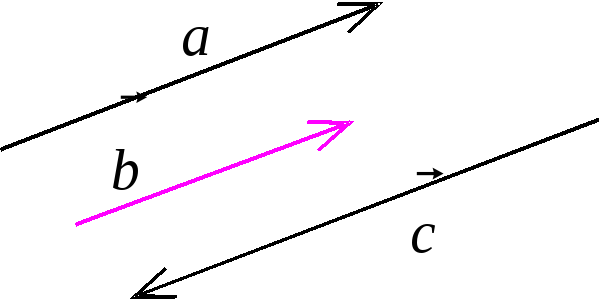
Рис .2
Определение 5. Векторы называются компланарными, если они лежат в одной или параллельных плоскостях.
На
рис. 3 плоскости Р,
Q
и R
параллельны, вектор
содержится в плоскости Р,
вектор
– в плоскости Q,
векторы
и
– в плоскости R.
Поэтому векторы
,
,
,
компланарны (рис. 3).
Определение
6. Нулевым
вектором
(обозначается
)
называют вектор, у которого начало
совпадает с концом.
Рис. 3
Определение
7. Два
коллинеарных вектора
и
называются
одинаково
(противоположно) направленными,
если у равных им векторов, имеющих общее
начало, концы расположены по одну сторону
(по разные стороны) от начала.
Обозначения:
↑↑
(
↑↓
).
На
рис. 2
↑↑
и
↑↓
.
Из
определений 2, 3 и 7 следует, что если
векторы
и
равны, то
и направления
и
совпадают.
§ 2. Линейные операции над векторами
Определение 1. Линейными операциями над векторами называются операции сложения, вычитания векторов и умножения вектора на число.
Определение
2. (Правило
треугольника)
Суммой
векторов
и
называется третий вектор
,
такой, что начало вектора
совпадает с началом вектора
,
а конец вектора
совпадает с концом вектора
(при условии,
что конец вектора
совпадает с началом вектора
)
(см. рис. 4).
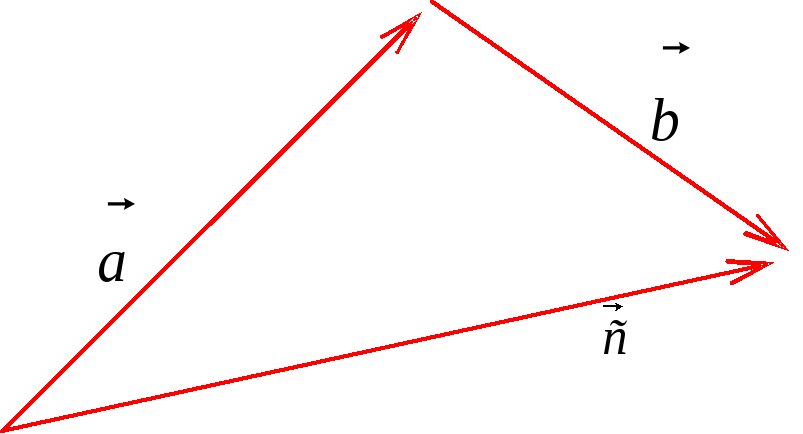
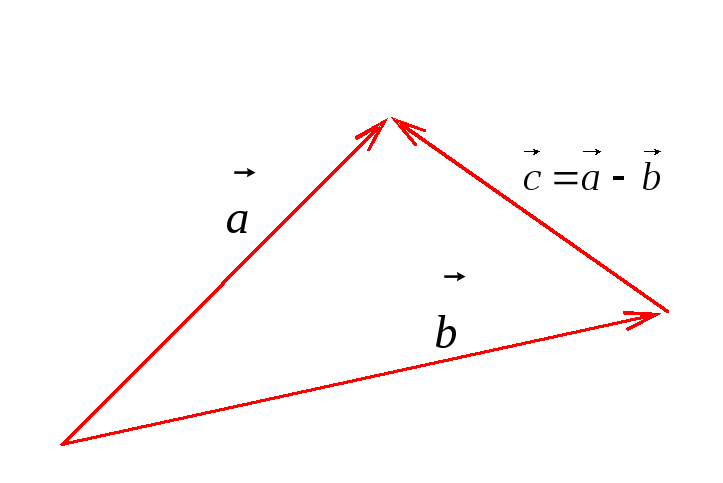
Рис. 4 Рис. 6
Свойство:
(см. рис. 8).
Для сложения любого конечного числа векторов справедливо правило треугольника, которое в таком случае называется правилом многоугольника.
Для
того чтобы сложить n
векторов
,
надо к концу первого вектора присоединить
начало второго, к концу второго – начало
третьего и т.д. до тех пор, пока к концу
n–1-го
вектора не присоединится начало n-го,
а затем начало первого вектора соединить
с концом n-го.
Начало вектора суммы
совпадает с началом
,
а конец – с концом
(см. рис. 5).
Определение
3. Разностью
векторов
и
называется третий вектор
,
который в сумме с вектором
даёт вектор
,
то есть
(см. рис. 6).
Определение
4.
Произведением
вектора
на число
называется вектор
такой, что:
1)
;
2)
направление вектора
совпадает с
направлением вектора
,
если
> 0; направление
вектора
противоположно
направлению вектора
,
если
< 0. Если
= 0 или
= 0,
то
.
Условие коллинеарности векторов
Пусть
векторы
и
коллинеарны.
Теорема
1
(необходимое
и достаточное условие коллинеарности
векторов).
Для того
чтобы два вектора
и
были коллинеарны, необходимо и достаточно,
чтобы существовало такое число ,
что
.
Из
определения понятия произведения
вектора на число следует, что
(см. рис. 7).
Рис. 7
Рис. 8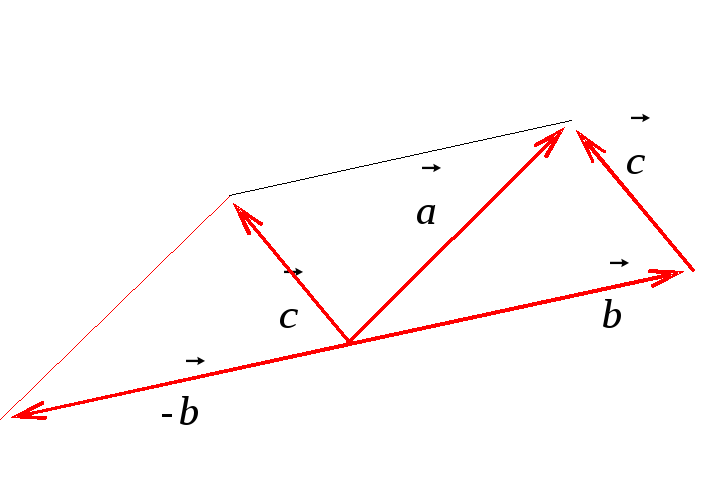
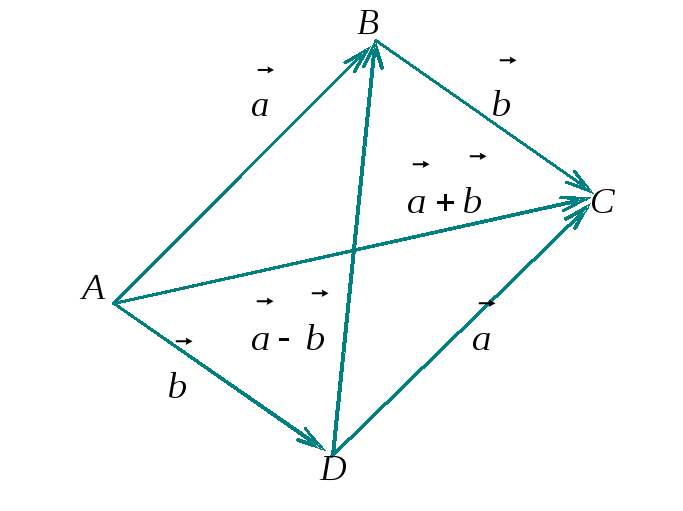
Рассмотрим
параллелограмм АВСD
(рис. 8). Из определения 2 следует, что
.
Так как в параллелограмме
,
то
.
Таким
образом, можно сформулировать следующее
правило сложения векторов (правило
параллелограмма):
суммой двух
векторов
и
,
приложенных к одному началу, является
вектор
,
совпадающий с диагональю параллелограмма,
построенного на этих векторах.
Из
определения 3 разности векторов следует,
что вектор
,
совпадающий со второй диагональю
параллелограмма, равен разности векторов
и
,то
есть
.
§ 3. Взаимное расположение вектора и оси; двух векторов
Определение 1. Прямая с выбранным на ней направлением называется осью.
Пусть
заданы вектор
и ось
l. Для простоты
изложения будем считать, что вектор
и ось
l лежат в
одной плоскости. Опустим перпендикуляры
из точек А
и В
на ось l
и рассмотрим вектор
,
где основания перпендикуляров точки
и
есть
проекции точек А
и В
на ось l (cм.
рис. 9.).
Рис. 9
Определение
2. Проекцией вектора
на ось
l (пр
)
называется
число, равное
,
если
,
и
,
если
.
Определение
3. Ортом
оси l называется вектор
,
модуль которого равен 1,
а направление совпадает с направлением
оси l.
Определение 4. Углом между двумя векторами (или между вектором и осью) называется наименьший угол , на который нужно повернуть один из векторов, чтобы его направление совпало с направлением другого вектора (или направлением оси) (0 180).
Угол
между двумя векторами или между вектором
и осью будем обозначать:
или
.
Свойство
1. пр
пр
+ пр
(см. рис. 10).
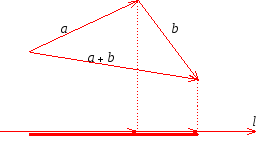
Рис. 10
Свойство
2. пр
=
(см. рис. 11).
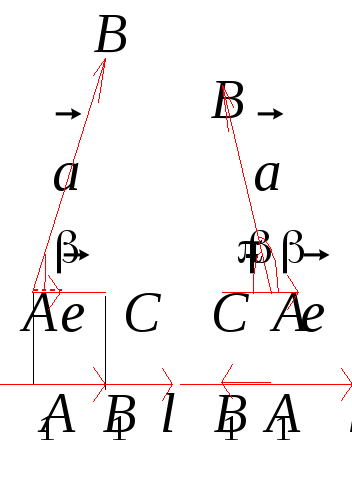
Рис. 11
пр
=
=АС=
=
=
пр
=
=
=
=
=
.
§ 4. Прямоугольная декартова система координат на плоскости.
Вектор в системе координат
Определение 1. Ось с выбранным на ней началом отсчёта и единицей длины называется координатной осью.
Определение 2. Упорядоченная система двух взаимно перпендикулярных координатных осей с общим началом О и общей единицей длины называется прямоугольной декартовой системой координат на плоскости.
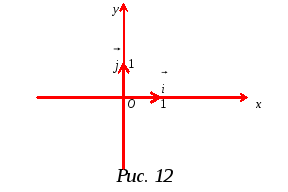
Обычно
рассматривают систему координат хОу,
состоящую из двух координатных осей Ох
и Оу,
где Ох
– горизонтальная ось, направленная
вправо (ось абсцисс), а Оу
– вертикальная ось, направленная вверх
(ось ординат). Будем обозначать орты
осей Ох
и Oy,
соответственно,
(cм.
рис. 12.). Говорят, что векторы
образуют декартов базис на плоскости.
Пусть
в системе координат хОу
задан некоторый вектор
.
Будем считать, что
имеет начало в точке О. Пусть конец
вектора
есть точка М.
Обозначим проекции вектора
на оси Ох,
Oy
через
соответственно (см. рис. 13). Тогда
.
Числа
называются координатами
вектора
в базисе
.
Будем
обозначать:
.
Если
начало вектора
лежит в точке
,
а конец в точке
,
то координаты вектора
находятся по формуле
,
,
то есть из координат конца вектора
вычитаются координаты начала вектора.
Теорема
1.
Модуль (длина) вектора находится по
формуле
,
если
и
,если
координаты начала и конца вектора
заданы, соответственно, точками
и
.
Пример
Найти
модуль вектора
.
Решение:
.
Пример
Найти
модуль вектора
,
если
и
.
Решение:
.
Теорема
2. Если
и
,
то
и
.
Пример
Найти
,
если
,
.
Решение:
.
Теорема3.
Если
,
то
.
Пример
Найти
,
если
.
Решение:
.
§ 5. Прямоугольная декартова система координат в пространстве. Вектор в системе координат
Определение 1. Упорядоченная система трёх взаимно перпендикулярных координатных осей с общим началом О и общей единицей длины называется прямоугольной декартовой системой координат в пространстве.
Ось
Ох
называют осью абсцисс, ось Оу
– осью ординат, ось Оz
– осью аппликат. Орты осей Ох,
Oy,
Oz
будем обозначать соответственно
.
Векторы
иногда называют базисной тройкой или
просто базисом.
Обычно
в пространстве рассматривают декартову
систему координат, расположенную таким
образом, что при наблюдении с конца
вектора
кратчайший поворот от
к
происходит против часовой стрелки (рис.
14).
Пусть
в системе координат задан некоторый
вектор
.
Так как равные векторы – это векторы,
один из которых может быть получен
параллельным переносом другого, то
будем считать, что
имеет начало в точке О. Пусть конец
вектора
есть точка М.
Обозначим проекции вектора
на оси Ох,
Oy,
Oz
через
соответственно (рис. 15). Тогда можно
доказать, что
.
Числа
называются координатами
вектора
в базисе
.
Будем
обозначать:
.
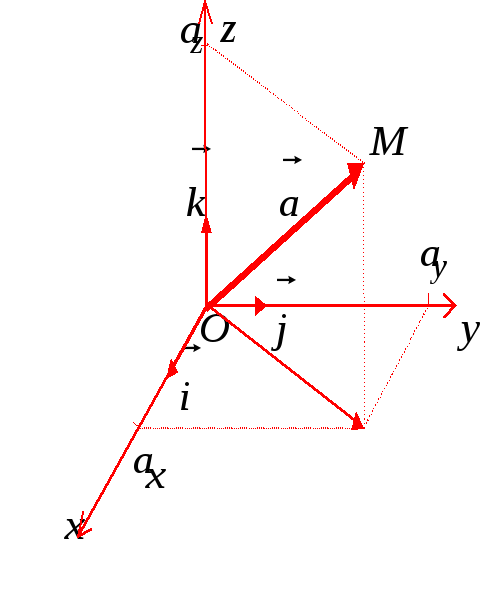
Рис. 14 Рис. 15
Если
начало вектора
лежит в точке
,
а конец в точке
,
то координаты вектора
находятся по формуле
,
,
,
то есть из координат конца вектора
вычитаются координаты начала вектора.
Теорема
1. Модуль
(длина) вектора находится по формуле
,
если
и
,
если координаты
начала и конца вектора заданы,
соответственно, точками
и
.
Пример
Найти
модуль вектора
.
Решение:
.
Пример
Найти
модуль вектора
,
если
и
.