
Задачи для самостоятельной работы Элементы линейной алгебры
1. Вычислить определители второго порядка:
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
2. Решить неравенство:
1)
![]() 2)
2)
![]()
3. Вычислить определители третьего порядка:
1)
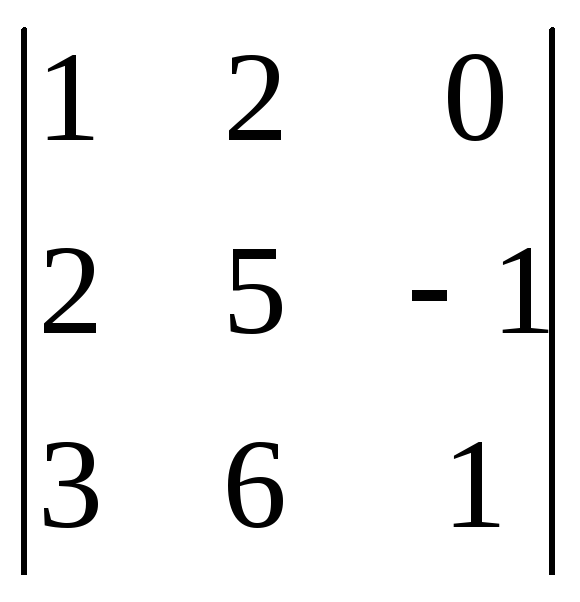 2)
2)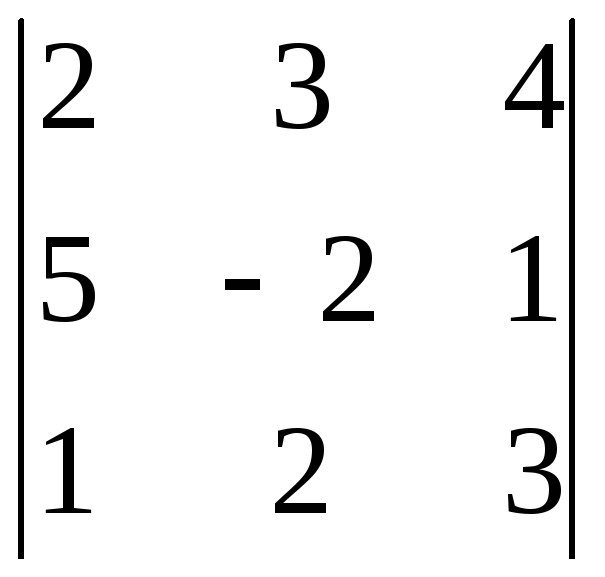 3)
3)
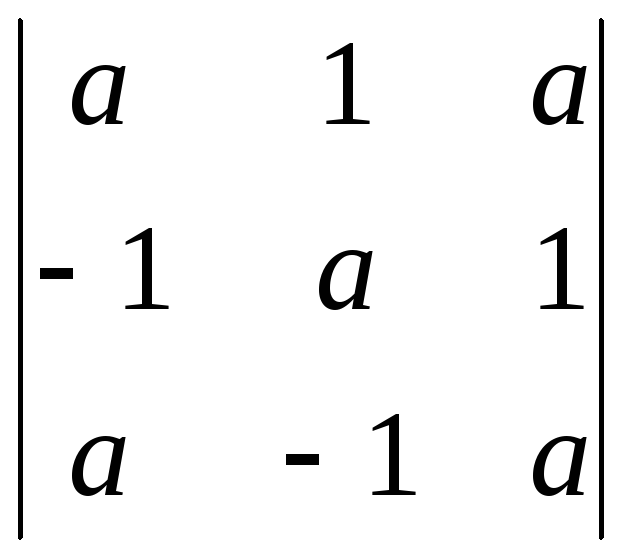 4)
4)
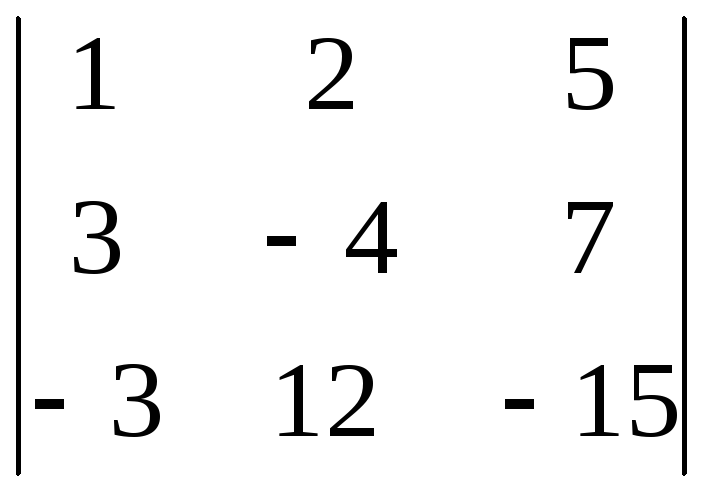
5)
 6)
6)
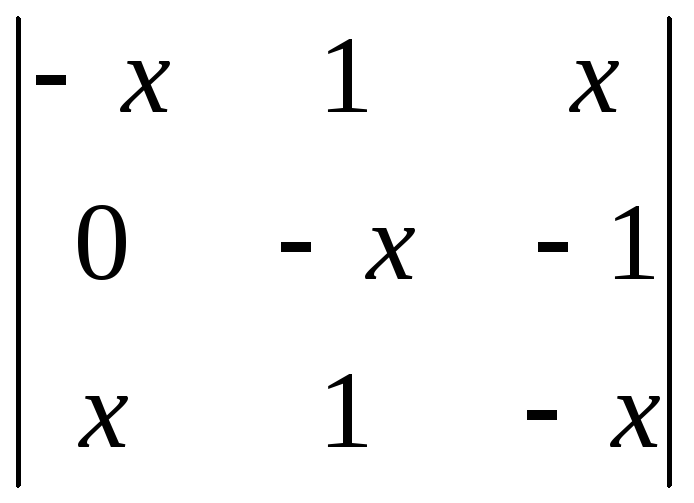 7)
7)
 8)
8)

4. Найти
![]() из уравнений
из уравнений
1)
 2)
2)

И проверить подстановкой корней в определитель.
5. Решить системы методом Крамера:
1)
 2)
2)

6. Решить системы методом Крамера:
1)
 2)
2)

3)
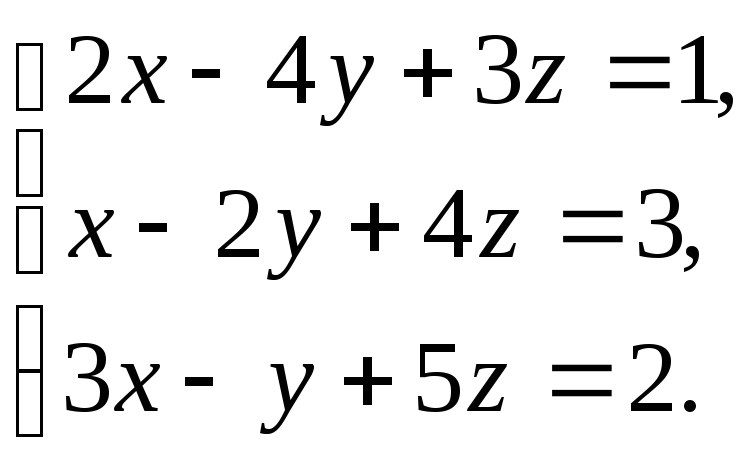 4)
4)
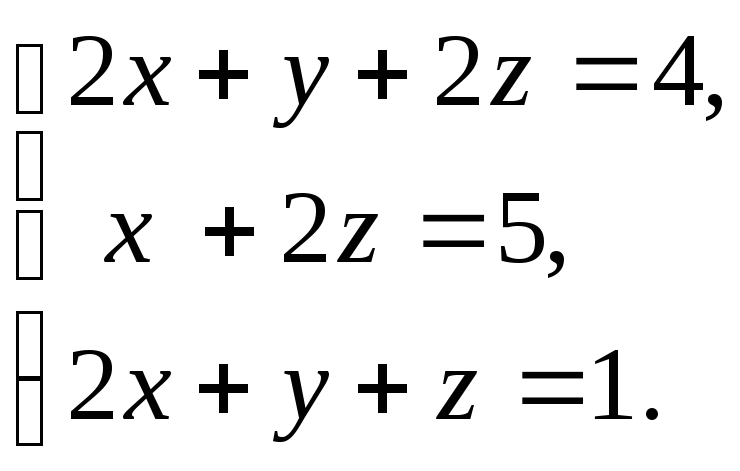
7. Решить системы методом Гаусса:
1)
 2)
2)
 3)
3)
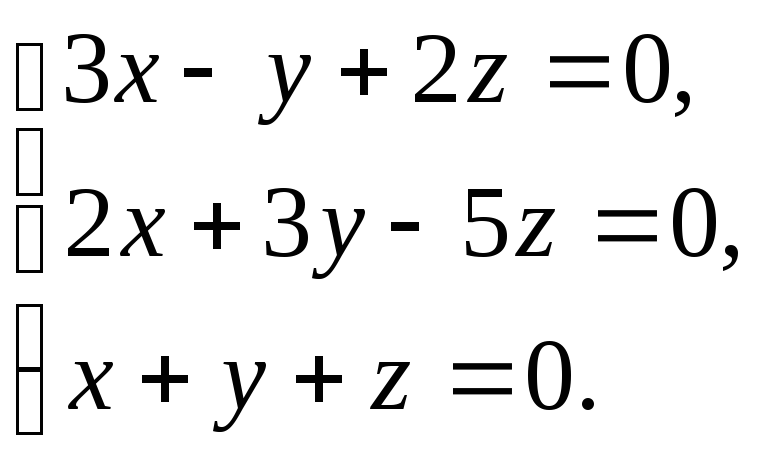
4)
 5)
5)
 6)
6)

7)
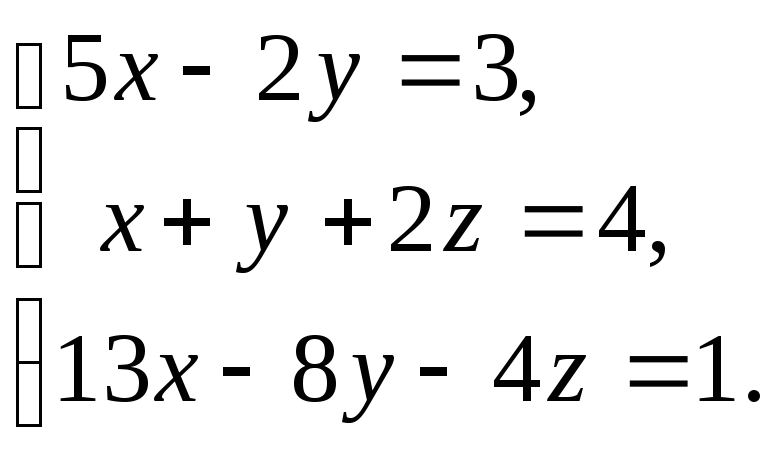 8)
8)
 9)
9)

10)
 11)
11)
 12)
12)

Векторная алгебра
8

 .
По сторонам ОА
и ОВ
прямоугольника ОАСВ
отложены единичные векторы
.
По сторонам ОА
и ОВ
прямоугольника ОАСВ
отложены единичные векторы
![]() и
и
![]() .
Выразить через
.
Выразить через
![]() и
и
![]() векторы
векторы
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() и
и
![]() ,
если
,
если
![]() и
и
![]() (рис.
1).
(рис.
1).
9. Пусть на рис. 1
точка М –
середина ВС
и точка N
– середина АС.
Определить векторы
![]() ,
,
![]() и
и
![]() при
при
![]() и
и
![]() (рис.
1).
(рис.
1).
10. Даны векторы
![]() ,
,
![]() .
Выразить векторы
.
Выразить векторы
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() через векторы
через векторы
![]() и
и
![]() (рис. 2).
(рис. 2).
11. Даны векторы
![]() ,
,
![]() ,
,
![]() .
Построить векторы
.
Построить векторы
![]() ,
,
![]() ,
,
![]() .
Каким диагоналям соответствуют
алгебраические суммы векторов (рис. 3).
.
Каким диагоналям соответствуют
алгебраические суммы векторов (рис. 3).
12. На трех
некомпланарных векторах
![]() ,
,
![]() и
и
![]() (рис. 3) построен параллелепипед. Указать
те его вектор–диагонали, которые
соответственно равны
(рис. 3) построен параллелепипед. Указать
те его вектор–диагонали, которые
соответственно равны
![]() ,
,
![]() ,
,
![]() .
.
13. Доказать аналитически и графически равенства:
1)
![]() 2)
2)
![]()
14. Даны векторы
![]() ,
,
![]() .
Вектор
.
Вектор
![]() – медиана
– медиана
![]() .
Разложить аналитически и геометрически:
1) вектор
.
Разложить аналитически и геометрически:
1) вектор
![]() по векторам
по векторам
![]() и
и
![]() ;
2) вектор
;
2) вектор
![]() по векторам
по векторам
![]() и
и
![]() .
.
15. На плоскости
даны точки
![]() ,
,
![]() и
и
![]() .
В начале координат приложены силы
.
В начале координат приложены силы
![]() ,
,
![]() и
и
![]() .
Построить равнодействующую
.
Построить равнодействующую
![]() ,
найти ее проекции на оси координат и
величину. Выразить силы
,
найти ее проекции на оси координат и
величину. Выразить силы
![]() ,
,
![]() ,
,
![]() и
и
![]() через единичные векторы
через единичные векторы
![]() и
и
![]() координатных осей.
координатных осей.
16.Даны точки
![]() и
и
![]() .
Построить вектор
.
Построить вектор
![]() и определить его длину и направление.
и определить его длину и направление.
17. Даны три вершины
параллелограмма АВСD
точки![]() ,
,
![]() и
и
![]() .
Доказать, что АВСD
есть квадрат (различными способами).
.
Доказать, что АВСD
есть квадрат (различными способами).
18. На плоскости
![]() даны точки
даны точки
![]() ,
,
![]() и
и
![]() и построены векторы
и построены векторы
![]() ,
,
![]() и
и
![]() .
Разложить геометрически и аналитически
вектор
.
Разложить геометрически и аналитически
вектор
![]() по векторам
по векторам
![]() и
и
![]() .
.
19. Найти координаты
точки
![]() через векторы
через векторы
![]() ,
,
![]() и
и
![]() параллелограмма
ABCD,
если
параллелограмма
ABCD,
если
![]() ,
,![]() ,
,
![]() .
Найти модули сторон и диагоналей
параллелограмма. Найти координаты и
модули векторов
.
Найти модули сторон и диагоналей
параллелограмма. Найти координаты и
модули векторов
![]() ,
,
![]() .
.
20. Вектор составляет
с осями
![]() и
и
![]() углы 60
и 120.
Какой угол он составляет с осью
углы 60
и 120.
Какой угол он составляет с осью
![]() ?
?
21. Даны три
последовательные вершины параллелограмма
![]() и
и
![]() и
и
![]() .
Найти его четвертую вершину
.
Найти его четвертую вершину
![]() .
.
22. На плоскости
![]() построить векторы
построить векторы
![]() ,
,
![]() и
и
![]() .
Разложить геометрически и аналитически
вектор
.
Разложить геометрически и аналитически
вектор
![]() по векторам
по векторам
![]() и
и
![]() .
.
23. Дано
![]() ,
,
![]() .
Найти скалярное произведение векторов
.
Найти скалярное произведение векторов
![]() и
и
![]() (двумя способами).
(двумя способами).
24. Определить угол
между векторами
![]() и
и
![]() .
.
25. Определить углы
![]() с вершинами
с вершинами
![]() ,
,
![]() и
и
![]() .
.
26. Из вершины квадрата проведены прямые, делящие противоположные стороны пополам. Найти угол между этими прямыми.
27. Найти угол между
диагоналями параллелограмма, построенного
на векторах
![]() и
и
![]() .
.
28. На плоскости
дан треугольник с вершинами
![]() ,
,
![]() и
и
![]() .
Найти угол, образованный стороной
.
Найти угол, образованный стороной
![]() и медианой
и медианой
![]() этого треугольника.
этого треугольника.
29. Даны векторы
![]() и
и
![]() .
Определить
.
Определить
![]() и
и
![]() .
.
30. Разложить векторы
![]() ,
,
![]() и
и
![]() в базисе 1)
в базисе 1)
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,![]() и
3)
и
3)
![]() ,
,![]() аналитически и графически, если
аналитически и графически, если
![]() ,
,
![]() ,
,
![]() .
.
31. Найти угол между
сторонами и диагоналями параллелограмма,
построенного на векторах
![]() и
и
![]() .
.
32. Найти координаты
векторов
![]() и
и
![]() ,
если
,
если
![]() ||
||
![]() .
.
