
- •§1.Схема построения графиков
- •§2.Преобразования графиков
- •§3. Графики основных элементарных функций
- •3.1. Степенная функция
- •3.2. Показательная функция
- •3.3 Логарифмическая функция
- •3.4 Тригонометрические функции
- •3.5 Обратные тригонометрические функции
- •§4. Построение кривых, заданных параметрически
- •§5. Построение кривых, заданных уравнением в полярных координатах.
§4. Построение кривых, заданных параметрически
Рассмотрим
способы построения кривых, заданных
системой уравнений вида
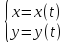 ,
,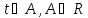 .
.
В
ряде случаев эту систему можно решить,
получив уравнение, связывающее переменные
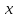 и
и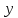 .
Например, система
.
Например, система
 ,
,
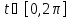 ,
дает уравнение
,
дает уравнение
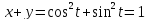 .
Учитывая, что множеством значений
.
Учитывая, что множеством значений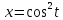 ,
,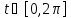 ,
является отрезок
,
является отрезок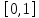 ,
получаем, что исходная система уравнений
задаёт функцию
,
получаем, что исходная система уравнений
задаёт функцию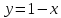 ,
определенную на отрезке
,
определенную на отрезке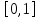 .
Из курса аналитической геометрии также
известно, что уравнения
.
Из курса аналитической геометрии также
известно, что уравнения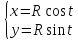 ,
,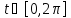 задают окружность радиуса
задают окружность радиуса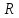 ,
а также уравнения
,
а также уравнения ,
, ,
задают эллипс с полуосями
,
задают эллипс с полуосями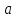 и
и .
.
Если
явно выразить
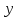 через
через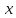 не удается, то используется схема,
которую мы дадим на примере построения
кривой, заданной системой уравнений
не удается, то используется схема,
которую мы дадим на примере построения
кривой, заданной системой уравнений ,
,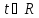 .
.
Начнем
с построения графика функции
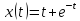 .
Эта функция непрерывна на всей числовой
прямой,
.
Эта функция непрерывна на всей числовой
прямой,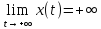 ,
,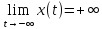 .
Первое из этих утверждений очевидное,
второе следует из того, что
.
Первое из этих утверждений очевидное,
второе следует из того, что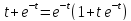 .
Далее, при
.
Далее, при функция
функция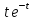 стремится к 0 (применяется правило
Лопиталя), а функция
стремится к 0 (применяется правило
Лопиталя), а функция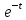 стремится к
стремится к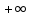 при
при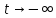 .
.
Производная
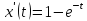 .
При
.
При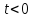 выполнено неравенство
выполнено неравенство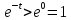 и
и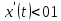 ,
поэтому
,
поэтому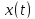 убывает. При
убывает. При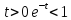 ,
поэтому
,
поэтому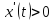 и функция возрастает. Наименьшего
значения функция
и функция возрастает. Наименьшего
значения функция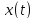 достигает при
достигает при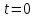 ,
,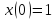 .
При этом и
.
При этом и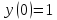 .
.
График
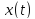 имеет вид:
имеет вид:
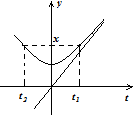
Каждому
значению
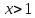 соответствуют два значения
соответствуют два значения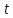 ,
обозначим их
,
обозначим их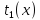 и
и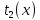 ,
причем
,
причем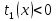 ,
,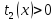 .
.
Так
как функция
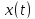 непрерывна и убывает при
непрерывна и убывает при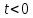 ,
функция
,
функция также непрерывна и возрастает при
также непрерывна и возрастает при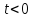 ,
а так как
,
а так как непрерывна и возрастает при
непрерывна и возрастает при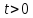 ,
,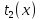 также непрерывна и возрастает (мы
использовали теорему об обратной
функции).
также непрерывна и возрастает (мы
использовали теорему об обратной
функции).
Следовательно,
по теореме о непрерывности сложной
функции
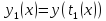 и
и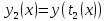 - также непрерывные.
- также непрерывные.
Исследуем
асимптотическое поведение функций
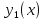 и
и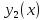 при
при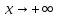 .
При
.
При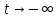 функция
функция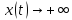 и
и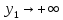 ,
так как
,
так как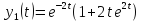 ,
,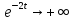 ,
а
,
а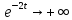 .
Так как
.
Так как
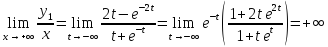 ,
,
функция
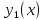 не имеет наклонной асимптоты.
не имеет наклонной асимптоты.
При
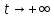 функция
функция и функция
и функция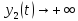 ,
при этом
,
при этом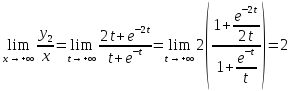 .
Наконец,
.
Наконец,
 .
.
Поэтому
прямая
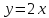 является наклонной асимптотой для
является наклонной асимптотой для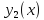 .
.
Вычислим
производные функций
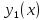 и
и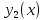 .
Обе они получаются по формуле
.
Обе они получаются по формуле .
При
.
При получаем, что
получаем, что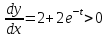 ,
поэтому, как
,
поэтому, как ,
так и
,
так и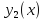 - возрастающие функции.
- возрастающие функции.
В
точке
 обе функции
обе функции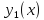 и
и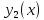 имеют первую производную, равную
имеют первую производную, равную .
.
Наконец,
вторая производная равна
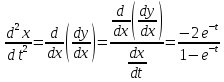 .
.
Поэтому
при
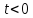 получаем
получаем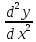 ,
кривая
,
кривая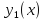 выгнута вверх, а при
выгнута вверх, а при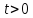
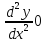 ,
кривая
,
кривая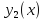 выгнута вниз.
выгнута вниз.
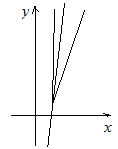
Комментарий
к графику:
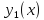 и
и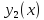 дают «клюв» - имеют особую правую
касательную с тангенсом угла наклона
в
дают «клюв» - имеют особую правую
касательную с тангенсом угла наклона
в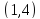 равным 4.
равным 4.
§5. Построение кривых, заданных уравнением в полярных координатах.
Рассмотрим
задачу построения на плоскости
 ,
введенной прямоугольной декартовой
системой координат, кривой, уравнение
которой имеет вид
,
введенной прямоугольной декартовой
системой координат, кривой, уравнение
которой имеет вид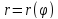 .
При этом мы считаем, что начало координат
совпадает с полюсом полярной системы
координат и что ось абсцисс совпадает
с полярной осью. В этом случае для
декартовых координат точки
.
При этом мы считаем, что начало координат
совпадает с полюсом полярной системы
координат и что ось абсцисс совпадает
с полярной осью. В этом случае для
декартовых координат точки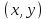 ,
имеющей полярные координаты
,
имеющей полярные координаты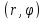 ,
выполняются равенства
,
выполняются равенства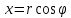 ,
,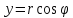 и уравнение
и уравнение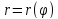 равносильно системе
равносильно системе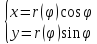 .
.
Поэтому
задание кривой полярным уравнением
 можно рассматривать, как частный случай
задания кривой системой параметрических
уравнений.
можно рассматривать, как частный случай
задания кривой системой параметрических
уравнений.
Рассмотрим несколько примеров.
Уравнение
 или
или ,
т.е. задает прямую линию на плоскости.
,
т.е. задает прямую линию на плоскости.
Построим
кардиоиду,
заданную уравнением
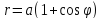 ,
,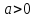 .
.
Так
как функция периодическая, с периодом
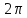 ,
рассматриваем
,
рассматриваем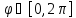 .
Так как функция чётная, достаточно
построить кривую
.
Так как функция чётная, достаточно
построить кривую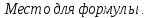 ,
а затем отразить ее симметрично полярной
оси, т.е. оси абсцисс. При
,
а затем отразить ее симметрично полярной
оси, т.е. оси абсцисс. При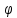 ,
меняющейся от
,
меняющейся от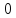 до
до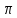 ,
величина
,
величина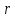 убывает от значения
убывает от значения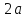 до
до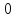 .
Поэтому эскиз части кривой при
.
Поэтому эскиз части кривой при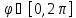 имеет примерный вид:
имеет примерный вид:
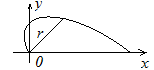
Эскиз всей кривой получаем отражением относительно полярной оси.
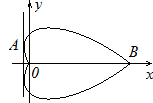
Осталось
ответить на два естественных вопроса.
Первый из них: чему равна абсцисса точки
 ?
Второй вопрос – о выпуклости кривой.
Для получения ответов на эти вопросы
рассмотрим параметрические уравнения
части кардиоиды:
?
Второй вопрос – о выпуклости кривой.
Для получения ответов на эти вопросы
рассмотрим параметрические уравнения
части кардиоиды: ,
, .
.
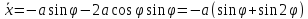 ,
,
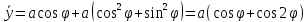 .
.
Из
уравнения
 при
при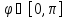 ,
находим
,
находим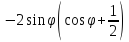 ,
,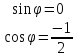 ,
откуда
,
откуда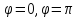 ,
,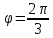 .
Этим значениям соответствуют
.
Этим значениям соответствуют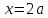 (при
(при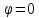 ),
),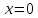 (при
(при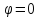 ),
абсцисс 0.
),
абсцисс 0.
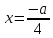 (при
(при
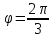 )
- абсцисса точки
)
- абсцисса точки .
.
Таким
образом, на вопрос об абсциссе точки
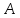 получим ответ
получим ответ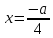 .
.
Производная
 .
.
Отметим,
что в точках
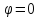 ,
, кривая имеет вертикальную касательную.
кривая имеет вертикальную касательную.
Вторая
производная равна
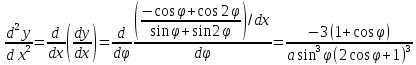 .
.
На
промежутке
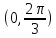 эта величина меньше 0, на промежутке
эта величина меньше 0, на промежутке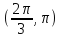 - больше 0.
- больше 0.
Поэтому
верхняя половина кардиоиды состоит из
выгнутой вверх кривой, соединяющей
точки
 и
и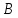 и
выгнутой вниз кривой, соединяющей точки
и
выгнутой вниз кривой, соединяющей точки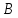 и
и .
.
