
- •§1.Схема построения графиков
- •§2.Преобразования графиков
- •§3. Графики основных элементарных функций
- •3.1. Степенная функция
- •3.2. Показательная функция
- •3.3 Логарифмическая функция
- •3.4 Тригонометрические функции
- •3.5 Обратные тригонометрические функции
- •§4. Построение кривых, заданных параметрически
- •§5. Построение кривых, заданных уравнением в полярных координатах.
3.2. Показательная функция
Показательная
функция
 ,
, определена при всех
определена при всех и принимает положительные значения.
Она непрерывна на всей прямой. Если
и принимает положительные значения.
Она непрерывна на всей прямой. Если ,
то
,
то ,
а если
,
а если ,
то
,
то .
Её производная равна
.
Её производная равна .
Эта величина меньше
.
Эта величина меньше для всех
для всех ,
если
,
если .
При этом функция возрастает. Если же
.
При этом функция возрастает. Если же ,
то производная
,
то производная для всех
для всех ,
функция убывает. Её вторая производная
,
функция убывает. Её вторая производная для всех
для всех и всех
и всех .
Поэтому график выгнут вниз. На рисунке
изображены графики
.
Поэтому график выгнут вниз. На рисунке
изображены графики при
при и
и ,
соответственно.
,
соответственно.
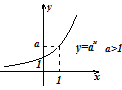

3.3 Логарифмическая функция
Логарифмическая
функция
 является обратной для показательной
функции, т.е.
является обратной для показательной
функции, т.е. для всех
для всех .
.
Областью
определения логарифмической функции
является множество
 .
Разумеется, показательная функция тоже
является обратной функцией для
логарифмической, однако
.
Разумеется, показательная функция тоже
является обратной функцией для
логарифмической, однако только
при
только
при .
.
Логарифмическая функция непрерывна в своей области определения.

Поэтому
ее график имеет вертикальную асимптоту
 .
Производная
.
Производная положительная при
положительная при ,
если
,
если и отрицательна, если
и отрицательна, если .
Поэтому при
.
Поэтому при функция возрастает, при
функция возрастает, при убывает. Множество ее значений:
убывает. Множество ее значений: .
Вторая производная
.
Вторая производная отрицательна при
отрицательна при и положительна, если
и положительна, если .
Поэтому в первом случае график выгнут
вверх, а во втором случае – вниз.
Разумеется, график этой функции
симметричен графику соответствующей
показательной функции относительно
биссектрисы первого и третьего
координатных углов.
.
Поэтому в первом случае график выгнут
вверх, а во втором случае – вниз.
Разумеется, график этой функции
симметричен графику соответствующей
показательной функции относительно
биссектрисы первого и третьего
координатных углов.


3.4 Тригонометрические функции
Функция
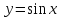 .
.
Эта
функция определена и непрерывна на
 ,
является нечетной и периодической с
наименьшим положительным периодом
,
является нечетной и периодической с
наименьшим положительным периодом .При
стремлении
.При
стремлении к
к предела этой функции нет.
предела этой функции нет.
Её
производная
 .
Эта величина положительна при
.
Эта величина положительна при на них
на них возрастает, и отрицательна при
возрастает, и отрицательна при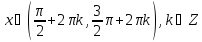 ,
где функция убывает. В точках
,
где функция убывает. В точках функция имеет локальные максимумы, а в
точках
функция имеет локальные максимумы, а в
точках - локальные минимумы. Соответствующие
значения равны 1 и -1. Поэтому множеством
значений является отрезок
- локальные минимумы. Соответствующие
значения равны 1 и -1. Поэтому множеством
значений является отрезок .
Наконец,
.
Наконец, ,
поэтому
,
поэтому ,
если
,
если ,
где график выгнут вниз, и
,
где график выгнут вниз, и ,
если
,
если ,
где график выгнут вверх.
,
где график выгнут вверх.

Функция
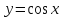 .
.
Ввиду
равенства
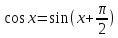 ,
график функции
,
график функции получается из графика функции
получается из графика функции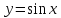 сдвигом по оси
сдвигом по оси влево на
влево на .
.

Функция

Она
определена при
 ,
т.к.
,
т.к.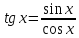 .
В области определения она является
непрерывной. График имеет вертикальные
асимптоты в точках
.
В области определения она является
непрерывной. График имеет вертикальные
асимптоты в точках ,
причем
,
причем ,
, .
Функция нечётная, т.к.
.
Функция нечётная, т.к. .
Это периодическая функция с наименьшим
положительным периодом
.
Это периодическая функция с наименьшим
положительным периодом .
Так как
.
Так как в области определения,
в области определения, строго возрастает на каждом интервале
строго возрастает на каждом интервале .
Её множество значений совпадает с
.
Её множество значений совпадает с .
. ,
при
,
при график выгнут вверх, при
график выгнут вверх, при - выгнут вниз. В точках
- выгнут вниз. В точках - перегибы.
- перегибы.
График
функции
 .
.
Этот
график легко построить, используя
равенство
 .
.

3.5 Обратные тригонометрические функции
График
функции
 .
.
Функция
определена и непрерывна на отрезке
 .
Она является нечетной. Так как
.
Она является нечетной. Так как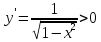 для всех
для всех ,
функция возрастает. Множество её значений
– отрезок
,
функция возрастает. Множество её значений
– отрезок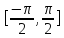 .
Вторая производная
.
Вторая производная .
При
.
При выполняется неравенство
выполняется неравенство ,
график выгнут вниз, при
,
график выгнут вниз, при -
- ,
график выгнут вверх. Точка
,
график выгнут вверх. Точка -
точка перегиба. График имеет вид:
-
точка перегиба. График имеет вид:

График
функции
 можно построить из графика функции
можно построить из графика функции ,
используя формулу
,
используя формулу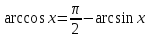 .
.

Функция
 определена и непрерывна на всей числовой
прямой.
определена и непрерывна на всей числовой
прямой. ,
, ,
поэтому график имеет горизонтальные
асимптоты. Функция нечетная. Производная
,
поэтому график имеет горизонтальные
асимптоты. Функция нечетная. Производная ,
функция возрастает. Её множество значений
- интервал
,
функция возрастает. Её множество значений
- интервал .
Вторая производная равна
.
Вторая производная равна Она
положительна при
Она
положительна при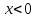 и отрицательна при
и отрицательна при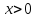 .
При
.
При график выгнут вниз, при
график выгнут вниз, при - выгнут вверх. Точка
- выгнут вверх. Точка – точка перегиба.
– точка перегиба.

График
функции
 получается
из этого графика по формуле
получается
из этого графика по формуле .
.
