
- •§1.Схема построения графиков
- •§2.Преобразования графиков
- •§3. Графики основных элементарных функций
- •3.1. Степенная функция
- •3.2. Показательная функция
- •3.3 Логарифмическая функция
- •3.4 Тригонометрические функции
- •3.5 Обратные тригонометрические функции
- •§4. Построение кривых, заданных параметрически
- •§5. Построение кривых, заданных уравнением в полярных координатах.
§1.Схема построения графиков
Имеется
несколько способов задавать зависимость
между переменными
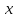 и
и
 .
Чаще всего используется явное выражение
.
Чаще всего используется явное выражение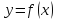 .
Можно считать
.
Можно считать и
и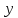 функциями от параметра:
функциями от параметра: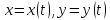 .
Можно задать эту зависимость в виде
уравнения
.
Можно задать эту зависимость в виде
уравнения .
В последнем случае говорят о неявно
заданной функции.
.
В последнем случае говорят о неявно
заданной функции.
Графическое изображение функциональной зависимости позволяет наглядно представить свойства изучаемой функции.
Опишем
схему построения графика функции,
заданного явным уравнением
 .
Напомним, что график этой функции
представляет собой множество точек на
плоскости, координаты которых
.
Напомним, что график этой функции
представляет собой множество точек на
плоскости, координаты которых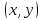 связаны равенством
связаны равенством .
.
При
исследовании функции следует начинать
с нахождения области определения этой
функции. Обычно, когда ставится задача
построить график функции
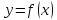 ,
рассматривается естественная область
определения, т.е. множество чисел
,
рассматривается естественная область
определения, т.е. множество чисел ,
при которых определено выражение
,
при которых определено выражение .
В ряде случаев рассматривается часть
области определения, обозначим эту
часть
.
В ряде случаев рассматривается часть
области определения, обозначим эту
часть .
Тогда мы говорим об ограничении функции
.
Тогда мы говорим об ограничении функции на множество
на множество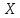 .
.
Ограничения
функции
 на различные подмножества
на различные подмножества и
и могут обладать разными свойствами.
Например, ограничение функции
могут обладать разными свойствами.
Например, ограничение функции на множество
на множество – убывающая функция, а ограничение
– убывающая функция, а ограничение – возрастающая функция.
– возрастающая функция.
После нахождения области определения функции, исследуем её на непрерывность и выясняем её асимптотическое поведение при стремлении к бесконечно удалённым точкам, или к граничным точкам области определения.
Некоторые
функции обладают специфическими
свойствами. Напомним, что функция
 называетсячётной,
если она определена на симметричном
относительно точки
называетсячётной,
если она определена на симметричном
относительно точки
 множестве
множестве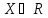 и если для любого
и если для любого выполняется равенство
выполняется равенство .
График чётной функции симметричен
относительно оси
.
График чётной функции симметричен
относительно оси .Нечётной
называется функция
.Нечётной
называется функция
 ,
если она определена на симметричном
относительно точки
,
если она определена на симметричном
относительно точки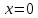 множестве
множестве и если для любого
и если для любого имеет место равенство
имеет место равенство .
График нечётной функции симметричен
относительно начала координат. Функция
называетсяпериодической,
если существует число
.
График нечётной функции симметричен
относительно начала координат. Функция
называетсяпериодической,
если существует число
 такое, что для любого
такое, что для любого – области определения функции
– области определения функции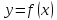 числа
числа также принадлежат
также принадлежат и
и .
.
Далее
вычисляем производную
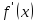 и исследуем её знак. На множестве, где
и исследуем её знак. На множестве, где ,
функция
,
функция возрастает, на множествах, где
возрастает, на множествах, где ,
функция
,
функция убывает. Экстремумы функция может иметь
в тех точках, где либо
убывает. Экстремумы функция может иметь
в тех точках, где либо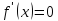 ,
либо
,
либо не существует. Нахождение наибольшего
или наименьшего значений функции, если
они есть, позволяет установить множество
не существует. Нахождение наибольшего
или наименьшего значений функции, если
они есть, позволяет установить множество значений, принимаемых функцией.
значений, принимаемых функцией.
Исследование
знака второй производной
 позволяет установить промежутки, на
которых график функции выпукл вверх,
или выпукл вниз, а также точки перегиба.
позволяет установить промежутки, на
которых график функции выпукл вверх,
или выпукл вниз, а также точки перегиба.
§2.Преобразования графиков
Пусть
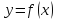 определена на множестве
определена на множестве
 ,
возрастает на
,
возрастает на (или убывает на
(или убывает на )
и пусть
)
и пусть – множество значений этой функции.
Тогда для любого
– множество значений этой функции.
Тогда для любого существует единственное значение
существует единственное значение такое, что
такое, что .
Это
.
Это обозначим так:
обозначим так: .
Обратной для
.
Обратной для функцией назовём функцию
функцией назовём функцию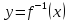 .
Для всех
.
Для всех выполнено равенство
выполнено равенство .
Для всех
.
Для всех выполнено равенство
выполнено равенство .
Например для
.
Например для имеем:
имеем: ,
,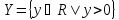 .
Поэтому для всех
.
Поэтому для всех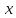
 и для всех
и для всех
 .
.
График
обратной функции симметричен графику
функции
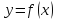 относительно биссектрисы координатного
угла.
относительно биссектрисы координатного
угла.
Термины
“сложная функция”, или “композиция
функций” (а также “суперпозиция
функций”) относятся к способу представления
функции. Если, например,
 и
и определена на множестве значений
определена на множестве значений ,
принимаемых функцией
,
принимаемых функцией ,
то говорят, что
,
то говорят, что – сложная функция, или композиция этих
функций.
– сложная функция, или композиция этих
функций.
Особенно
часто рассматриваются сложные функции
вида
 .
.
Так
как
 ,
точки
,
точки графика
графика ,
для которых
,
для которых ,
одновременно являются и точками графика
,
одновременно являются и точками графика .
Те точки
.
Те точки графика
графика ,
для которых
,
для которых ,
при построении графика
,
при построении графика заменяются точками
заменяются точками ,
т.е. точками симметричными относительно
оси
,
т.е. точками симметричными относительно
оси .
.


При
построении графика функции
 сохраняем точки
сохраняем точки графика функции
графика функции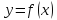 для которых
для которых ,
а потом
,
а потом соответствуют значения
соответствуют значения ,
т.е. график
,
т.е. график получается симметричным относительно
оси
получается симметричным относительно
оси отражением графика ограничения на
множество
отражением графика ограничения на
множество функции
функции .
.

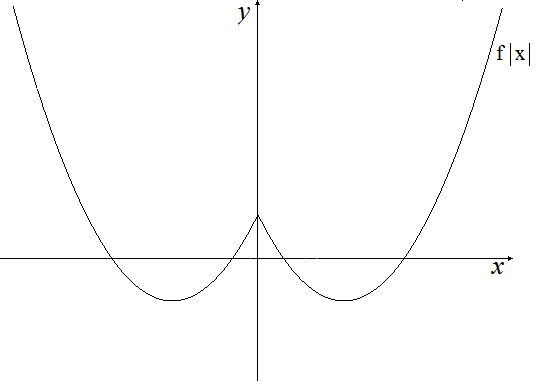
Перейдём
к построению графиков вида
 и начнём с рассмотрения важных частных
случаев.
и начнём с рассмотрения важных частных
случаев.
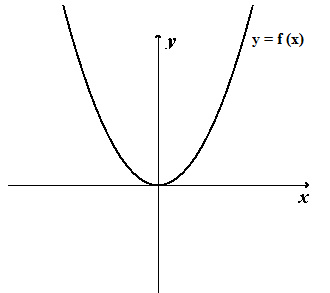
График
функции
 получается из графика функции
получается из графика функции сдвигом на число
сдвигом на число по оси
по оси :
:


График
функции
 получается из графика функции
получается из графика функции сдвигом на число
сдвигом на число по оси
по оси

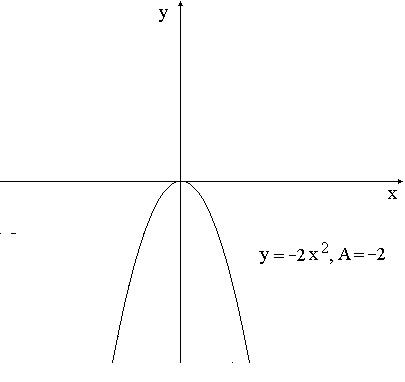
График
функции
 получается из графика
получается из графика умножением координаты
умножением координаты на число
на число


График
 получается из графика
получается из графика при
при сжатием вдоль оси
сжатием вдоль оси в
в раз, если
раз, если и растяжением в
и растяжением в раз, если
раз, если .
.
Если
же
 ,
то для построения графика
,
то для построения графика следует построить график
следует построить график согласно указанному выше правилу, затем
отразить полученный график симметрично
относительно оси
согласно указанному выше правилу, затем
отразить полученный график симметрично
относительно оси .
.


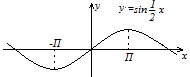

Для
получения графика функции
 следует представить её в виде
следует представить её в виде и последовательно использовать
приведённые выше правила.
и последовательно использовать
приведённые выше правила.
