
- •1. Определение задачи математического программирования
- •2. Допустимое решение задачи, одр, оптимальное решение задачи.
- •3. Экономико–математические модели задач лп: задача о банке
- •Задача о банке
- •4. Экономико – математические модели задач лп: задача определения оптимального ассортимента продукции.
- •5. Задача лп, стандартная форма, каноническая форма.
- •6. Целевая функция, градиент
- •7. Двойственная задача и ее свойства
- •8. Первая теорема двойственности и ее следствия
- •94. Экономическая интерпретация двойственной задачи.
- •10. Транспортная задача, математическая модель и ее свойства.
- •11. Метод минимального элемента, метод северо-западного угла.
- •12. Метод потенциала, цикл
- •13.Открытые модели транс-ой задачи.Принцип замыкания
- •14. Матричные игры с нулевой суммой.
- •15. Смешанные стратегии, чистые стратегии.
- •16. Оптим-ое решение игры в смешанных стратегиях, седловая точка
- •21. Кооперативная игра, коалиции и дележи.
- •24 Альтернатива (альтернативная стратегия)
- •28. Риск, источники риска.
- •26. Динамическое программирование.
- •27. Метод дп включает три основных этапа:
- •29. Полнота и арбитраж.
- •30. Модель (b,s) – рынка. Пример дискретной и непрерывной модели.
- •31. Хеджирование как метод защиты от риска.
- •32. Модель Марковица.
- •33. Общие сведения о сетях
- •34 Сетевое планирование и управление
- •35. Временные параметры сетевых моделей
- •36.Сетевые графики и их анализ
- •37. Однофакторное и многофакторное уравнения регрессии
- •38. Типы связи между случайными величинами.
- •39. Коэффициент корреляции, детерминации.
- •Вопрос 16. Метод северо-западного угла
- •Вопрос 17. Метод потенциалов
11. Метод минимального элемента, метод северо-западного угла.
Выбрали клетку с координатами (i j) – свободная северо – запад.
 то
то
 ставим прочерки во всех свободных
клеткахi
строки.
ставим прочерки во всех свободных
клеткахi
строки.
 то
то
 ставим прочерки во всех свободных
клеткахj
столбца.
ставим прочерки во всех свободных
клеткахj
столбца.
 то
то
 ставим прочерки во всех свободных
клеткахi
строки или j
столбца.
ставим прочерки во всех свободных
клеткахi
строки или j
столбца.
Пересчитываем:


До тех пор пока везде не будут числа или прочерки. Клетки, в которых числа – базисные. Клетки с прочерками – не базисные. Кол-во базисных = m+n-1.
Метод минимального
Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку, которая ей соответствует, помещают меньшее из чисел и . Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
12. Метод потенциала, цикл
Пусть
каждый из пунктов производства продукции
вносит за перевозку единицы груза
какую-то сумму
 ; в свою очередь, каждый из пунктов
потребления также вносит за перевозку
единицы груза сумму
; в свою очередь, каждый из пунктов
потребления также вносит за перевозку
единицы груза сумму ; эти платежи передаются некоторому
третьему лицу («перевозчику»).
; эти платежи передаются некоторому
третьему лицу («перевозчику»).
Перевозка
единицы груза из i-го в j-ый пункт
объективно стоит
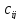 ,
а стороны вместе платят за эту перевозку
«перевозчику» сумму:
,
а стороны вместе платят за эту перевозку
«перевозчику» сумму:
Величина
 называется «псевдостоимостью» перевозки
единицы груза из i-го пункта производства
в j-ый пункт потребления.
называется «псевдостоимостью» перевозки
единицы груза из i-го пункта производства
в j-ый пункт потребления.
Платежи и не обязательно должны быть положительными/
Оптимальным будет такой план перевозок, при котором пункты i и j не переплачивают «перевозчику» ничего сверх объективной стоимости перевозок .
Цикл – последовательный набор клеток, в котором любые 2 клетки находятся в одной строке или столбце таблицы. И никакие 3 соседние клетки не находятся в одной строке или столбце. Первая и последняя клетка цикла должна быть из одной строки или столбца.
13.Открытые модели транс-ой задачи.Принцип замыкания
Транспортная
задача, в которой суммарные запасы и
потребности совпадают, т. е. выполняется
условие
 называетсязакрытой
моделью;
в противном случае – открытой. Для
открытой модели может быть два случая:
называетсязакрытой
моделью;
в противном случае – открытой. Для
открытой модели может быть два случая:
а)
суммарные запасы превышают суммарные
потребности:

б)
суммарные потребности превышают
суммарные запасы:

Открытая
модель ТЗ решается приведением к
закрытой модели. В случае (а), когда
суммарные запасы превышают сум-ые
потребности, вводится фиктивный
потребитель (столбец Вn+1), потребности
которого
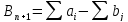 .
В случае (б), когда суммарные потр-сти
превышают суммарные запасы, вводится
фиктивный поставщик (строка Am+1), запасы
которого
.
В случае (б), когда суммарные потр-сти
превышают суммарные запасы, вводится
фиктивный поставщик (строка Am+1), запасы
которого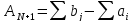 .
.
.
.
Стоимость перевозки единицы груза, как до фиктивного потребителя, так и стоимость перевозки единицы груза от фик-го поставщика полагают равными нулю, так как груз в обоих случаях не перевозится. После преобразований задача принимает вид закрытой модели и решается обычным способом.
