- •Тема 1. Основы классической логики
- •Тема 2. Отношения между понятиями, суждениями. Умозаключение из суждений с отношениями
- •Тема 3. Классы и множества. Логические отношения между классами (множествами). Связь между бинарными отношениями и двуместными предикатами
- •Тема 4. Комбинаторные методы решения логических задач
- •Тема 5. Формализация бинарных отношений и двуместных предикатов в виде графов
- •X1 x2 x1 x1 x2 x1
- •Тема 6. Повторение и закрепление пройденного материала.
- •5.Оценочные средства для текущего контроля успеваемости, промежуточной и итоговой аттестации по дисциплине
- •Контрольное задание
- •6. Учебно-методическое и информационное обеспечение учебной дисциплины
Тема 3. Классы и множества. Логические отношения между классами (множествами). Связь между бинарными отношениями и двуместными предикатами
Занятие 1
Повторение определений основных понятий темы.
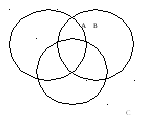
Подберите понятия, отношения между которыми можно изобразите
к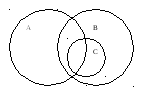 ругами
Эйлера следующим образом:
ругами
Эйлера следующим образом:


 на дом
на дом
Правильно ли определены отношения между понятиями?
А -четырехугольник;
-четырехугольник;
В-трапеция;
С-равнобедренная трапеция;
D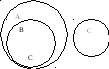 -квадрат.
-квадрат.
на дом
А-река;
В-судоходная река;
С-исток реки.
Определите вид суждения, его субъект и предикат. Выразите
отношения с помощью кругов Эйлера.
Все трапеции-четырехугольники.
Многие люди застенчивы.
Некоторые спортсмены не являются олимпийскими чемпионами.
Все сказуемые являются главными членами предложения.
Константин Симонов – автор романа «Живые и мертвые».
Иногда люди проявляют нетерпимость.
Некоторые учащиеся не изучают логику.
Некоторые растения являются лекарственными.
на дом
Ни один георгин не имеет шипов.
Понедельник – первый день недели.
Юрий Гагарин – первый космонавт.
Некоторые летчики не являются летчиками-космонавтами.
Занятие 2
Повторение определений основных понятий темы.
На плоскости
 задан предикат
задан предикат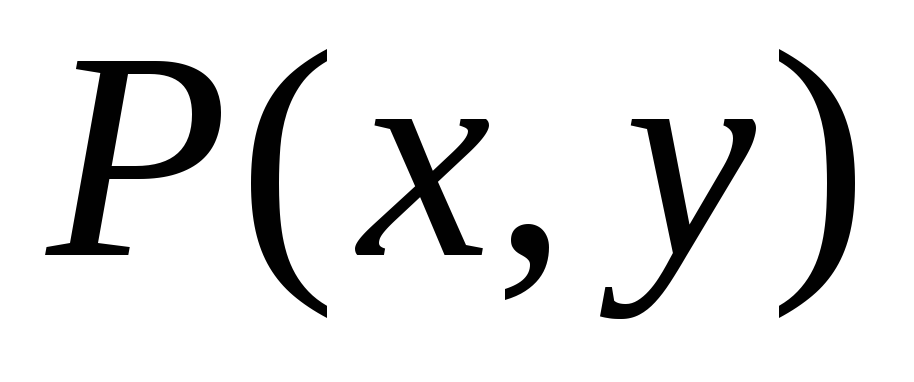 ,
множеством истинности которого является
область, граница которой состоит из
прямых отрезков, соединяющих
последовательно точки с координатами
(0, 0), (3, 0), (3, 2), (2, 2), (2, 1),
(0, 1), (0, 0).
,
множеством истинности которого является
область, граница которой состоит из
прямых отрезков, соединяющих
последовательно точки с координатами
(0, 0), (3, 0), (3, 2), (2, 2), (2, 1),
(0, 1), (0, 0).
Множества
истинности предикатов
![]() определяются множествами точек
определяются множествами точек![]() и
и![]() соответственно на плоскости
соответственно на плоскости![]() ,
где
,
где![]() – действительные числа.
– действительные числа.
Используя
операции над множествами, записать
формулу получения множества истинности
предиката
![]() .
.
на дом
На
плоскости
![]() задан предикат
задан предикат![]() ,
множеством истинности которого является
область, граница которой состоит из
прямых отрезков, соединяющих последовательно
точки с координатами (0, 0), (0, 2),
(2, 2), (2, 1), (1, 1), (1, 0), (0, 0).
,
множеством истинности которого является
область, граница которой состоит из
прямых отрезков, соединяющих последовательно
точки с координатами (0, 0), (0, 2),
(2, 2), (2, 1), (1, 1), (1, 0), (0, 0).
Множества
истинности предикатов
![]() определяются множествами точек
определяются множествами точек![]() и
и![]() соответственно на плоскости
соответственно на плоскости![]() ,
где
,
где![]() – действительные числа.
– действительные числа.
Используя
операции над множествами, записать
формулу получения множества истинности
предиката
![]() .
.
Даны множества: I= {1, 2, 3, 4, 5}, X={1, 5}, Y={1, 2, 4}, Z={2, 5}. Найти следующие множества и начертить круги Эйлера, иллюстрирующие их построение,
а)
![]() б)
б)
![]()
на дом
а)
![]() б)
б)
![]()
Доказать с помощью кругов Эйлера следующие тождества
![]()
на дом
![]() .
.
5. Даны множества: X={1, 5}, Y={1, 2, 4}, Z={2, 5}.
Найти следующие множества и начертить координатные диаграммы, иллюстрирующие их построение,
а)
![]() , б)
, б)
![]() ,
,
Проверить выполнение свойств коммутативности (пример а) и дистрибутивности (пример б) операции прямого произведения.
на дом
![]() .
.
Занятие 3
Повторение определений основных понятий темы.
Выписать все элементы отношений =<X, R> и -1 и представить их в виде координатных диаграмм, если
а) X= {1, 3, 5}, R = {<x, y>: x y},
б) X={2, 4, 16, 22}, R ={<x, y>: x является делителем y},
на дом
а) ![]() .
.
3. Нарисовать графы отношений.
а) X= {1, 3, 5}, R = {<x, y>: x y},
б) X= {2, 4, 16, 22}, R ={<x, y>: x является делителем y},
на дом
а) ![]() .
.
4. Исследовать свойства отношений, приведенных в п. 2, (рефлексивность, симметричность, транзитивность, антисимметричность, иррефлексивность, асимметричность, сравнимость). Определить, являются ли эти отношения а) отношением эквивалентности; б) отношением строгого порядка; в) отношением нестрогого порядка; г) отношением линейного порядка.
5. Пусть X = Y = R ,где R-множество действительных чисел, а отображение : X Y задается указанным ниже законом. Нарисовать график отображения и охарактеризовать отображение (всюду определенность, функциональность, отображение “на”, взаимная однозначность).
а) y = | x | , б) | y | = | x |
на дом
а) x = y2 ; б) y = tg x.