
- •Введение
- •1.Общие положения
- •1.1.Тематика курсовых работ
- •1.2.Расчетная часть
- •2. Порядок выполнения расчетов
- •2.2. Построение статистического ряда
- •2.3. Определение оценок числовых характеристик
- •2.4. ИСКЛЮЧЕНИЕ ИЗ МАССИВА ПРОМАХОВ
- •2.5 Определение закона распределения вероятности экспериментальных данных
- •2.5.1. Построение гистограммы
- •2.5.2. Аппроксимация гистограммы и определение аналитического выражения функции плотности распределения вероятности
- •2.6.1. Основные теоретические положения применения критериев согласия при проверке гипотез
- •2.6.3. Критерий согласия А.Н. Колмогорова
- •2.6.4 Критерий согласия К. Пирсона (критерий χ2)
- •2.7.1. Общие сведения о характеристиках положения закона распределения вероятности и их оценках
- •2.7.2. Определение оценки характеристики положения
- •2.7.3. Представление результата измерения
- •Приложение А
- •Приложение Б

|
1 |
|
|
|
|
|
График 3 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
0,9 |
|
|
|
|
|
|
|
|
|
Вероятность |
0,8 |
|
|
|
|
|
|
|
|
|
0,7 |
|
|
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 11 12 13 14 15 |
|
|
|
|
|
Номера интервалов |
|||||
2.5.2. Аппроксимация гистограммы и определение аналитического выражения функции плотности распределения вероятности
Для определения аналитического выражения аппроксимирующей функции плотности распределения вероятности необходимо сгладить полученный на основе гистограммы полигон распределений, представив его в виде более плавной кривой, после чего сравнить полученную экспериментальную кривую с теоретическими кривыми плотностей распределения вероятности различных законов. Ряд ЗРВ приведены в данном пособии. Другие законы могут быть получены студентом самостоятельно из справочного материала или из перечисленных литературных источников. Так как очень часто по внешнему виду один закон распределения вероятности трудно отличить от другого, а некоторые из них при определенных значениях параметров переходят друг в друга, то после определения аналитического выражения аппроксимирующей функции плотности распределения вероятности следует провести сравнение оценок начальных и центральных моментов, полученных в п. 2.2 (стандартное отклонение, оценки ассиметрии, эксцесса и т.д.), с теоретическими, приведенными в табл. 2, 3 и 6.
При подборе аппроксимирующей функции плотности распределения вероятности необходимо учитывать, что

-в некоторых случаях для более точной аппроксимации необходимо применить сумму двух или более функций;
-в связи с тем, что некоторые распределения по внешнему виду похожи друг на друга, целесообразно для дальнейшего анализа выбрать не одну аппроксимирующую функцию, а две или более;
-аналитические выражения аппроксимирующих функций могут быть представлены в виде уравнений прямых (или суммы прямых),
экспонент (суммы экспонент) и других функций.
После выбора аналитического выражения аппроксимирующей функции плотности вероятности необходимо определить параметры функции (т.е. коэффициенты, входящие в аналитическое выражение), если вычисленных моментов
Таблица 6
|
|
|
|
|
|
|
|
|
Критериальные значения |
||
|
|
|
|
|
|
|
|
Наименование |
характеристик |
||
|
|
|
|
|
|
|
|
распределения |
|||
Вид |
|
|
|
|
|
|
|
функции |
|||
|
|
|
|
|
|
|
Коэффи- |
Коэффи- |
|
||
функ- |
|
График функции |
распределения |
|
|||||||
ции |
|
|
|
|
|
|
|
(плотности |
циент |
циент |
Контр- |
|
|
|
|
|
|
|
|
вероятностей) |
асим- |
эксцесса |
эксцесс |
|
|
|
|
|
|
|
|
|
мет- |
µ4/ SQ4 -3 |
|
|
|
|
|
|
|
|
|
|
рии |
|
|
1 |
2 |
|
|
|
3 |
4 |
5 |
6 |
|||
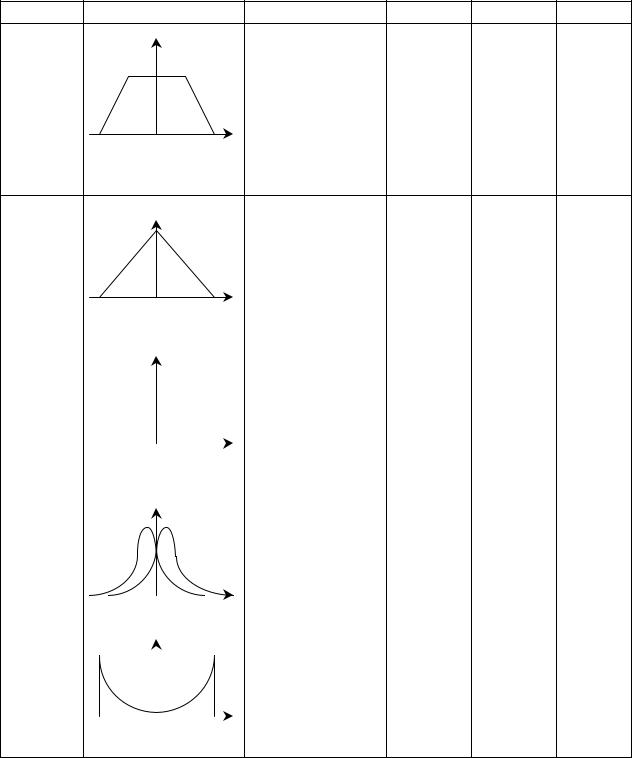
Одно- |
|
|
|
f(Q) |
|
|
|
Симметричная |
|
|
|
мо- |
|
|
|
|
|
|
экспонен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
дальная |
|
|
|
|
|
|
|
циальная для |
|
|
|
симмет- |
|
|
|
|
|
|
|
значений |
|
|
|
ричная |
|
|
|
|
|
|
|
степени |
|
|
|
остро- |
|
|
|
|
|
|
|
0,5 |
0 |
22 |
0,199 |
вершин- |
0 |
Q |
0,7 |
0 |
8 |
0,304 |
|||||
ная |
1,0 |
0 |
3 |
0,408 |
|||||||
|
|
|
|
|
|
|
|
1,5 |
0 |
0,75 |
0,517 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(Q) |
|
|
|
|
|
|
|
Одномо |
|
|
|
|
|
|
|
|
|
|
|
дальная |
|
|
|
|
|
|
|
Нормальная |
0 |
0 |
0,577 |
симмет- |
|
|
|
|
|
|
|
||||
ричная |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
Q |
|
|
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
Окончание табл. 6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
Одно- |
|
f(Q) |
|
|
|
мо- |
|
|
|
|
|
дальная |
|
|
|
|
|
симмет- |
|
Трапецеидаль- |
|
0 – |
0,58 – |
ричная |
|
0 |
|||
|
ная |
(-1,2) |
0,74 |
||
плоско- |
|
|
|||
0 |
Q |
|
|
|
|
вершин- |
|
|
|
||
ная |
|
f(Q) |
|
|
|
Одномо |
|
|
|
|
|
дальная |
|
|
|
|
|
симмет- |
|
|
|
|
|
ричная |
|
Треугольная |
0 |
- 0,6 |
0,646 |
|
|
||||
|
-a |
0 |
|
a |
Q |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(Q) |
|
|
|
|
|
Безмо- |
|
|
|
|
|
Равномерная |
0 |
-1,2 |
0,745 |
|
|
|
|
|
|
||||||
дальная |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
-a |
0 |
a |
Q |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Одно- |
|
|
f(Q) |
|
|
|
|
|
||
мо- |
|
|
|
|
Ряд Грама – |
|
|
|
||
дальная |
|
|
|
|
-1,0 – |
-1,2 – |
0,4 – |
|||
асимет- |
|
|
|
|
Шарлье |
|||||
|
|
|
|
1,0 |
3 |
0,74 |
||||
ричная |
|
|
|
|
|
|
|
|||
|
0 |
|
Q |
|
|
|
||||
|
|
|
|
|
|
|
||||
Анти- |
|
|
f(Q) |
|
|
|
|
|
||
модаль- |
|
|
|
|
Арксинусои- |
|
|
|
||
ная |
|
|
|
|
|
|
|
|||
симмет- |
|
|
|
|
|
дальная |
0 |
- 1,5 |
0,816 |
|
ричная |
|
0 |
|
Q |
|
|
|
|||
недостаточно. Параметры некоторых функций (например, равномерное распределение вероятности, треугольное, трапецеидальное и т.д.) определяются легко с помощью полученной экспериментальной кривой, другие (например, нормальное распределение, распределение Максвелла,

Релея и т.д.) не требуют дополнительных вычислений, так как полученных значений среднего арифметического и стандартного отклонения достаточно для определения всех констант, входящих в аналитическое выражение функции плотности вероятности. Однако есть более сложные выражения аналитических функций плотности вероятности (например, распределения Накагами, Пирсона, Стъюдента и т.д.), которые требуют нахождения определенного параметра, и вид функции зависит от значения этого параметра. В этом случае может быть рекомендована только процедура вычисления аппроксимирующей функции при различных значениях неизвестного параметра с последующим ее наложением на гистограмму.
При выборе параметров необходимо учитывать, что интеграл от
аналитического выражения функции плотности вероятности в бесконечных пределах (или в пределах изменения значений экспериментальных данных) должен быть равен единице или близок к ней. Это условие может быть основным и при подборе параметров выражения аппроксимируюшей функции.
ПРИМЕР. В приведенном выше примере получены 3 вида гистограмм, при этом можно считать, что 2-я и 3-я гистограммы близки по форме к друг другу и к двухмодальному распределению, а первая
– к трапецеидальному. Для дальнейшего анализа в качестве примера рассмотрим гистограммы 1 и 3, с помощью которых построим экспериментальные полигоны распределения и аппроксимирующие кривые плотности распределения вероятности. Для первой гистограммы подберем аппроксимирующую кривую в виде трапецеидального ЗРВ, а для третьй - двухмодальный экспоненциальный.
Значения экспериментальной вероятности попадания отсчета в
N
интервал в зависимости от Q определяются величиной n×∆Q .
Полученные результаты относятся к середине интервала и записываются в таблицу. Если соединить эти значения на гистограмме отрезками прямой, то получаем полигон распределения, построенный вместе с гистограммами. Значения теоретической плотности распределения вероятности получаются по теоретической зависимости, которая должна быть близка по форме к экспериментально полученному полигону
иописываться аппроксимирующим аналитическим выражением.
1.Определение аналитического выражения функции плотности распределения вероятности по гистограмме 1.
Представим аналитическое выражение аппроксимирующей функции в следующем виде:
|
0 при −∞ ≤ Q ≤ Q1 |
|
|
|
|
|||
|
аQ −в при Q |
≤ Q ≤ Q |
2 |
|
|
|||
|
|
|
1 |
|
|
|
|
|
Р1 (Q) = |
|
при Q2 |
≤ Q |
≤ Q3 |
|
|
|
(20) |
с |
|
|
|
|||||
|
− аQ + g при Q ≤ |
Q ≤ Q |
|
|
||||
|
|
|
|
3 |
|
4 |
|
|
|
|
при Q4 |
≤ Q |
≤ +∞ |
|
|
|
|
|
0 |
|
|
|
|
|||
Значения параметров ( а,в,с и g), входящих в аналитическое выражение, можно найти с помощью гистограммы 1.
Параметр с определим как среднее арифметическое экспериментального полигона распределения вероятности при Q = 3,375; Q = 4,2; Q = 5,025. Эта величина приблизительно равна с ≈ 0,362. Значения а,в и g находим из условий:
1)при Q = 3,375 значение Р1(Q) = 0,362,
2)при Q = 2,55 и Q = 5,85 значение Р1(Q) равно среднему арифметическому экспериментального полигона распределения вероятности при Q = 2,55 и Q = 5,85 (эта величина равна 0,06315).
После расчетов получено, что а = 0,36224, в = 0,86057, g = 2,18226. С
помощью найденных параметров а,в,с и g определены значения теоретической плотности распределения вероятности, которые записаны в табл. 7 и представлены в виде графиков на рис. 2. Проверку правильности расчетов целесообразно провести исходя из двух условий:
-средние арифметические значения экспериментальной и аппроксимирующей кривых должны быть равны;
-площадь под аппроксимирующей кривой должна быть близка к единице.
|
|
|
|
Таблица 7 |
|
|
Средние |
|
|
|
|
|
|
значения |
2,55 |
3,375 |
4,2 |
|
5,025 |
5,85 |
интервалов Q |
|
|
|
|
|
|
Рэкс(Q) |
0,0707 |
0,394 |
0,2677 |
|
0,4242 |
0,0556 |
Р1(Q) |
0,06315 |
0,362 |
0,362 |
|
0,362 |
0,06315 |
Р2(Q)×∆N |
0,0521 |
0,29865 |
0,29865 |
|
0,29865 |
0,0521 |


 Рэкс(Q)
Рэкс(Q) 
 Р1(Q)
Р1(Q)
|
0,45 |
|
|
|
|
|
0,4 |
|
|
|
|
Вероятность |
0,35 |
|
|
|
|
0,3 |
|
|
|
|
|
0,25 |
|
|
|
|
|
0,2 |
|
|
|
|
|
0,15 |
|
|
|
|
|
|
0,1 |
|
|
|
|
|
0,05 |
|
|
|
|
|
0 |
|
|
|
|
|
2,55 |
3,375 |
4,2 |
5,025 |
5,85 |
|
|
Средние значения интервалов |
|
||
Рис. 2. Экспериментальный полигон распределения и аппроксимирующая функция плотности (для гистограммы 1)
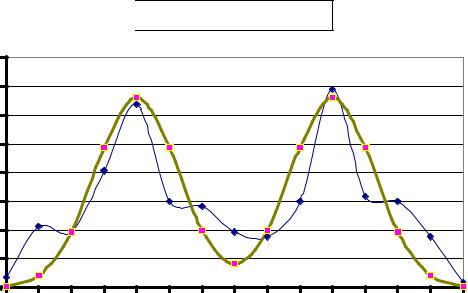
2.Определение аналитического выражения функции плотности распределения вероятности по гистограмме 3.
Экспериментальные значения полигона распределения вероятности получаем с помощью табл. 5 соединяя на гистограмме 3 середины интервалов. А теоретическую плотность распределения вероятности Р2(Q) представим в виде суммы двух экспоненциальных функций:
Р2(Q) = А1е−α1 (Q−Q1 )2 + А2е−α2 (Q−Q2 )2 |
(21) |
Значения параметров, входящих в функцию Р2(Q), также определяем с помощью экспериментального полигона распределения следующим образом:
1)величины Q1 и Q2 определим из условия равенства положения
максимумов мод экспериментального полигона и аппроксимирущей кривой. Первая мода имеет максимальное значение при Q = Q1 = 3,492, а вторая – при Q = Q2 = 4,90;
2) величины А1, А2, α1 и α2 определяем с помощью условий:
-при Q = 3,492 и Q = 4,908 значение Р2(Q) =(Рэкс(Q= 3,492)+ Рэкс(Q=4,908))/2 = 0,6625;
-площадь под кривой плотности распределения вероятности должна быть равна приблизительно единице, т.е. функция распределения вероятности, которая, как известно, является интегральной функцией, в
интервале от -∞ до +∞ должна быть равна (или близка к) единице. После расчетов получено, что А1 = А2 = 0,6625, а α1 = α2 = 5,5155 . С
помощью найденных параметров определены значения теоретической плотности распределения вероятности Р2(Q) для средних значений интервалов, которые записаны в табл. 8 и представлены в виде графиков на рис. 3. Для проверки в третьей строке табл. 8 приведены теоретические значения вероятности попадания отсчета в интервал Р2(Q)×∆N (как известно, для третьей гистограммы ∆N = 0,236). Суммируя полученные значения в третьей строке, можно проверить условие равенства единице площади под аппроксимирующей кривой.
Таблица 8
Средние |
2,548 |
2,784 |
3,02 |
3,256 |
3,492 |
3,728 |
3,964 |
4,2 |
4,436 |
4,672 |
4,908 |
5,144 |
5,38 |
5,616 |
5,852 |
интер- |
|||||||||||||||
значения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
валов Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рэкс(Q) |
0,0353 |
0,212 |
0,194 |
0,406 |
0,636 |
0,300 |
0,283 |
0,194 |
0,177 |
0,300 |
0,689 |
0,318 |
0,300 |
0,177 |
0,0177 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р2(Q) |
0,0048 |
0,0417 |
0,193885 |
0,4872 |
0,6625 |
0,4875 |
0,1987 |
0,0834 |
0,1987 |
0,4875 |
0,6625 |
0,4872 |
0,1938 |
0,0417 |
0,0048 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р2(Q)×∆N |
0,0011 |
0,0985 |
0,0458 |
0,115 |
0,1564 |
0,115 |
0,0458 |
0,0197 |
0,0458 |
0,115 |
0,1564 |
0,115 |
0,0458 |
0,0985 |
0,0011 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 Рэкс(Q)
Рэкс(Q) 
 Р2(Q)
Р2(Q)
|
0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вероятность |
0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
4 |
|
2 |
|
6 |
|
|
2 |
|
|
8 |
|
4 |
,2 |
|
|
6 |
|
|
2 |
|
|
8 |
|
4 |
|
8 |
|
|
6 |
|
2 |
||||
|
4 |
|
8 |
,0 |
|
5 |
|
9 |
|
2 |
6 |
4 |
|
|
3 |
|
7 |
|
0 |
4 |
,3 |
|
|
1 |
5 |
||||||||||||||
|
,5 |
|
|
,7 |
|
3 |
|
|
,2 |
|
,4 |
|
,7 |
|
,9 |
|
|
|
,4 |
|
,6 |
|
,9 |
|
,1 |
|
5 |
|
|
,6 |
|
,8 |
|
||||||
|
2 |
|
2 |
|
|
|
3 |
3 |
|
3 |
|
3 |
|
|
4 |
|
4 |
|
4 |
|
5 |
|
|
|
5 |
|
5 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Средние значения интервалов |
|
|
|
|
|
|
|
||||||||||||||||||||
Рис.3. Экспериментальный полигон распределения и аппроксимирующая функция плотности
(для гистограммы 3, вариант 1)
Из табл. 8 и рис. 3 следует, что отличие в некоторых точках теоретической зависимости от экспериментальной довольно значительное, при этом площадь под аппроксимирующей кривой равна 1,175, т.е. больше единицы. Поэтому рассмотрим еще один вариант аппроксимирующей функции:
Р21(Q) = А11е−α11 |
|
Q−Q1 |
|
+ А21е−α12 |
|
Q−Q2 |
|
|
|
|
|
|
(22) |
||||
|
|
|
|
|||||
Параметры функции Р21(Q) находим с помощью тех же условий, перечисленных выше. В результате расчетов получены следующие
результаты А11 = А21 = 0,6625, а α11 = α21 = 2,65. Расчет значений
экспериментального полигона распределения и теоретической плотности распределения вероятности представлены в табл. 9 и на рис. 4.
Из рис.4 видно, что последняя аппроксимирующая функция визуально имеет максимальное совпадение с полигоном распределения. При этом

|
|
|
|
|
|
|
|
|
|
|
Таблица 9 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Средние |
2,548 |
2,784 |
3,02 |
3,256 |
3,492 |
3,728 |
3,964 |
4,2 |
4,436 |
4,672 |
4,908 |
5,144 |
5,38 |
5,616 |
5,852 |
интерв- |
|||||||||||||||
значения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
алов Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рэкс(Q) |
0,0353 |
0,212 |
0,194 |
0,406 |
0,636 |
0,300 |
0,283 |
0,194 |
0,177 |
0,300 |
0,689 |
0,318 |
0,300 |
0,177 |
0,0177 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р2(Q) |
0,055 |
0,103 |
0,194 |
0,362 |
0,678 |
0,383 |
0,243 |
0,202 |
0,243 |
0,383 |
0,678 |
0,362 |
0,194 |
0,103 |
0,055 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р2(Q)×∆N |
0,01 |
0,02 |
0,04 |
0,08 |
0,16 |
0,09 |
0,05 |
0,04 |
0,05 |
0,09 |
0,16 |
0,08 |
0,04 |
0,02 |
0,01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
суммирование третьей строки в табл. 9 дает значение 1,0021, т.е. площадь под аппроксимирующей кривой близка к единице.

 Рэкс(Q)
Рэкс(Q) 
 Р2(Q)
Р2(Q)
|
0,8 |
|
|
|
|
|
|
|
|
0,7 |
|
|
|
|
|
|
|
Вероятность |
0,6 |
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
2,548 |
3,02 |
3,492 |
3,964 |
4,436 |
4,908 |
5,38 |
5,852 |
|
|
|
Средние значения интервалов |
|
||||
Рис. 4. Экспериментальный полигон распределения и аппроксимирующая функция плотности
(для гистограммы 3, вариант 2)
