χ 2 <χq2, т.е. гипотеза о законе распределения вероятности

подтверждается по критерию согласия Пирсона.

Таким образом, для дальнейшего анализа и представления результата измерения можно считать, что исходный массив наилучшим образом описывается двухмодальным законом распределения, плотность распределения вероятности которого определяется выражением:

где А11 = А21 = 0,6625, а α11 = α12 = 2,65.

2.7. ОПРЕДЕЛЕНИЕ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ

2.7.1.Общие сведения о характеристиках положения закона распределения вероятности и их оценках

Необходимо учитывать, что результатом многократного измерения

следует считать оценку некоторой характеристики положения закона распределения вероятности и доверительный интервал, в котором может находиться значение этой оценки с заданной вероятностью [5].

При этом, как показывает практика, основная часть материальных и временных ресурсов при измерениях тратится именно на определение характеристики положения, так как с характеристикой положения идентифицируется значение измеряемой величины. А при вероятностном описании неточности результата многократного измерения именно характеристика положения, являясь показателем качества измерения, определяет значение систематической составляющей неточности измерения.

Поэтому выбор эффективной оценки характеристики положения, в первую очередь, влечет за собой снижение затрат или повышение точности измерения, а неэффективная оценка характеристики положения может повлечь за собой завышенную оценку границ доверительного интервала, эксцесса, контрэксцесса, и т.п., т.е. всех последующих оценок, кроме энтропийных, которые определяются законом распределения. А из курса «Теоретической метрологии» известно, что наиболее эффективной оценкой является оценка, имеющая минимальное рассеивание из всех возможных несмещенных оценок. Большое внимание выбору наиболее эффективной оценки характеристики положения уделяют авторы в работе [2].

В качестве оценки характеристики положения в работе [2]

предлагаются среднее арифметическое, оценки медианы, центра размаха, центра сгибов. Далее указывается, что в симметричном распределении эти оценки совпадают, но их дисперсии разные и зависят от

закона распределения вероятности, которому подчиняется результат измерения.

Например, если для распределения Лапласа определить дисперсию рассеяния оценки характеристики положения в виде оценки медианы

центра медианой в два раза эффективнее, а следовательно, для достижения той же точности результата измерения требуется в два раза меньший объем выборки исходных данных. А для строго ограниченных распределений (равномерного, арксинусоидального, трапецеидального) высокой

эффективностью обладает оценка центра размахаQp . Так, при

Как правило, в качестве оценки центра распределения среднее арифметическое значение применяется для класса распределений, близких к нормальным.

Оценка медианы Qм определяется по формулам

Являясь 50% - ным квантилем оценка медианы делит общее количество отсчетов случайной величины пополам (количество отсчетов до оценки медианы и после должно быть одинаковое).

Как правило, оценка медианы является наиболее эффективной для симметричных экспоненциальных островершинных распределений. И это естественно, так как в островершинных распределениях отсчеты располагаются более плотно в месте экстремума плотности распределения вероятности. Рекомендуется применение оценки медианы и для несимметричных распределений, так как в этом случае доверительные интервалы в одну и другую сторону от центра распределения будут неодинаковые и для их расчета целесообразно поделить всю площадь, заключенную функцией плотности вероятности, пополам.

Оценка центра размаха Qр определяется в виде полусуммы крайних членов статистического ряда:

Центр размаха может применяться для ограниченных распределений, близких к равномерному, трапецеидальному, арксинусоидальному.

Оценка центра сгибов Qc чаще всего применяется для

двухмодальных симметричных распределений. Эта оценка определяется полусуммой координат 25% - ной и 75% - ной квантилей распределения:

Применение оценки центра сгибов в качестве оценки характеристики положения для двухмодальных симметричных распределений связано с тем, что наиболее плотно отсчеты располагаются в областях 25% - ной и 75% - ной квантилей, которые принято называть сгибами распределения.

Приведенные в данном пункте рекомендации по выбору оценки центра распределения не могут рассматриваться студентом как обязательные, так как эффективность той или иной оценки зависит от конкретных параметров закона распределения вероятности, в

частности от эксцесса. Так, например, если сравнить эффективность оценки медианы с эффективностью среднего арифметического для класса некоторых экспоненциальных распределений, то выяснится, что для островершинных распределений с контрэксцессом до значений κ ≈ 0,515 оценка характеристики положения в виде медианы эффективнее, а с

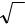
большими значениями контрэксцесса эффективнее оценка в виде среднего арифметического.

Иногда в условиях, когда нет еще данных о законе распределения вероятности, в качестве предварительной оценки характеристики положения может применяться округленное значение медианы всех четырех оценок:

Если при выполнении курсовой работы студент не сможет найти требуемых рекомендаций для выбора той или иной оценки характеристики положения ни в данном пособии, ни в справочной литературе, он применяет в качестве оценки характеристики положения закона распределения вероятности среднее арифметическое.

2.7.2. Определение оценки характеристики положения

Наиболее приемлемая оценка характеристики положения может быть определена двумя способами.

1. Первым способом оценка характеристики положения определяется по минимальному рассеиванию (минимальной дисперсии) оценки при данном количестве измерений. Для перечисленных выше оценок числовых характеристик, которые могут применяться в качестве оценок характеристик положения, рассеивание может быть определено по различным формулам [2].

Известно, что стандартное отклонение среднего арифметического при многократном измерении определяется по формуле

Дисперсию оценки медианы (50%-ная квантиль эмпирического распределения, т.е. Р = 0,5) можно определить с помощью формулы

[5]. В соответствии с этим методом составляется функция правдоподобия, которая зависит как от независимых случайных величин (значений вариационного ряда), так и от параметра Θ , которым может быть любой параметр, перечисленный в п. 9.

Если функция L дифференцируемая (очень важное свойство, например, трапецеидальное распределение не имеет производной в точках перегиба функции плотности распределения вероятности, аналогично и при равномерном распределении вероятности отсутствует производная при

Qi = Qmax и Qi = Qmin), то для нахождения оценки наибольшего правдоподобия необходимо решить уравнение

определить параметр Θ и сравнить его с параметрами, определенными по формулам, приведенным в п.9. Ближайший параметр к найденному значению Θ должен быть принят в качестве оценки центра распределения.

Ценность применения метода наибольшего правдоподобия (метода Фишера) состоит в том, что с его помощью может быть проведен анализ любой представленной в виде аналитического выражения дифференцируемой функции, характеризующей плотность распределения вероятности.

ПРИМЕР. Теоретическая функция плотности распределения вероятности, как следует из предыдущего пункта, описывается выражением

1 А1е−α1 Q−Q + А1е−α1 Q−Q

Р2 (Q) = 1 1 1 2 2 2 ,

где А11 = А21 = 0,6625, Q1 = 3,492, Q2 = 4,908, α11 = α12 = 2,65.

Для анализируемого массива оценки числовых характеристик, определенные по формулам (38) – (42), имеют следующие значения:

среднее арифметическое Q = 4,193333;

стандартное отклонение SQ = 0,842812;

оценка медианы равна Q м = 4,2;

оценка левого сгиба (25% квантиль) при Q лев = 3,492, а оценка правого

сгиба (75% квантиль) – Q пр = 4,908, соответственно оценка центра

сгибов Qс = (4,908+3,492)/2 = 4,2;

оценка контрэксцесса к= 0,76917.

Для сравнения проведем анализ эффективности использования трех оценок числовых характеристик: среднего арифметического, медианы и центра сгибов. Одновременно учитываем, что приведенное в примере распределение плотности вероятности двухмодальное, а для такого