
- •Раздел 1. Алгебра и геометрия Лекция 2. Тема 1.3. Логика, множества, функции
- •1. Основные элементарные функции
- •1.1. Числовые функции и способы их задания. Классификация элементарных функций
- •1. Примеры числовых множеств
- •2. Свойства множества действительных чисел
- •1.2. Функции заданные явно и неявно и параметрически
- •2. Графики элементарных функций
- •2.1. Степенная функция
- •2.2. Показательная функция
- •2.3. Логарифмическая функция
- •2.4. Тригонометрические функции
- •2.5. Обратные тригонометрические функции
2.5. Обратные тригонометрические функции
2.5.1. Функция
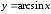
Величина
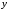 называется углом. Величина
называется углом. Величина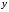 определяется равенством
определяется равенством
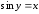 . (1)
. (1)
Поскольку функция
синуса является периодической, то
соотношению (1) удовлетворяет множество
значений
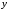 .
Среди всевозможных значений функции
(1) выбирают только те, которые попадают
в интервал
.
Среди всевозможных значений функции
(1) выбирают только те, которые попадают
в интервал
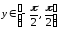 .
.
Последний и
составляет область изменения функции
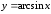 (
(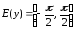 ).
Поскольку значение функции (1) по модулю
не превосходит единице, то областью
определения функции
).
Поскольку значение функции (1) по модулю
не превосходит единице, то областью
определения функции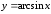 является
является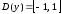 .
.
График этой функции представлен на рис. 1.
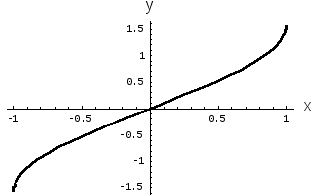
Рис. 1. Функция
арксинуса
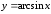 .
.
2.5.2. Функция
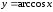
Величина
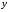 называется углом. Величина
называется углом. Величина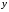 определяется равенством
определяется равенством
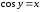 . (1)
. (1)
Поскольку функция
косинуса является периодической, то
соотношению (1) удовлетворяет множество
значений
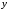 .
Среди всевозможных значений функции
(1) выбирают только те, которые попадают
в интервал
.
Среди всевозможных значений функции
(1) выбирают только те, которые попадают
в интервал
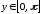 .
.
Последний и
составляет область изменения функции
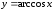 (
(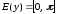 ).
Поскольку значение функции (1) по модулю
не превосходит единице, то областью
определения функции
).
Поскольку значение функции (1) по модулю
не превосходит единице, то областью
определения функции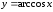 является
является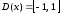 .
.
График этой функции представлен на рис. 1.
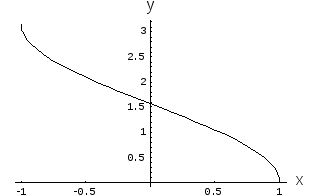
Рис. 1. Функция
арккосинуса
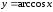 .
.
2.5.3. Функция
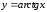
Величина
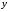 называется углом. Величина
называется углом. Величина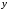 определяется равенством
определяется равенством
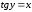 . (1)
. (1)
Поскольку функция
тангенса является периодической, то
соотношению (1) удовлетворяет множество
значений
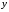 .
Среди всевозможных значений функции
(1) выбирают только те, которые попадают
в интервал
.
Среди всевозможных значений функции
(1) выбирают только те, которые попадают
в интервал
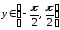 .
.
Последний и
составляет область изменения функции
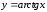 (
(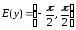 ).
Поскольку функция (1) может принимать
любое действительное значение, то
областью определения функции
).
Поскольку функция (1) может принимать
любое действительное значение, то
областью определения функции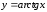 является
является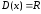 .
.
График этой функции представлен на рис. 1.
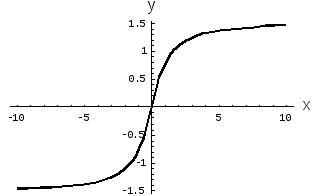
Рис. 1. Функция
арктангенса
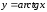 .
.
2.5.4. Функция
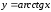
Величина
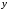 называется углом. Величина
называется углом. Величина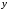 определяется равенством
определяется равенством
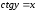 . (1)
. (1)
Поскольку функция
котангенса является периодической, то
соотношению (1) удовлетворяет множество
значений
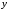 .
Среди всевозможных значений функции
(1) выбирают только те, которые попадают
в интервал
.
Среди всевозможных значений функции
(1) выбирают только те, которые попадают
в интервал
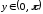 .
.
Последний и
составляет область изменения функции
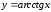 (
(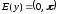 ).
Поскольку функция (1) может принимать
любое действительное значение, то
областью определения функции
).
Поскольку функция (1) может принимать
любое действительное значение, то
областью определения функции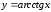 является
является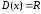 .
.
График этой функции представлен на рис. 1.
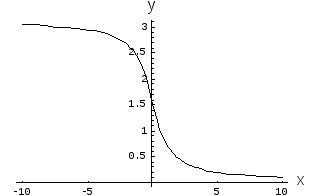
Рис. 1. Функция
арккотангенса
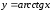 .
.
1В учебнике Шнейдера В. Е. и др. «Краткий курс высшей математики. Т. 1» к основным элементарным функциям относят постоянную.
2В учебнике Шнейдера В. Е. и др. «Краткий курс высшей математики. Т. 1» добавлено «не равное нулю».
