
- •Раздел 1. Алгебра и геометрия Лекция 2. Тема 1.3. Логика, множества, функции
- •1. Основные элементарные функции
- •1.1. Числовые функции и способы их задания. Классификация элементарных функций
- •1. Примеры числовых множеств
- •2. Свойства множества действительных чисел
- •1.2. Функции заданные явно и неявно и параметрически
- •2. Графики элементарных функций
- •2.1. Степенная функция
- •2.2. Показательная функция
- •2.3. Логарифмическая функция
- •2.4. Тригонометрические функции
- •2.5. Обратные тригонометрические функции
2.2. Показательная функция
Показательная функция задается следующим аналитическим выражением:
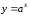 , (1)
, (1)
где
 и
и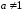 - действительное число.
- действительное число.
Показательная
функция с указанными ограничениями для
основания степени
 определена для любых значений
определена для любых значений (
( ).
Вид показательной функции существенно
зависит от основания степени
).
Вид показательной функции существенно
зависит от основания степени .
Если
.
Если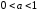 ,
то функция является убывающей (см. рис.
1). Если
,
то функция является убывающей (см. рис.
1). Если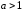 ,
то функция является возрастающей (см.
рис. 2).
,
то функция является возрастающей (см.
рис. 2).
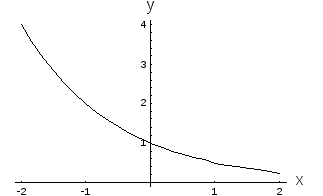
Рис. 1. Показательная
функция
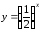 .
.
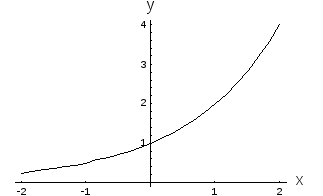
Рис. 2. Показательная
функция
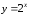 .
.
Отметим, что графики
всех показательных функций проходят
через одну и ту же точку с координатами
 .
.
2.3. Логарифмическая функция
Логарифмическая функция задается следующим аналитическим выражением:
 , (1)
, (1)
где
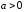 и
и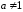 - действительное число. Она понимается
как число, которое должно быть степенью
числа
- действительное число. Она понимается
как число, которое должно быть степенью
числа ,
чтобы получить
,
чтобы получить .
Иначе говоря, значение функции должно
быть таким, чтобы выполнялось соотношение
.
Иначе говоря, значение функции должно
быть таким, чтобы выполнялось соотношение
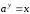 .
.
Число
 называется основанием логарифмической
функции. Поскольку любая степень
положительного числа дает также
положительное число, то областью
определения логарифмической функции
(1) является множество положительных
вещественных чисел (
называется основанием логарифмической
функции. Поскольку любая степень
положительного числа дает также
положительное число, то областью
определения логарифмической функции
(1) является множество положительных
вещественных чисел (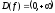 ).
Вид логарифмической функции существенно
зависит от величины основания логарифма
).
Вид логарифмической функции существенно
зависит от величины основания логарифма .
Если
.
Если ,
то функция является убывающей (см. рис.
1). Если
,
то функция является убывающей (см. рис.
1). Если ,
то функция является возрастающей (см.
рис. 2).
,
то функция является возрастающей (см.
рис. 2).
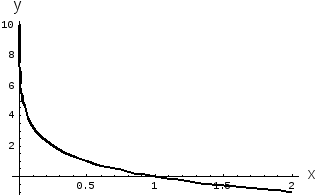
Рис. 1. Логарифмическая
функция
 .
.
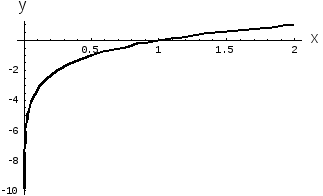
Рис. 2. Логарифмическая
функция
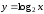 .
.
Отметим, что графики
всех логарифмических функций проходят
через одну и ту же точку с координатами
 .
.
2.4. Тригонометрические функции
2.4.1. Функция
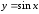
Аргумент
 называется углом. Угол определяется
как отношение длины дуги части окружности,
проведенной из вершины угла как из
центра, к величине радиуса окружности.
Угол является безразмерной величиной.
Однако условно его считают выраженным
в радианах. Отметим, что угол может
выражаться в градусах. Для острых углов,
т. е. для углов величиной
называется углом. Угол определяется
как отношение длины дуги части окружности,
проведенной из вершины угла как из
центра, к величине радиуса окружности.
Угол является безразмерной величиной.
Однако условно его считают выраженным
в радианах. Отметим, что угол может
выражаться в градусах. Для острых углов,
т. е. для углов величиной функция синуса определяется как отношение
противолежащего катета к гипотенузе
прямоугольного треугольника. Для
остальных значений аргумента функция
синуса определяется как ордината конца
подвижного радиуса единичной окружности.
Очевидно, что функция
функция синуса определяется как отношение
противолежащего катета к гипотенузе
прямоугольного треугольника. Для
остальных значений аргумента функция
синуса определяется как ордината конца
подвижного радиуса единичной окружности.
Очевидно, что функция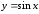 имеет период, равный
имеет период, равный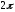 .
График этой функции представлен на рис.
1.
.
График этой функции представлен на рис.
1.

Рис. 1. Функция
синуса
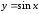 .
.
Областью определения
функции синуса является все множество
действительных чисел (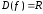 ).
).
2.4.2. Функция
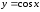
Для острых углов,
т. е. для углов величиной
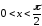 функция косинуса определяется как
отношение прилежащего катета к гипотенузе
прямоугольного треугольника. Для
остальных значений аргумента функция
косинуса определяется как абсцисса
конца подвижного радиуса единичной
окружности. Очевидно, что функция
функция косинуса определяется как
отношение прилежащего катета к гипотенузе
прямоугольного треугольника. Для
остальных значений аргумента функция
косинуса определяется как абсцисса
конца подвижного радиуса единичной
окружности. Очевидно, что функция имеет период, равный
имеет период, равный .
График этой функции представлен на рис.
1.
.
График этой функции представлен на рис.
1.
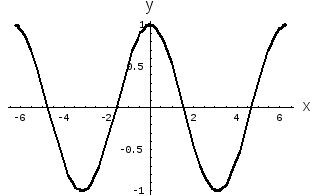
Рис. 1. Функция
косинуса
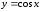 .
.
Областью определения
функции косинуса является все множество
действительных чисел (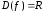 ).
).
2.4.3. Функция

Для острых углов,
т. е. для углов величиной
 функция тангенса определяется как
отношение противолежащего катета к
прилежащему прямоугольного треугольника
или как отношение синуса к косинусу
функция тангенса определяется как
отношение противолежащего катета к
прилежащему прямоугольного треугольника
или как отношение синуса к косинусу
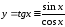 . (1)
. (1)
Для остальных
значений аргумента функция тангенса
определяется как отношение ординаты
конца подвижного радиуса единичной
окружности к его абсциссе или как
ордината точки пересечения подвижного
луча с прямой перпендикулярной оси
абсцисс и проходящей через точку с
координатами
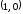 .
Функция
.
Функция имеет период, равный
имеет период, равный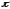 .
График этой функции представлен на рис.
1.
.
График этой функции представлен на рис.
1.

Рис. 1. Функция
тангенса
 .
.
Областью определения функции косинуса является все множество действительных чисел кроме тех, в которых функция косинуса обращается в нуль, т. е. кроме
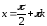 ,
,
где

 (
(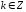 ).
).
2.4.4. Функция
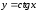
Для острых углов,
т. е. для углов величиной
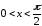 функция котангенса определяется как
отношение прилежащему катета
противолежащего к прямоугольного
треугольника или как отношение косинуса
к синусу
функция котангенса определяется как
отношение прилежащему катета
противолежащего к прямоугольного
треугольника или как отношение косинуса
к синусу
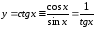 . (1)
. (1)
Для остальных
значений аргумента функция тангенса
определяется как отношение абсциссы
конца подвижного радиуса единичной
окружности к его ординате или как
абсцисса точки пересечения подвижного
луча с прямой перпендикулярной оси
ординат и проходящей через точку с
координатами
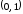 .
Функция
.
Функция имеет период, равный
имеет период, равный .
График этой функции представлен на рис.
1.
.
График этой функции представлен на рис.
1.
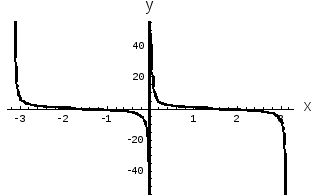
Рис. 1. Функция
тангенса
 .
.
Областью определения функции котангенса является все множество действительных чисел кроме тех, в которых функция синуса обращается в нуль, т. е. кроме
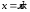 ,
,
где

 (
(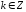 ).
).
