- •Раздел 1. Алгебра и геометрия Лекция 2. Тема 1.3. Логика, множества, функции
- •1. Основные элементарные функции
- •1.1. Числовые функции и способы их задания. Классификация элементарных функций
- •1. Примеры числовых множеств
- •2. Свойства множества действительных чисел
- •1.2. Функции заданные явно и неявно и параметрически
- •2. Графики элементарных функций
- •2.1. Степенная функция
- •2.2. Показательная функция
- •2.3. Логарифмическая функция
- •2.4. Тригонометрические функции
- •2.5. Обратные тригонометрические функции
Раздел 1. Алгебра и геометрия Лекция 2. Тема 1.3. Логика, множества, функции
1. Основные элементарные функции
1.1. Числовые функции и способы их задания. Классификация элементарных функций
Если одно числовое
множество
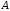 отражается в другое числовое
множество
отражается в другое числовое
множество
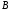 ,
то говорят,
что задана числовая функция. Функции
задаются либо аналитически, либо
графически либо таблично.
,
то говорят,
что задана числовая функция. Функции
задаются либо аналитически, либо
графически либо таблично.
К основным1элементарнымфункциямотносят следующие:
степенную функцию;
показательную;
логарифмическую;
тригонометрические;
обратные тригонометрические.
Элементарныефункцииполучаются из основных элементарных функций с использованием конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции. Количество этих операций не должно зависеть от аргумента.
К алгебраическимфункциямотносят следующие:
целую рациональную функцию или многочлен;
дробную рациональную;
иррациональную функцию, т.е. ту, в которой аргумент или выражение ее содержащее, возводится в нецелую степень.
К трансцендентнымфункциямотносят все неалгебраические функции.
Замечания.
1. Примеры числовых множеств
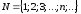 - множество
натуральных чисел.
- множество
натуральных чисел.
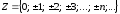 - множество целых
чисел.
- множество целых
чисел.
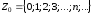 - множество целых
неотрицательных чисел.
- множество целых
неотрицательных чисел.
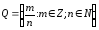 - множество
рациональных чисел.
- множество
рациональных чисел.
 - множество
действительных чисел.
- множество
действительных чисел.
2. Свойства множества действительных чисел
Множество
 действительных чисел обладает следующими
свойствами.
действительных чисел обладает следующими
свойствами.
1. Оно упорядоченное:
для двух любых различных чисел
 и
и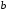 имеет место одно из двух соотношений
имеет место одно из двух соотношений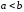 либо
либо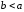 .
.
2. Множество
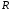 плотное: между любыми двумя различными
числами
плотное: между любыми двумя различными
числами и
и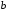 (
(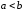 )
содержится бесконечное множество
действительных чисел
)
содержится бесконечное множество
действительных чисел ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
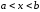 .
.
3. Множество
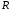 непрерывное.
непрерывное.
Пусть множество
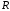 разбито на два непустых подмножества
разбито на два непустых подмножества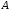 и
и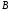 таких, что каждое действительное число
содержится только в одном классе и для
каждой пары чисел
таких, что каждое действительное число
содержится только в одном классе и для
каждой пары чисел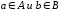 выполняется неравенство
выполняется неравенство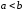 .
.
Тогда (свойство
непрерывности) существует единственное
число
 ,
удовлетворяющее неравенству
,
удовлетворяющее неравенству
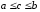 (
(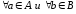 ).
).
Оно отделяет числа
из классов
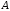 и
и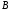 .
Число
.
Число является либо наибольшим числом в классе
является либо наибольшим числом в классе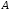 (тогда в классе
(тогда в классе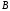
 нет наименьшего числа) либо наименьшим
числом в классе
нет наименьшего числа) либо наименьшим
числом в классе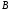 (тогда в классе
(тогда в классе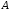
 нет наибольшего числа).
нет наибольшего числа).
1.2. Функции заданные явно и неявно и параметрически
Функция называется
явнозаданной, если
действия, выполняемые для ее вычисления,
указаны и можно их осуществить для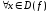 .
.
Функция может быть задана неявно. Форма ее задания в имеет вид
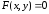 , (1)
, (1)
где
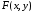 - символ функции двух аргументов, заданной
явно.
- символ функции двух аргументов, заданной
явно.
Например,
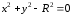 .
.
Теперь нет явного
правила вычисления функции
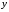 по ее аргументу
по ее аргументу .
Однако, в этом случае оно может быть
легко получено в виде
.
Однако, в этом случае оно может быть
легко получено в виде
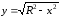 или
или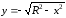 .
.
Под неявно заданной функцией
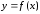
понимается такая, подстановка которой в уравнение (1) обращает его в тождество
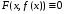 .
.
Зависимость
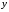 от
от можно задать с помощью третьей переменной
можно задать с помощью третьей переменной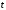 в виде
в виде
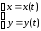 ,
,
где
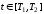 .
.
Этот способ задания
функции называется параметрическим.
В частности при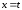 получается
получается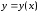 - явный способ задания функции.
- явный способ задания функции.
2. Графики элементарных функций
2.1. Степенная функция
Степеннаяфункциязадается следующим аналитическим выражением:
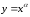 , (1)
, (1)
где
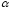 - действительное число2.
- действительное число2.
Область определения
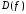 степенной функции зависит от значения
показателя степени
степенной функции зависит от значения
показателя степени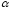 .
Например, если
.
Например, если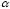 - целое положительное (натуральное)
число, то областью определения степенной
функции является множество действительных
чисел
- целое положительное (натуральное)
число, то областью определения степенной
функции является множество действительных
чисел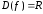 .
В этом случае получается следующий ряд
степенных функций:
.
В этом случае получается следующий ряд
степенных функций: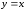 ,
,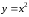 ,
,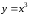 …
Степенные функции с нечетными показателями
степени являются нечетными, а с четными
показателями степени – четными. Графики
некоторых нечетных функций приведены
на рис. 1, а четных – на рис. 2.
…
Степенные функции с нечетными показателями
степени являются нечетными, а с четными
показателями степени – четными. Графики
некоторых нечетных функций приведены
на рис. 1, а четных – на рис. 2.
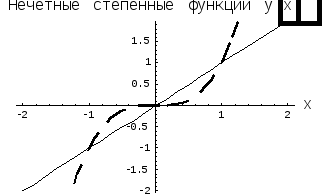
Рис. 1.
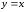 - сплошная линия,
- сплошная линия,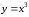 - пунктирная линия
- пунктирная линия
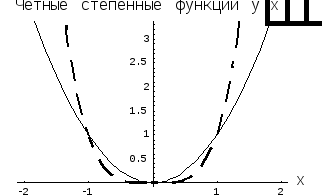
Рис. 2.
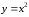 - сплошная линия,
- сплошная линия,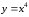 - пунктирная линия
- пунктирная линия
Если
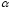 - целое отрицательное число, то в этом
случае степенная функция определена
для всех действительных значений
- целое отрицательное число, то в этом
случае степенная функция определена
для всех действительных значений ,
кроме
,
кроме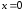 .
Если степень
.
Если степень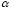 является четным отрицательным числом,
то степенная функция является четной.
В противном случае она является нечетной.
Эти утверждения проиллюстрированы на
рис. 3 и 4.
является четным отрицательным числом,
то степенная функция является четной.
В противном случае она является нечетной.
Эти утверждения проиллюстрированы на
рис. 3 и 4.
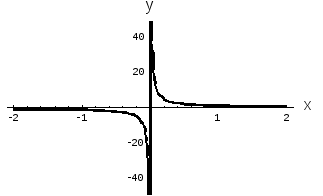
Рис. 3. Степенная
функция
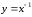
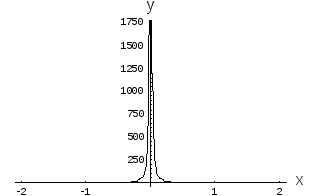
Рис. 4. Степенная
функция
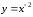
Среди степенных
функций с показателем степени, являющимся
рациональной дробью рассмотрим функцию
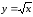 .
Поскольку рассматривается арифметическое
значение корня, то областью определения
функции будет множество неотрицательных
действительных чисел (
.
Поскольку рассматривается арифметическое
значение корня, то областью определения
функции будет множество неотрицательных
действительных чисел (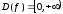 ).
График этой степенной функции представлен
на рис. 5.
).
График этой степенной функции представлен
на рис. 5.
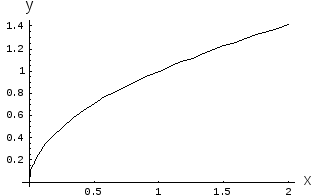
Рис. 5. Степенная
функция
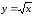
График функции
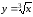 представлен на рис. 6. Областью определения
функции является вся действительная
ось.
представлен на рис. 6. Областью определения
функции является вся действительная
ось.
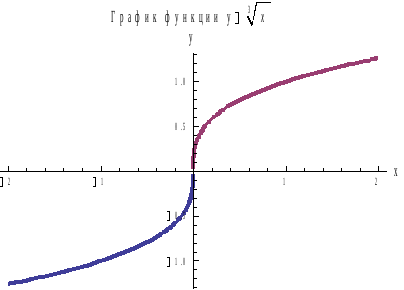
Рис. 6. Степенная
функция