
MODELIROVANIE_metodichka
.pdf
Другими словами, систему (5) решают n раз, каждый раз при новом значении Bii. В результате решения находят:
m 11 ,m 12 , ... ,m1n , |
|
|
m 21 ,m 2 , ... ,m 2n , |
(6) |
|
, |
||
|
||
m n 1 ,m n 2 , ... ,mnn . |
|
Следует отметить, что решение системы уравнений (5) мо- жет быть получено только с точностью до числового множителя.
Далее вычисляют величины:
Mij = |
|
mij |
|
, |
(7) |
|
|
|
|
||||
n |
||||||
|
|
|
|
|
||
|
|
åmij2 |
|
|
|
|
|
|
j =1 |
|
|
|
где i, j = 1, 2, . . ., n.
Очевидно, при каждом значении i = 1, 2, . . ., n выполняется условие нормировки:
|
|
n |
|
|
|
|
åMij2 = 1 . |
(88) |
|
|
|
j=1 |
|
|
Искомая зависимость между переменными имеет вид |
|
|||
Z1 = M11 (X1 − X1s )+ ...+ M1n (X n − X ns ), |
|
|||
Z2 |
= M 21(X1 |
− X1s )+ ...+ M 2n (X n − X ns ), |
(9) |
|
.............................................................. |
||||
|
||||
Zn |
= M n1(X1 |
− X1s )+ ...+ M nn (X n − X ns ). |
|
|
При числе факторов n > 2 приведение уравнения к канони- ческому виду требует значительного объема вычислений, поэто- му его следует осуществлять с помощью ЭВМ.
110
Угол поворота ϕ новых координатных осей относительно
старых определяют по формуле
tg 2ϕ = |
|
b12 |
|
. |
(10) |
b |
− b |
22 |
|||
11 |
|
|
|
||
Для двух факторов соотношение между переменными X1 , X2 и Z1 , Z2 в ряде случаев, целесообразно, представить в виде:
Х1 = (Z1 + X1s )cosϕ − (Z2 + X2s X2 = (Z1 + X1s )sinϕ + (Z2 + X2s
)sinϕ ; |
(11) |
)cosϕ . |
(12) |
|
y |
|
|
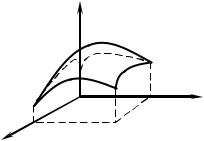
Геометрический образ, |
|
|
|
соответствующий |
функции |
||
|
|
|
|||
|
|
|
отклика y, называют поверх- |
||
|
|
|
ностью отклика (рис. 1). Ко- |
||
|
|
|
ординатное пространство, по |
||
|
|
|
осям которого отложены фак- |
||
|
|
х2 |
торы, |
называют факторным |
|
х1 |
|||||
|
|
|
пространством. |
|
|
|
|
|
|
||
Рис. 1. Поверхность отклика |
|
|
Для удобства |
рассмот- |
|
|
рения |
поверхность |
отклика |
||
|
|
|
|||
может быть представлена на факторной плоскости (x1, x2) линиями постоянных значений функции отклика (рис. 2).
На рис. 2, а поверхность отклика имеет вид «вершины» и соответствует области значений факторов, где расположен мак- симум величины у. Очевидно, аналогичный вид имеют линии по- стоянного уровня и в случае минимума функции у.
Поверхность, изображенная на рис. 2, б, характеризует плавное возрастание функции отклика с уменьшением фактора x1 и увеличением x2. Такую поверхность принято называть «стацио- нарным возвышением».
111
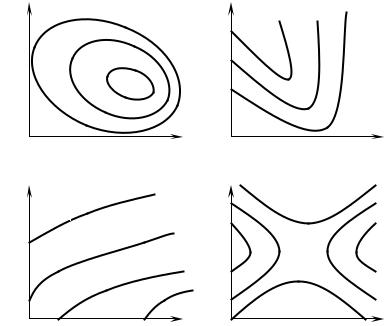
«Хребтом» называется поверхность, показанная на рис. 2, в. Его вершина соответствует наибольшим значениям функции от- клика. Аналогично располагаются линии постоянных значений у и в случае «оврага», дно которого соответствует минимальным значениям функции отклика.
Наконец, на рис. .2, г изображена поверхность, называемая «седлом». На двух ее участках наблюдается возрастание функции отклика, а на двух других – убывание.
Следует отметить, что на практике встречаются поверхно- сти отклика и с более сложной конфигурацией.
х2 |
х2 |
|
|
|
80 |
|
80 |
|
|
90 |
|
|
|
|
|
|
|
|
|
100 |
|
|
90 |
|
|
|
|
|
|
|
|
|
100 |
|
х1 |
|
|
|
х1 |
а |
|
|
б |
|
х2 |
х2 |
|
|
|
90 |
|
|
10 |
|
100 |
8 |
9 |
9 |
8 |
90 |
|
|
|
|
80 |
|
|
10 |
|
|
|
|
|
|
х1 |
|
|
|
х1 |
в |
|
|
г |
|
Рис. 2. Типы поверхностей отклика
112
Если число факторов больше двух, то для изображения по- верхности отклика пользуются ее двумерными сечениями. С этой целью каждый раз фиксируют все факторы, кроме двух.
Все многообразие поверхностей отклика, описываемых уравнением вида (1), можно разделить на три класса.
Кпервому – относят поверхности, имеющие экстремум (рис. 2, а). В этом случае все коэффициенты канонической формы (1) имеют одинаковые знаки, а центр поверхности находится вблизи центра эксперимента. Анализ таких поверхностей заканчивается после приведения уравнения регрессии к канонической форме.
Исследователю необходимо только поставить несколько опытов вблизи центра поверхности и убедиться, что значения функции отклика, предсказанные уравнением регрессии, достаточно хо- рошо совпадают с экспериментальными данными.
Во второй – входят поверхности типа «стационарного воз- вышения» (рис. 2, б). В этом случае некоторые коэффициенты канонической формы близки к нулю.
Ктретьему – относят поверхности типа «седло» (рис. 2, г). Они характеризуются тем, что коэффициенты канонической фор- мы имеют разные знаки, а центр поверхности находится поблизо- сти от центра опыта.
Имея дело с поверхностями отклика типа «стационарное возвышение» или «седло», исследователь должен пользоваться методами вычислительной математики и средствами вычисли-
тельной техники для нахождения условного экстремума критерия оптимальности с учетом ограничений, наложенных на влияющие факторы и остальные функции отклика.
Пример 1
Для построения математической модели, отражающей за- висимость эффективной вязкости помадной массы y (Па×с) от температуры x1 (°С) и массовой доли влаги x2 (%) при значении градиента скорости γ& = 5 с-1, было использовано ЦКРП, характе- ристики которого представлены в табл. 1.
113
Эксперименты проводили согласно матрице планирования с применением рандомизации. Каждый опыт дублировали два раза. В табл. 2 даны средние значения функции отклика по ре- зультатам двух параллельных опытов.
|
|
|
Характеристики планирования |
|
Таблица .1 |
||||
|
|
|
|
|
|||||
|
|
Параметр |
|
|
x1, °С |
|
x2, % |
||
|
Основной уровень |
|
|
|
30,0 |
|
|
10,0 |
|
|
Верхний уровень |
|
|
|
35,0 |
|
|
12,0 |
|
|
Нижний уровень |
|
|
|
25,0 |
|
|
8,0 |
|
|
Верхняя «звездная» точка |
|
|
37,05 |
|
|
12,82 |
||
|
Нижняя «звездная» точка |
|
|
22,95 |
|
|
7,18 |
||
|
Интервал варьирования |
|
|
5,0 |
|
|
2,0 |
||
|
|
|
|
Матрица ЦКРП |
|
Таблица 2 |
|||
|
|
|
|
|
|
||||
|
№ опыта |
|
X1 |
|
|
X2 |
|
Функция отклика |
|
|
|
|
|
|
|
y , Па×с |
|||
|
1 |
|
-1 |
|
-1 |
|
718,21 |
||
|
2 |
|
+1 |
|
-1 |
|
412,74 |
||
|
3 |
|
-1 |
|
+1 |
|
639,01 |
||
|
4 |
|
+1 |
|
+1 |
|
370,91 |
||
|
5 |
|
-a |
|
0 |
|
773,01 |
||
|
6 |
|
+a |
|
0 |
|
366,14 |
||
|
7 |
|
0 |
|
|
-a |
|
540,55 |
|
|
8 |
|
0 |
|
|
+a |
|
455,43 |
|
|
9 |
|
0 |
|
0 |
|
475,78 |
||
|
10 |
|
0 |
|
0 |
|
474,00 |
||
|
11 |
|
0 |
|
0 |
|
475,09 |
||
|
12 |
|
0 |
|
0 |
|
476,14 |
||
|
13 |
|
0 |
|
0 |
|
476,43 |
||
Обработку результатов ЦКРП проводили по типовой мето- дике. При этом были рассчитаны коэффициенты уравнения рег- рессии, определена значимость каждого из них. Установлено, что в соответствии с критерием Стьюдента, все коэффициенты явля- ются значимыми. Адекватность полученного уравнения регрес- сии устанавливали по критерию Фишера. Сравнение расчетного значения критерия Фишера с табличным показало, что уравнение регрессии адекватно описывает поверхность отклика.
114

Полученное уравнение регрессии в кодированных пере- менных выглядит следующим образом:
y = 475,25 -144,03X1 - 30,19X 2 + 9,25X1 X 2 + 47,62X12 +11,41X 22 .
Уравнение регрессии позволяет не только предсказать зна- чения функции отклика (эффективной вязкости) для заданных условий проведения эксперимента, но и дает информацию о фор- ме поверхности отклика. Исследование этой поверхности необ- ходимо для выбора оптимальных значений температуры и влаж- ности помадной массы.
Приведем уравнение регрессии к каноническому виду. Дифференцируя его по X1 и X 2 , составим систему алгебраиче-
ских уравнений по форме (2): |
|
||||
ì |
¶Y |
|
= -144,03 + 9,25X 2 + 95,24X1 |
= 0; |
|
ï |
|
|
|||
¶X1 |
|||||
ï |
|
|
|
||
í |
¶Y |
|
|
||
ï |
= -30,19 + 9,25X1 + 22,82X 2 = 0. |
||||
|
|||||
ï |
¶X2 |
|
|
|
|
î |
|
|
|
||
Решая эту систему относительно X1 и X 2 , вычислим ко- |
|||||
ординаты центра поверхности: X1s = 1,44 и X 2s |
= 0,73. |
||||
Подставляя найденные значения в исходное уравнение, рассчи- таем значение функции отклика в центре поверхности Ys = 360,36 .
Составим характеристические уравнения в виде (3):
47,62 - B 0,5 × 9,25 = 0 , 0,5 × 9,25 11,41 - B
решая которое, находим его корни B11 = 48,2 и B22 = 10,83 . Уравнение регрессии в канонической форме примет вид:
Y = 360,36 + 48,21Z12 +10,83Z22 .
115
Как видно из этого уравнения, коэффициенты канониче- ской формы имеют положительные одинаковые знаки. Это дает основание предполагать, что исследуемая поверхность является экстремальной и имеет вид «впадины».
Перейдем к нахождению соотношений между координата- ми X1 , X 2 и Z1 , Z2 . Составим для этого систему уравнений: по форме (5)
ì (47,62 - 48,21)m11 + 0,5 × 9,25 × m12 = 0, íî0,5 × 9,25 × 9,25m11 + (11,41 -10,83)m12 = 0,
решая которое относительно m11 и m12 , получим m11 = 7,96 × m12 .
Решение данной системы уравнений возможно только с точностью до числового множителя, поэтому, полагая m12 = 1,
определяем m11 |
= 7,96. |
|
|
|
|
|
|
|
|
|
|
||||
В соответствии с формулой (7), вычисляем величины: |
|||||||||||||||
M11 = |
|
|
|
|
7,96 |
= 0,99 ; |
M12 = |
|
|
|
|
1 |
= 0,12 . |
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
7,962 +1 |
||||||||||||
7,962 + 1 |
|
|
|
|
|
||||||||||
Составим вторую систему уравнений: |
|
|
|
|
|
|
|
||||||||
|
|
|
|
(47,62 -10,83)m21 + 0,5 × 9,25 × m22 = 0, |
|
|
|||||||||
|
|
|
|
0,5 × 9,25 × m21 + (11,41 -10,83)m22 = 0, |
|
|
|
|
|||||||
решая которое относительно m21 |
и m22 , получим m21 = 0,12 × m22 . |
||||||||||||||
Примем m22 = 1, находимm21 = 0,12. |
|
|
|
|
|
|
|
||||||||
По формуле (7) определяем величины: |
|
|
|
|
|
|
|
||||||||
M21 = |
|
|
|
0,12 |
= 0,12 ; |
M22 |
= |
|
1 |
|
= 1. |
||||
|
|
|
|
|
|
|
|||||||||
|
|
0,122 +1 |
|||||||||||||
0,122 +1 |
|
|
|
|
|
|
|
||||||||
116
Представим связь между координатами в виде (9)
Z1 = 0,99(X1 -1,44)+ 0,12(X 2 - 0,73),
Z2 = 0,12(X1 -1,44)+ (X2 - 0,73)
или после преобразований
Z1 = 0,99X1 + 0,12X 2 -1,5 ,
Z2 = 0,12X1 + X 2 - 0,9 .
Угол поворота j новых координатных осей относительно старых в соответствии с формулой (10) равен ϕ = 7,01 . Он поло-
жительный, следовательно, новые координатные оси при канони-
ческом преобразовании повернуты относительно старых против часовой стрелки.
Пример 2
Для изучения адгезионных и реологических свойств теста было применено центральное композиционное ротатабельное планирование. В качестве функций отклика были использованы следующие показатели: адгезионная прочность теста y1 (Н) и эф- фективная вязкость теста y2 (Па×с); в качестве факторов, влияю- щих на реологические свойства, были выбраны – массовая доля ПАВ x1 (%) и pH используемой для замеса теста воды x2 (ед. pH). Пределы их изменения представлены в табл. 3.
Характеристики планирования |
Таблица 3 |
|
|
||
Параметр |
x1, % |
x2, ед.рН |
Основной уровень |
0,75 |
9,50 |
Верхний уровень |
0,45 |
1,50 |
Нижний уровень |
1,20 |
11,0 |
Верхняя «звездная» точка |
0,30 |
8,0 |
Нижняя «звездная» точка |
0,015 |
7,25 |
Интервал варьирования |
1,425 |
11,75 |
117

Эксперименты проводили согласно матрице планирования с использованием рандомизации, каждый опыт дублировали два раза. В табл. 4 представлены средние арифметические значения функций отклика y1 и y2, полученных по результатам двух парал- лельных опытов.
|
|
Матрица ЦКРП |
Таблица 4 |
|
|
|
|
||
№ опыта |
X1 |
X2 |
y1 |
y2 |
1 |
-1 |
-1 |
8,46 |
5,17×103 |
2 |
+1 |
-1 |
9,21 |
4,88×103 |
3 |
-1 |
+1 |
6,48 |
4,87×103 |
4 |
+1 |
+1 |
8,68 |
4,58×103 |
5 |
-1,41 |
0 |
8,95 |
3,14×103 |
6 |
+1,41 |
0 |
7,22 |
5,02×103 |
7 |
0 |
-1,41 |
7,85 |
4,67×103 |
8 |
0 |
+1,41 |
9,25 |
5,44×103 |
9 |
0 |
0 |
7,77 |
4,87×103 |
10 |
0 |
0 |
7,80 |
4,86×103 |
11 |
0 |
0 |
7,80 |
4,86×103 |
12 |
0 |
0 |
7,77 |
4,87×103 |
13 |
0 |
0 |
7,77 |
4,87×103 |
При обработке данных были применены следующие стати- стические критерии: Стьюдента – для проверки значимости ко- эффициентов уравнения регрессии; Фишера – для проверки адек- ватности регрессионного уравнения. В результате были получены уравнения, адекватно описывающие зависимости адгезионной прочности и эффективной вязкости теста от изучаемых факторов:
y1 = 7,79 − 0,59X1 + 0,54X 2 + 0,37X1 X 2 + 0,15X12 + 0,39X 22 ;
y2 = 4,84 ×103 + 0,26 ×103 X1 + 0,06 ×103 X 2 - 0,002 ×103 X1 X 2 - - 0,3×103 X12 + 0,19 ×103 X 22 .
Приведем регрессионные уравнения к каноническому виду. Для этого находим координаты центра из систем уравнений, по- лученных дифференцированием уравнений регрессии по X1 и X2, приравняв частные производные к нулю:
118

¶Y1 = -0,59 + 0,37X 2 + 0,3X1 = 0 ,
¶X1
¶Y1 = 0,54 + 0,37X1 + 0,78X 2 = 0
¶X2
откуда определяем X1s = 6,8 и X1s = -3,89 .
¶Y2 = 0,26×103 - 0,002×103 X 2 - 0,6×103 X1 = 0 ,
¶X1
¶Y2 = 0,06×103 - 0,002×103 X1 + 0,38×103 X 2 = 0
¶X2
откуда находим X1s = 0,44 и X1s = 0,16 .
Подставляя найденные значения в исходные уравнения,
вычисляем значения функций отклика в центре поверхности
Y1s = 4,73 и Y2s = 4,91×103 .
Составляя для каждого регрессионного уравнения характе- ристический полином, решая его, определяем корни. Для функ- ции отклика y1 имеем: B11 = 0,1 и B22 = 0,4 . В функции отклика y2
B11 = -0,34 и B22 = 0,20 .
Окончательно уравнения регрессии в канонической форме примут вид:
Y1 - 4,73 = 0,1Z12 + 0,4Z22 ,
Y2 - 4,91×103 = -0,31×103 Z12 + 0,2 ×103 Z22 .
Как видно из уравнений, исследуемые двумерные поверх- ности имеют вид эллипсоида и гиперболоида соответственно,
причем в центре эллипсоида имеет место минимум выходного параметра, на что указывает знак “+” перед каноническими ко- эффициентами. На рис. 3 и 4 представлены кривые равных значе- ний адгезионной прочности и эффективной вязкости теста в зави- симости от содержания ПАВ и pH воды, идущей на замес теста.
119
