2. Оценка валютных курсов

2.1 Выявление сезонных и циклических колебаний

Уровням рядов динамики валютною курса присущи периодические колебания внутри года, которые называют сезонными. Измерение «сезонной волны» способствует более полному анализу движении валютного курса. Исследование сезонности необходимо осуществить, используя помесячные или поквартальные данные.

Для измерения сезонных колебаний вычисляют индексы сезонности как отношение средней из фактических уровней по каждому из одноименных месяцев (кварталов) (Y_факт) к средней из выравненных уровней по таким же месяцам (кварталам) (Y_t):

.

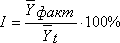Y_t можно рассчитать с помощью метода скользящей средней. Период скольжения для помесячных данных принимается равным 12 месяцам, для квартальных - 4. Для исключения сезонности фактические уровни делятся на соответствующие индексы сезонности. Также Y_t можно получить, используя аппроксимирующее уравнение. Часто применяют известный ряд Фурье. Устранение сезонности в этом случае достигается вычитанием Y_t из Y_факт

Характер движения валютного курса подчинен также закономерности, общей для всех экономических явлений рыночной экономики, - циклическому развитию когда подъемы периодически чередуются со спадами. Промежуток времени между двумя соседними вершинами (впадинами) составляет длину цикла. Величины отклонений значений от горизонтальной оси (например, вековой тенденции) характеризуют размах колебаний.

Для выявления циклической составляющей динамики валютного курса статистикой также используется выравнивание по ряду Фурье поскольку циклические колебания являются paзновидностью периодических, как и сезонные. Может применяться и метод скользящей средней. Период скольжения принимают, естественно, другой, соответствующий периоду циклических колебаний. Спектральной плотностью функции называется величина амплитуды гармоники в зависимости от ее периода. Чем больше амплитуда (спектр) данной гармоники, тем сильнее в использованной функции присутствуют колебания с этим периодом.

Помимо гармоник Фурье могут применяться и другие функции. Например, для поквартальных курсов немецкой марки (в ЭКЮ) за 1992 - 1994гг. получим уравнение параболы 4-го порядка:

y_t = 1,88-0,343t+0,103-0,011+0,0003

Целесообразно к исследованию циклических колебаний приступать, предварительно исключив из исходного ряда сезонность. Циклическую составляющую можно вычислить, если из фактических уровней исключить выравненные согласно основной тенденции и сезонную составляющую.

Y_цикл = Y-Y_t-Y_сезон,

Остановимся отдельно на часто применяемой для анализа движения валютного курса разновидности механического сглаживания - сглаживании по экспоненциальной средней.

Экспоненциальная средняя - разновидность взвешенной скользящей средней, которая чутко реагирует на любые изменения значений валютного курса. Она рассчитывается таким образом, что влияние на eе величину отдельных наблюдений следующее: чем дольше оно (наблюдение) отстоит от момента времени, на который рассчитывается средняя, тем меньшее значение оказывает.

Формула экспоненциальной средней такова:

,

где t - момент времени для которого исчисляется выравненное значение валютного курса;

- постоянная сглаживания (0<<1);

y_t - фактическое значение валютного курса в момент t;

- экспоненциальная средняя в момент времени, предшествующий t, можно принять для начального уровня y₁= или же среднее из прошлых значений

Если преобразовать приведенную выше рекурсивную формулу в более обобщенную, подставляя в уравнение последовательно вместо Y_t-1 предыдущее уравнение с Y_t-2 и т.д., то можно будет заметить, что перед наблюдением y_t-1 стоит вес (1-), перед y_t-1 стоит (1)² и т.д. Т. е. вес отдельного наблюдения убывает соответственно экспоненте по мере удаления наблюдения y_t в прошлое. Поэтому средняя и называется экспоненциальной. Дисперсия экспоненциальной средней равна:

,

где Д(y) - дисперсия уровней динамического ряда.

Чем меньше , тем Д() меньше, следовательно, более выравненным оказывается анализируемый ряд динамики.

Экспоненциальная средняя может использоваться для прогнозирования адаптивным методом, последовательно переходя к значениям в следующий момент времени.

Пример. Выравнивание по экспоненциальной средней курса рубля к доллару (обратная котировка) по реpультатам торгов на ММВБ за ноябрь 2012 года

Таблица 5. Выравнивание по экспоненциальной средней курса рубля к доллару

Дата торгов	t	Курс руб./долл. США, yt	Экспоненциальная средняя. Уt	Средняя поправка, yt-
1	2	3	4	5
4	1	30,90	30,9
5	2	30,84	30,8	0,14
6	3	31,40	30,98	0,42
10	4	31,32	30,84	0,48
11	5	31,41	30,96	0,55
12	6	31,57	30,88	0,69
13	7	31,43	30,8	0,63
16	8	31,21	30,56	0,65
17	9	31,06	30,89	0,83
18	10	30,96	30,52	0,44
19	11	30,91	30,49	0,42
20	12	30,73	30,35	0,38
23	13	30,84	30,44	0,40
24	14	30,66	30,31	0,35
25	15	30,85	30,47	0,38
26	16	30,89	30,50	0,39
27	17	31,12	30,61	0,51
30	18	31,26	30,72	0,54
31	19	31,46	30,81	0,65

Пусть для t=1 У_t=y_t=30,90; =0,2.

Тогда Y₂=0,2 · 30,84+ 0,8 · 30,92= 30,9;

Y₃= 0,2 · 30,40 +0,8 · 30,9 = 30,8;

Y₄ = 0,2 · 31,32+0,8 · 30,8 = 30,98.

Для t= 20 в качестве прогнозного значения принимается момент

t-1 =19, т.е. к моменту следующих торгов валютный курс прогнозируется согласно этой модели на уровне 30,96.