- •Информатика. Методы изучения. Основные компоненты
- •Лекция № 2
- •Лекция № 3 виды информации
- •Опосредованная информация
- •Лекция №4 описание и информация – описание
- •Лекция №5 данные
- •Переменные
- •Лекция №6 массивы
- •Информация-имитация
- •Лекция №7 кодирование информации
- •Системы счисления
- •Позиционные системы счисления
- •Лекция №8
- •Преобразование чисел позиционных систем из компактной в развернутую
- •Выполнение простейших действий над числами
- •Выполнение сложения позиционных чисел (чисел позиционных систем)
- •Выполнение вычитания чисел позиционных систем
- •Выполнение операции умножения (деления)
- •Выполнение арифметических действий в двоичной системе
- •Выполнение деления
- •Лекция №9 перевод чисел из одной системы счисления в другую
Лекция №8
Двенадцатиричная система:
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В12
Знаки: «+», «-».
Знаки разделителя: «,», «.».
Первые 25 целых положительных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1А, 1В, 2012.
Шестнадцатиричная система:
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D,E,F16.
Знаки: «+», «-».
Знаки разделителя: «,», «.».
Первые 35 целых положительных числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, A,B,C,D,E,F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, 2216.
Двоичная система:
Алфавит: 0, 12.
Знаки: «+», «-».
Знаки разделителя: «,», «.».
Первые 21 целых положительных чисел: 0, 1, 10, 11, 100, 101, 110, 11, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001, 10010, 10011, 101002.
Преобразование чисел позиционных систем из компактной в развернутую
Любое число любой позиционной системы может быть преобразовано из упрощенной (компактной) формы записи в развернутую (полную). Методика:
указать над каждой цифрой числа относительно разделителя ее разряд, начиная с нулевого, с последовательным увеличением на единицу со знаком «+» влево, со знаком «-» вправо;
определить в какой системе счисления представлено число и выбрать форму записи полинома, «родную» или десятичную;
сформировать значение полинома, начиная со старшего разряда.
Пример 1: число в десятичной системе 10265,310представить в виде полинома в «родной» (десятичной) системе.
![]()
Пример 2: число 10265,38представить в виде полиномов в «родной» и десятичной системах.
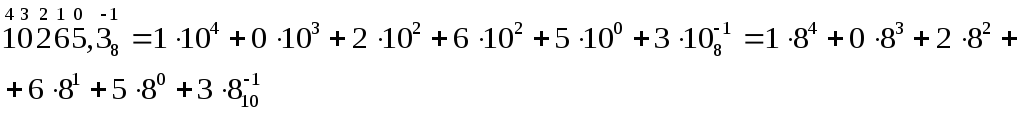
Пример 3: число 102,2213представить в виде полиномов в «родной» и десятичной системах.
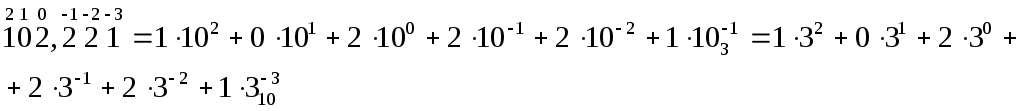
Выполнение простейших действий над числами
Основное достоинство всех позиционных систем счисления в том, что унифицированы правила не только компоновки и расшифровки, но и выполнения действий над их числами, поэтому знание одной из систем счисления позволяет сделать вывод о приемлемости правил этой системы для использования в любой другой. Основа обработки числовой информации – арифметические и логические действия над ними. Под арифметическими действиями понимается: сложение, вычитание, умножение, деление.
Выполнение сложения позиционных чисел (чисел позиционных систем)
Сложение – нахождение суммы значений элементов, участвующих в операции, т.е. операндов или слагаемых.
Количество слагаемых для одного действия должно быть не менее двух. Символ сложения – знак «+». Методика выполнения сложения:
записать слагаемые одно под другим поразрядно, дополняя недостающие разряду нулями;
выполнять операцию суммирования поразрядно, начиная с младшего разряда;
если результат (сумма цифр) меньше основания системы, то соответствующая цифра записывается в этот разряд;
если результат равен основанию системы, то в складываемом разряде записывается 0, а 1 переносится в левый, старший разряд;
если результат больше основания системы, то в складываемом разряде записывается цифра превышения основания, а единица переносится в ближайший левый разряд.
Примеры сложения одноразрядных чисел:
47 + 17
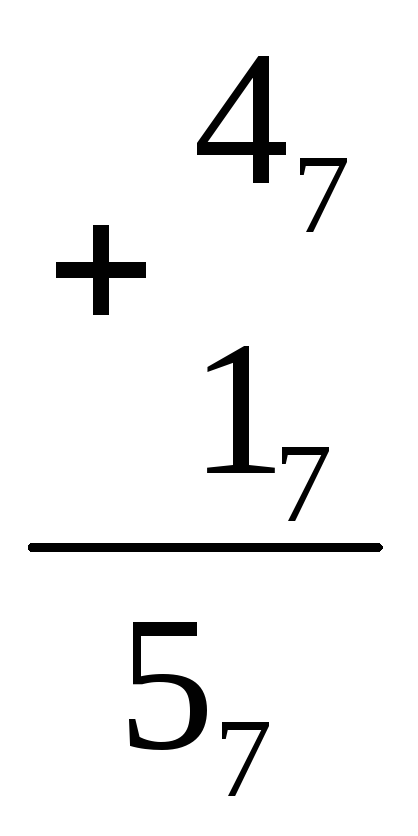
47 + 37
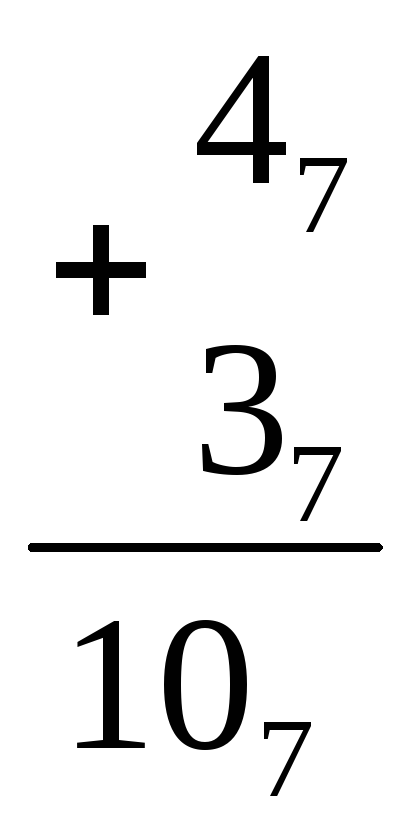
47+ 57