
FAJLOOBMENNIK-Obschaya_baza_v3_1
.doc
Если
молекула водорода, позитрон, протон
и ![]() -частица
имеют одинаковую длину волны де Бройля,
то наибольшей скоростью обладает …
позитрон
-частица
имеют одинаковую длину волны де Бройля,
то наибольшей скоростью обладает …
позитрон
Решение:
Длина
волны де Бройля определяется
формулой ![]() ,
где
,
где ![]() –
постоянная Планка,
–
постоянная Планка, ![]() и
и ![]() –
масса и скорость частицы. Отсюда скорость
частицы равна
–
масса и скорость частицы. Отсюда скорость
частицы равна ![]() .
По условию задания
.
По условию задания ![]() ,
следовательно,
,
следовательно, ![]() .
Тогда наибольшей скоростью обладает
частица с наименьшей массой. Известно,
что
.
Тогда наибольшей скоростью обладает
частица с наименьшей массой. Известно,
что ![]() .
Следовательно, наибольшей скоростью
обладает позитрон.
.
Следовательно, наибольшей скоростью
обладает позитрон.
На
зеркальную поверхность площадью ![]() по
нормали к ней ежесекундно падает
по
нормали к ней ежесекундно падает ![]() фотонов.
Если при этом световое давление равно
фотонов.
Если при этом световое давление равно ![]() ,
то длина волны (в нм)
падающего света равна … 663
,
то длина волны (в нм)
падающего света равна … 663
Решение:
Давление,
производимое светом при нормальном
падении, определяется по формуле: ![]() ,
где
,
где ![]() энергетическая
освещенность поверхности, равная
энергии, падающей на единицу площади
поверхности в единицу времени;
энергетическая
освещенность поверхности, равная
энергии, падающей на единицу площади
поверхности в единицу времени; ![]() скорость
света;
скорость
света; ![]() коэффициент
отражения. Энергетическая освещенность
поверхности
коэффициент
отражения. Энергетическая освещенность
поверхности ![]() ,
где
,
где ![]() –
число фотонов, падающих на поверхность
площадью
–
число фотонов, падающих на поверхность
площадью ![]() в
единицу времени. Тогда
в
единицу времени. Тогда ![]() Отсюда
Отсюда  Здесь
учтено, что для зеркальной поверхности
Здесь
учтено, что для зеркальной поверхности ![]() .
.
Уединенный
медный шарик освещается ультрафиолетовым
излучением с длиной волны ![]() .
Если работа выхода электрона для меди
.
Если работа выхода электрона для меди ![]() ,
то максимальный потенциал, до которого
может зарядиться шарик, равен __3,0___ В.
(
,
то максимальный потенциал, до которого
может зарядиться шарик, равен __3,0___ В.
(![]()
![]() )
)
Законом
сохранения электрического
заряда запрещен процесс,
описываемый уравнением …![]()
Решение:
При
взаимодействии элементарных частиц и
их превращениях возможны только такие
процессы, в которых выполняются законы
сохранения, в частности закон сохранения
электрического заряда: суммарный
электрический заряд частиц, вступающих
в реакцию, равен суммарному электрическому
заряду частиц, полученных в результате
реакции. Электрический заряд ![]() в
единицах элементарного заряда равен:
у нейтрона
в
единицах элементарного заряда равен:
у нейтрона ![]()
![]() ;
протона
;
протона ![]()
![]() ;
электрона
;
электрона ![]()
![]() ;
позитрона
;
позитрона ![]()
![]() ;
электронного нейтрино и антинейтрино
(
;
электронного нейтрино и антинейтрино
(![]() ,
,![]() )
) ![]() ;
антипротона
;
антипротона ![]()
![]() ;
мюонного нейтрино
;
мюонного нейтрино ![]()
![]() ;
мюона
;
мюона ![]()
![]() .
Закон сохранения электрического заряда
не выполняется в реакции
.
Закон сохранения электрического заряда
не выполняется в реакции ![]() .
.
Законом
сохранения электрического заряда
разрешена реакция …![]()
Решение:
При
взаимодействии элементарных частиц и
их превращениях возможны только такие
процессы, в которых выполняются законы
сохранения, в частности закон сохранения
электрического заряда: суммарный
электрический заряд частиц, вступающих
в реакцию, равен суммарному электрическому
заряду частиц, полученных в результате
реакции. Электрический заряд ![]() в
единицах элементарного заряда равен:
у нейтрона (
в
единицах элементарного заряда равен:
у нейтрона (![]() )
) ![]() ;
протона (
;
протона (![]() )
) ![]() ;
электрона (
;
электрона (![]() )
) ![]() ;
позитрона (
;
позитрона (![]() )
) ![]() ;
электронного нейтрино и антинейтрино
(
;
электронного нейтрино и антинейтрино
(![]() ,
,![]() )
) ![]() ;
антипротона (
;
антипротона (![]() )
) ![]() ;
мюонного нейтрино (
;
мюонного нейтрино (![]() )
) ![]() ;
мюона (
;
мюона (![]() )
) ![]() .
Закон сохранения электрического заряда
выполняется в реакции
.
Закон сохранения электрического заряда
выполняется в реакции
![]()
Установите соответствие между переносчиками фундаментальных взаимодействий и видами этих взаимодействий. 1. Фотоны 2. Глюоны 3. Бозоны
|
1 |
электромагнитное |
|
2 |
сильное |
|
3 |
слабое |
Решение:
Все
фундаментальные взаимодействия имеют
обменный характер. В качестве элементарных
актов каждого взаимодействия выступают
процессы испускания и поглощения данной
частицей ![]() некоторой
частицы
некоторой
частицы ![]() как
раз и определяющей тип данного
взаимодействия. Сама частица
как
раз и определяющей тип данного
взаимодействия. Сама частица ![]() может
остаться неизменной, а может превратиться
в некоторую другую частицу
может
остаться неизменной, а может превратиться
в некоторую другую частицу ![]() :
: ![]() Расположенная
поблизости частица
Расположенная
поблизости частица ![]() также
способна поглощать и испускать
частицу
также
способна поглощать и испускать
частицу ![]() :
: ![]() Если
Если ![]() испустит
испустит ![]() ,
а
,
а ![]() поглотит
поглотит ![]() или
наоборот, то промежуточная частица
или
наоборот, то промежуточная частица ![]() исчезнет,
а между
исчезнет,
а между ![]() ,
, ![]() и
и ![]() ,
, ![]() возникнет
взаимодействие, которое приведет к
превращению
возникнет
взаимодействие, которое приведет к
превращению ![]() Частица
Частица ![]() является
переносчиком данного взаимодействия.
Переносчики электромагнитного
взаимодействия − фотоны. Переносчики
сильного взаимодействия – глюоны,
осуществляющие связь между кварками,
из которых состоят протоны и нейтроны.
Переносчиками слабого взаимодействия
являются промежуточные бозоны. Переносчики
гравитационного взаимодействия –
гравитоны (экспериментально пока не
обнаружены).
является
переносчиком данного взаимодействия.
Переносчики электромагнитного
взаимодействия − фотоны. Переносчики
сильного взаимодействия – глюоны,
осуществляющие связь между кварками,
из которых состоят протоны и нейтроны.
Переносчиками слабого взаимодействия
являются промежуточные бозоны. Переносчики
гравитационного взаимодействия –
гравитоны (экспериментально пока не
обнаружены).
Показатель
преломления среды, в которой распространяется
электромагнитная волна с напряженностями
электрического и магнитного полей
соответственно ![]() и
объемной плотностью энергии
и
объемной плотностью энергии  ,
равен …2
,
равен …2
Решение:
Плотность
потока энергии электромагнитной волны
(вектор Умова – Пойнтинга) равна:  .
Также
.
Также ![]() где
где ![]() объемная
плотность энергии,
объемная
плотность энергии, ![]() скорость
электромагнитной волны в среде,
скорость
электромагнитной волны в среде, ![]() скорость
электромагнитной волны в вакууме,
скорость
электромагнитной волны в вакууме, ![]() показатель
преломления. Следовательно,
показатель
преломления. Следовательно, ![]() и
и 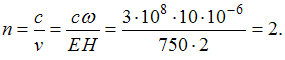
На
рисунке показана кварковая диаграмма
захвата нуклоном ![]() -мезона.
-мезона.
 Эта
диаграмма соответствует реакции …
Эта
диаграмма соответствует реакции …![]()
Решение:
Кварковый
состав ![]() соответствует
протону
соответствует
протону ![]() с
зарядом +1, полуцелым спином. Протон
относится к обычным барионам класса
адронов. Кварковый состав
с
зарядом +1, полуцелым спином. Протон
относится к обычным барионам класса
адронов. Кварковый состав ![]() соответствует
нейтрону
соответствует
нейтрону ![]() с
зарядом 0, полуцелым спином. Нейтрон
относится к обычным барионам класса
адронов. Протоны и нейтроны называют
нуклонами. При захвате протоном
с
зарядом 0, полуцелым спином. Нейтрон
относится к обычным барионам класса
адронов. Протоны и нейтроны называют
нуклонами. При захвате протоном ![]() -мезона
протон превращается в нейтрон и
испускается мюонное нейтрино, заряд
которого равен 0. При превращении
элементарных частиц выполняются законы
сохранения, в частности закон сохранения
электрического заряда. Этот закон
выполняется в реакции
-мезона
протон превращается в нейтрон и
испускается мюонное нейтрино, заряд
которого равен 0. При превращении
элементарных частиц выполняются законы
сохранения, в частности закон сохранения
электрического заряда. Этот закон
выполняется в реакции ![]() .
.
![]() -мезон,
двигавшийся со скоростью
-мезон,
двигавшийся со скоростью ![]() (с –
скорость света в вакууме) в лабораторной
системе отсчета, распадается на два
фотона: 1 и 2.
В системе отсчета мезона фотон 1 был
испущен вперед, а фотон 2 –
назад относительно направления полета
мезона. Скорость фотона 1 в
лабораторной системе отсчета равна
…
(с –
скорость света в вакууме) в лабораторной
системе отсчета, распадается на два
фотона: 1 и 2.
В системе отсчета мезона фотон 1 был
испущен вперед, а фотон 2 –
назад относительно направления полета
мезона. Скорость фотона 1 в
лабораторной системе отсчета равна
…![]() Решение:
Фотон
является частицей, которая может
существовать, только двигаясь со
скоростью с,
то есть со скоростью света в вакууме.
Кроме того, согласно одному из постулатов
специальной теории относительности –
принципу постоянства скорости света –
скорость света в вакууме не зависит от
движения источника света и, следовательно,
одинакова во всех инерциальных системах
отсчета. Поэтому скорость фотона 1 с
учетом направления его движения в
лабораторной системе отсчета равна
Решение:
Фотон
является частицей, которая может
существовать, только двигаясь со
скоростью с,
то есть со скоростью света в вакууме.
Кроме того, согласно одному из постулатов
специальной теории относительности –
принципу постоянства скорости света –
скорость света в вакууме не зависит от
движения источника света и, следовательно,
одинакова во всех инерциальных системах
отсчета. Поэтому скорость фотона 1 с
учетом направления его движения в
лабораторной системе отсчета равна ![]() .
.
![]() -распадом
является ядерное превращение, происходящее
по схеме …
-распадом
является ядерное превращение, происходящее
по схеме …![]() Решение:
При
Решение:
При ![]() -распаде
в ядре происходит превращение протона
в нейтрон с испусканием позитрона и
электронного нейтрино:
-распаде
в ядре происходит превращение протона
в нейтрон с испусканием позитрона и
электронного нейтрино: ![]() .
.
Сила
тока в проводящем круговом контуре
индуктивностью 100 мГн изменяется
с течением времени по
закону ![]() (в
единицах СИ):
(в
единицах СИ):
 Абсолютная
величина ЭДС самоиндукции в момент
времени 2 с равна
____ ; при этом индукционный ток
направлен …0,12 В;
против часовой стрелки
Абсолютная
величина ЭДС самоиндукции в момент
времени 2 с равна
____ ; при этом индукционный ток
направлен …0,12 В;
против часовой стрелки
Решение:
ЭДС
самоиндукции, возникающая в контуре
при изменении в нем силы тока I,
определяется по формуле: ![]() ,
где L –
индуктивность контура. Знак минус в
формуле соответствует правилу Ленца:
индукционный ток направлен так, что
противодействует изменению тока в цепи:
замедляет его возрастание или убывание.
Таким образом, ЭДС самоиндукции равна
,
где L –
индуктивность контура. Знак минус в
формуле соответствует правилу Ленца:
индукционный ток направлен так, что
противодействует изменению тока в цепи:
замедляет его возрастание или убывание.
Таким образом, ЭДС самоиндукции равна ![]() .
Абсолютная величина ЭДС самоиндукции
равна
.
Абсолютная величина ЭДС самоиндукции
равна ![]() ,
индукционный ток направлен против
часовой стрелки. При этом учтено
направление тока в контуре и его
возрастание со временем (что следует
из заданного закона изменения силы
тока).
,
индукционный ток направлен против
часовой стрелки. При этом учтено
направление тока в контуре и его
возрастание со временем (что следует
из заданного закона изменения силы
тока).
Электростатическое
поле создано бесконечной равномерно
заряженной плоскостью (![]() – поверхностная
плотность зарядов).
– поверхностная
плотность зарядов).
 Градиент
потенциала поля в точке А ориентирован
в направлении …3
Градиент
потенциала поля в точке А ориентирован
в направлении …3
Решение:
Градиент
потенциала в некоторой точке связан с
напряженностью поля в этой точке
соотношением ![]() ,
поэтому для нахождения направления
,
поэтому для нахождения направления ![]() в
точке А необходимо найти направление
вектора напряженности поля в этой точке.
Вектор напряженности поля бесконечной
равномерно заряженной плоскости
направлен перпендикулярно плоскости.
Если
в
точке А необходимо найти направление
вектора напряженности поля в этой точке.
Вектор напряженности поля бесконечной
равномерно заряженной плоскости
направлен перпендикулярно плоскости.
Если ![]() ,
вектор
,
вектор ![]() направлен
к плоскости, а вектор
направлен
к плоскости, а вектор ![]() –
от нее, то есть в направлении 3.
–
от нее, то есть в направлении 3.
При
поступлении в неизолированную
термодинамическую систему тепла в ходе
обратимого процесса для приращения
энтропии верным будет
соотношение …![]() Решение:
Отношение
Решение:
Отношение ![]() в
обратимом процессе есть полный
дифференциал функции состояния системы,
называемой энтропией
в
обратимом процессе есть полный
дифференциал функции состояния системы,
называемой энтропией ![]() системы:
системы:  .
В изолированных системах энтропия не
может убывать при любых, происходящих
в ней процессах:
.
В изолированных системах энтропия не
может убывать при любых, происходящих
в ней процессах: ![]() .
Знак равенства относится к обратимым
процессам, а знак «больше» – к необратимым
процессам. Если в неизолированную
систему поступает тепло и происходит
необратимый процесс, то энтропия
возрастает за счет не только полученного
тепла, но и необратимости процесса:
.
Знак равенства относится к обратимым
процессам, а знак «больше» – к необратимым
процессам. Если в неизолированную
систему поступает тепло и происходит
необратимый процесс, то энтропия
возрастает за счет не только полученного
тепла, но и необратимости процесса: ![]() .
.
Два одинаковых источника тока соединены последовательно. Если источники соединить параллельно, то сила тока короткого замыкания … увеличится в 2 раза
Решение:
Сила
тока короткого замыкания  ,
где
,
где ![]() и
и ![]() –
ЭДС и внутреннее сопротивление батареи,
состоящей из двух источников. При
последовательном соединении
источников
–
ЭДС и внутреннее сопротивление батареи,
состоящей из двух источников. При
последовательном соединении
источников ![]() ,
, ![]() ;
здесь
;
здесь ![]() и
и ![]() –
ЭДС и внутреннее сопротивление одного
источника. При параллельном соединении
–
ЭДС и внутреннее сопротивление одного
источника. При параллельном соединении ![]() ,
а
,
а ![]() .
Тогда
.
Тогда ![]() ,
, ![]() .
.
Поле
создано прямолинейным длинным проводником
с током I1.
Если отрезок проводника с током I2 расположен
в одной плоскости с длинным проводником
так, как показано на рисунке, то сила
Ампера …
лежит
в плоскости чертежа и направлена влево

Решение: На проводник с током в магнитном поле действует сила Ампера. В данном случае магнитное поле создается прямолинейным длинным проводником с током I1. В соответствии с правилом правого винта (буравчика) вектор магнитной индукции в месте расположения отрезка проводника с током I2направлен перпендикулярно плоскости чертежа «от нас». В случае прямолинейного отрезка проводника с током в перпендикулярном проводнику магнитном поле для нахождения направления силы Ампера удобно воспользоваться правилом левой руки, согласно которому сила Ампера лежит в плоскости чертежа и направлена влево.
При
комнатной температуре отношение ![]() молярных
теплоемкостей при постоянном давлении
и постоянном объеме равно
молярных
теплоемкостей при постоянном давлении
и постоянном объеме равно ![]() для …
кислорода
для …
кислорода
Решение:
Из
отношения 
![]() найдем
найдем ![]() ,
, ![]() .
Так как 3 поступательные и 2 вращательные
степени свободы имеют двухатомные газы,
следовательно, это кислород.
.
Так как 3 поступательные и 2 вращательные
степени свободы имеют двухатомные газы,
следовательно, это кислород.
На
рисунке схематически изображен цикл
Карно в координатах ![]() :
:
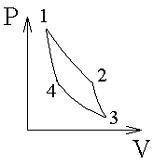 Увеличение
энтропии имеет место на участке …1–2
Увеличение
энтропии имеет место на участке …1–2
Решение:
Цикл
Карно состоит из двух изотерм и двух
адиабат (изотермического расширения
1–2, адиабатного расширения 2–3,
изотермического сжатия 3–4 и адиабатного
сжатия 4–1). Энтропия ![]() определяется
соотношением
определяется
соотношением ![]() ,
где
,
где ![]() –
количество теплоты, сообщаемое системе.
В адиабатном процессе энтропия не
изменяется, так как адиабатный процесс
протекает без теплообмена с окружающей
средой. Для изотермического процесса,
согласно первому началу термодинамики,
–
количество теплоты, сообщаемое системе.
В адиабатном процессе энтропия не
изменяется, так как адиабатный процесс
протекает без теплообмена с окружающей
средой. Для изотермического процесса,
согласно первому началу термодинамики, ![]() .
При расширении работа газа положительна.
Следовательно, изотермическое расширение
происходит за счет теплоты, получаемой
рабочим телом. Поэтому при изотермическом
расширении
.
При расширении работа газа положительна.
Следовательно, изотермическое расширение
происходит за счет теплоты, получаемой
рабочим телом. Поэтому при изотермическом
расширении ![]() ,
то есть увеличение энтропии имеет место
на участке
,
то есть увеличение энтропии имеет место
на участке ![]() .
.
На
рисунке схематически изображен цикл
Карно в координатах ![]() :
:
 Уменьшение
энтропии имеет место на участке …3-4
Уменьшение
энтропии имеет место на участке …3-4
Решение:
Цикл
Карно состоит из двух изотерм и двух
адиабат (изотермического расширения 1–2,
адиабатного расширения 2–3,
изотермического сжатия 3–4 и адиабатного
сжатия 4–1). Энтропия ![]() определяется
соотношением
определяется
соотношением ![]() ,
где
,
где ![]() –
количество теплоты, сообщаемое системе.
В адиабатном процессе энтропия не
изменяется, так как адиабатный процесс
протекает без теплообмена с окружающей
средой. Для изотермического процесса
согласно первому началу термодинамики
–
количество теплоты, сообщаемое системе.
В адиабатном процессе энтропия не
изменяется, так как адиабатный процесс
протекает без теплообмена с окружающей
средой. Для изотермического процесса
согласно первому началу термодинамики ![]() .
При сжатии работа газа отрицательна.
Следовательно, при изотермическом
сжатии рабочее тело отдает теплоту.
Поэтому при изотермическом сжатии
.
При сжатии работа газа отрицательна.
Следовательно, при изотермическом
сжатии рабочее тело отдает теплоту.
Поэтому при изотермическом сжатии ![]() ,
то есть уменьшение энтропии имеет место
на участке 3–4.
,
то есть уменьшение энтропии имеет место
на участке 3–4.
Если КПД цикла Карно равен 60%, то температура нагревателя больше температуры холодильника в ___2,5___ раз(а).
Решение:
КПД
обратимого цикла Карно равен:  ,
или
,
или  ;
следовательно,
;
следовательно,  ;
отсюда
;
отсюда  и
и 
Для -распада несправедливым является
утверждение, что …
вылетающие
из ядра ![]() -частицы
могут иметь любую энергию
-частицы
могут иметь любую энергию ![]() Решение:
-распадом
называется испускание ядрами некоторых
химических элементов -частиц,
представляющих собой ядра атомов гелия.
Уравнение -распада
имеет вид:
Решение:
-распадом
называется испускание ядрами некоторых
химических элементов -частиц,
представляющих собой ядра атомов гелия.
Уравнение -распада
имеет вид: ![]() ,
где
,
где ![]() –
ядро, подверженное распаду, или
«родительское» ядро,
–
ядро, подверженное распаду, или
«родительское» ядро, ![]() –
ядро, образующееся в результате распада,
или «дочернее» ядро. -распад
является свойством тяжелых ядер с
массовыми числами
–
ядро, образующееся в результате распада,
или «дочернее» ядро. -распад
является свойством тяжелых ядер с
массовыми числами ![]() и
зарядовыми числами
и
зарядовыми числами ![]() .
Исследования показали, что у
каждого -излучающего
ядра имеется несколько групп
«моноэнергетических»
.
Исследования показали, что у
каждого -излучающего
ядра имеется несколько групп
«моноэнергетических» ![]() -частиц,
что свидетельствует о дискретности
энергетического спектра ядер.
-частиц,
что свидетельствует о дискретности
энергетического спектра ядер.
Складываются
взаимно перпендикулярные колебания.
Установите соответствие между формой
траектории и законами колебания
точки ![]() вдоль
осей координат
вдоль
осей координат ![]()
![]() 1.
Прямая линия
2. Окружность
3. Фигура
Лиссажу
1.
Прямая линия
2. Окружность
3. Фигура
Лиссажу
|
1 |
|
|
2 |
|
|
3 |
|
Решение:
При
одинаковой частоте колебаний вдоль
осей ![]()
![]() исключив
параметр времени, можно получить
уравнение траектории:
исключив
параметр времени, можно получить
уравнение траектории:  .
Если разность фаз колебаний
.
Если разность фаз колебаний ![]() ,
то уравнение преобразуется к виду
,
то уравнение преобразуется к виду  ,
или
,
или  ,
что соответствует уравнению
прямой:
,
что соответствует уравнению
прямой:  .
Если
.
Если ![]() ,
то
,
то  ,
что является уравнением эллипса, причем
если амплитуды равны
,
что является уравнением эллипса, причем
если амплитуды равны ![]() ,
то это будет уравнение окружности.
Если
складываются колебания с циклическими
частотами
,
то это будет уравнение окружности.
Если
складываются колебания с циклическими
частотами ![]() и
и ![]() ,
где
,
где ![]() и
и ![]() целые
числа, точка
целые
числа, точка ![]() описывает
сложную кривую, которую называют фигурой
Лиссажу. Форма кривой зависит от
соотношения амплитуд, частот и начальных
фаз складываемых колебаний.
описывает
сложную кривую, которую называют фигурой
Лиссажу. Форма кривой зависит от
соотношения амплитуд, частот и начальных
фаз складываемых колебаний.



