FAJLOOBMENNIK-Obschaya_baza_v3_1

Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами . Установите соответствие междуразностью фаз складываемых колебаний и амплитудой результирующего колебания. 1.   2.  3.   0

1
2
3

Решение: Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле ,  где и  – амплитуды, () – разность фаз складываемых колебаний.  Если разность фаз , , то  и .  Если , , то .  Если , , то .

Складываются два гармонических колебания одного направления с одинаковыми частотами и амплитудами, равными  и . Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний. 1.  2.  3. 

1
2
3

Решение: Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле , где и  – амплитуды складываемых колебаний, () – разность их фаз. Если амплитуда результирующего колебания , то . Тогда  и разность фаз складываемых колебаний равна . Если , то . Тогда , следовательно, . Если , то . Тогда , следовательно, .

Уравнение бегущей волны имеет вид: , где  выражено в миллиметрах,  – в секундах,  – в метрах. Отношение амплитудного значения скорости частиц среды к скорости распространения волны равно …0,028

Решение: Уравнение плоской гармонической волны, распространяющейся вдоль оси ОХ, имеет вид: . Здесь  – амплитуда волны, () – ее фаза, начальная фаза,  – циклическая частота, – волновое число. Из сопоставления с уравнением, приведенным в условии, следует: , , , . Для волнового числа справедливо соотношение , где  – длина волны, – скорость ее распространения. Отсюда скорость распространения волны равна . Скорость колебаний частиц среды , откуда амплитуда скорости равна . Тогда искомое отношение равно .

На рисунке показана ориентация векторов напряженности электрического  и магнитного  полей в электромагнитной волне. Вектор Умова – Пойнтинга ориентирован в направлении …3

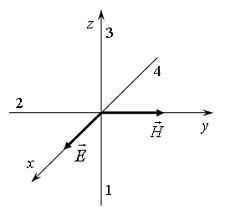
Решение: Вектор Умова – Пойнтинга (вектор плотности потока энергии электромагнитного поля) равен векторному произведению: , где  и  – векторы напряженностей электрического и магнитного полей электромагнитной волны соответственно. Векторы , , образуют правую тройку векторов. Следовательно, вектор Умова – Пойнтинга ориентирован в направлении 3.

На рисунке показана ориентация векторов напряженности электрического () и магнитного () полей в электромагнитной волне. Вектор плотности потока энергии электромагнитного поля ориентирован в направлении … 4

На рисунке представлена зависимость плотности тока j, протекающего в проводниках 1 и 2, от напряженности электрического поля Е:

Отношение удельных сопротивлений ₁/₂ этих проводников равно … Решение: Согласно закону Ома в дифференциальной форме, плотность тока в проводнике равна , где  – удельное сопротивление материала, – напряженность электрического поля в проводнике. Взяв любое значение напряженности поля, например,  и соответствующие ему значения плотности тока из графика  и , можно определить отношение удельных сопротивлений проводников: .

Электростатическое поле создано  положительно заряженной сферой. Правильно отражает зависимость потенциала от расстояния рисунок … 2

Решение: Потенциал поля на поверхности и внутри заряженной металлической сферы является постоянным, вне сферы убывает с расстоянием r по такому же закону, как для точечного заряда. Таким образом, график зависимости  для заряженной металлической сферы радиусом R показан на рисунке 2.

Рамка с током с магнитным дипольным моментом , направление которого указано на рисунке, находится в однородном магнитном поле: Момент сил, действующих на магнитный диполь, направлен … перпендикулярно плоскости рисунка к нам

Решение: На контур с током в однородном магнитном поле действует вращающий момент сил , стремящийся расположить контур таким образом, чтобы вектор его магнитного момента  был сонаправлен с вектором магнитной индукции  поля. Используя определение векторного произведения, находим, что момент сил направлен перпендикулярно плоскости рисунка к нам.

Проводящая рамка вращается с постоянной угловой скоростью в однородном магнитном поле вокруг оси, лежащей в плоскости рамки и перпендикулярной вектору индукции  (см. рис.). На рисунке также представлен график зависимости от времени потока вектора магнитной индукции, пронизывающего рамку. Если максимальное значение магнитного потока  мВб, сопротивление рамки  Ом, а время измерялось в секундах, то закон изменения со временем силы индукционного тока имеет вид …

Решение: Сила индукционного тока , где  – ЭДС индукции, R – сопротивление рамки. В соответствии с законом Фарадея для электромагнитной индукции. Чтобы найти закон изменения ЭДС индукции со временем, необходимо знать зависимость от времени магнитного потока, пронизывающего рамку. Из приведенного графика следует, что , поскольку  Тогда , а 

На пути естественного света помещены две пластинки турмалина. После прохождения пластинки 1 свет полностью поляризован. Если J₀ – интенсивность естественного света, а J₁ и J₂ – интенсивности света, прошедшего пластинки соответственно 1 и 2, то при угле  между направлениями OO и O’O’, равном 30°, J₂ и J₀ связаны соотношением …

Решение: Если J₀ – интенсивность естественного света, то в отсутствие поглощения интенсивность J₁ света, прошедшего через поляризатор (пластинку 1), равна , а интенсивность J₂ света, прошедшего через анализатор (пластинку 2), определяется законом Малюса: .

На рисунке представлены графики, отражающие характер зависимости поляризованности Р диэлектрика от напряженности внешнего электрического поля Е. 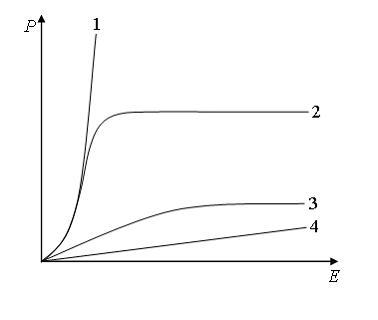 Неполярным диэлектрикам соответствует кривая …4

Решение:

К неполярным диэлектрикам относятся диэлектрики, в молекулах (атомах) которых в отсутствие внешнего электрического поля «центры тяжести» положительных и отрицательных зарядов совпадают и дипольные моменты таких молекул равны нулю. При внесении неполярного диэлектрика во внешнее электрическое поле происходит деформация электронных оболочек атомов и молекул. «Центры тяжести» положительных и отрицательных зарядов смещаются друг относительно друга. Вследствие этого неполярная молекула приобретает во внешнем электрическом поле индуцированный дипольный момент, направленный вдоль поля и пропорциональный напряженности  внешнего поля (этот механизм поляризации диэлектриков получил название электронной или деформационной поляризации). Тепловое движение неполярных молекул не влияет на возникновение у них индуцированных электрических дипольных моментов. Таким образом, для неполярных диэлектриков характерна прямо пропорциональная зависимость поляризованности от напряженности внешнего электрического поля, что отражает кривая 4.

На рисунке представлены графики, отражающие характер зависимости величины намагниченности I вещества (по модулю) от напряженности магнитного поля Н: Парамагнетикам соответствует кривая … 3

Решение: К парамагнетикам относятся вещества, атомы (молекулы) которых обладают собственным магнитным моментом. Однако вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно в отсутствие внешнего магнитного поля, и намагниченность вещества в этих условиях равна нулю. При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов (молекул) в направлении поля. Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающее его. Диамагнитный эффект наблюдается и в парамагнетиках, но он значительно слабее парамагнитного и поэтому остается незаметным. Магнитная восприимчивость парамагнетиков положительна, значительно меньше единицы и составляет величину . В слабом магнитном поле намагниченность пропорциональна напряженности внешнего поля. В очень сильном магнитном поле (и при достаточно низкой температуре) магнитные моменты всех молекул располагаются практически параллельно полю. При этом намагниченность парамагнетика достигает максимального значения (но существенно меньшего по сравнению с ферромагнетиками). Парамагнетикам соответствует кривая 3.

Протон влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции и начинает двигаться по окружности. При увеличении кинетической энергии протона (если ) в 4 раза радиус окружности … увеличится в 2 раза

Контур площадью  м²  расположен перпендикулярно к линиям магнитной индукции. Магнитная индукция изменяется по закону . ЭДС индукции, возникающая в контуре, изменяется по закону …

Электропроводка должна выполняться из достаточно толстого провода, чтобы он сильно не нагревался и не создавал угрозы пожара. Если проводка рассчитана на максимальную силу тока 16 А и на погонном метре провода должно выделяться не более 2 Вт тепла, то диаметр медного провода (с учетом того, что удельное сопротивление меди равно 17 нОм·м) равен ___1,7___ мм.

Парамагнетиком является вещество с магнитной проницаемостью …=1,00036

Решение: Все вещества можно разделить на слабомагнитные (парамагнетики и диамагнетики) и сильномагнитные (ферромагнетики). У парамагнетиков магнитная проницаемость >1, у диамагнетиков <1, причем как у тех, так и у других  мало отличается от единицы, то есть магнитные свойства этих магнетиков выражены очень слабо. Поэтому парамагнетиком среди перечисленных веществ является вещество с магнитной проницаемостью =1,00036.

Диамагнетиком является вещество с магнитной проницаемостью …=0,999864

В некоторой области пространства создано электростатическое поле, потенциал которого описывается функцией . Вектор напряженности электрического поля в точке пространства, показанной на рисунке, будет иметь направление …4

Решение: Связь напряженности и потенциала электростатического поля имеет вид: , или в проекциях на оси прямоугольной декартовой системы координат: , , . Так как по условию потенциал  зависит только от х, значит, отлична от нуля только проекция вектора напряженности . Таким образом, вектор напряженности электрического поля будет иметь направление, показанное стрелкой 4.

Физический смысл уравнения Максвелла  заключается в следующем … источником электрического поля являются свободные электрические заряды Решение: Данное уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде –  источником электрического поля являются свободные электрические заряды. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.

Обобщением теоремы Остроградского – Гаусса для электростатического поля в среде является уравнение …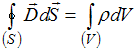 Решение: Уравнение Максвелла  является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде – источником электрического поля являются свободные электрические заряды. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.

Физический смысл уравнения  Максвелла  заключается в следующем … «магнитных зарядов» не существует: силовые линии магнитного поля замкнуты

Решение: Уравнение Максвелла  означает, что в природе нет магнитных зарядов, на которых начинались бы или заканчивались линии магнитной индукции.

Физический смысл уравнения Максвелла  заключается в следующем … изменяющееся со временем магнитное поле порождает вихревое электрическое поле

Решение: Уравнение Максвелла  означает, что с переменным магнитным полем неразрывно связано вихревое электрическое поле.

Физический смысл уравнения Максвелла  заключается в следующем … источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле Решение: Из уравнения Максвелла  следует, что переменное электрическое поле, наряду с токами проводимости, является источником вихревого магнитного поля.

Уравнения Максвелла являются основными законами классической макроскопической электродинамики, сформулированными на основе обобщения важнейших законов электростатики и электромагнетизма. Эти уравнения в интегральной форме имеют вид: 1).; 2).; 3).; 4). 0. Третье уравнение Максвелла является обобщением … теоремы Остроградского – Гаусса для электростатического поля в среде Решение: Третье уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.

Уравнения Максвелла являются основными законами классической макроскопической электродинамики, сформулированными на основе обобщения важнейших законов электростатики и электромагнетизма. Эти уравнения в интегральной форме имеют вид: 1).; 2).; 3).; 4). 0. Четвертое уравнение Максвелла является обобщением … теоремы Остроградского – Гаусса для магнитного поля Решение: Четвертое уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для магнитного поля. Максвелл предположил, что она справедлива для любого магнитного поля (в вакууме или в среде, стационарного и переменного).

Полная система уравнений Максвелла для электромагнитного поля в интегральной форме имеет вид: , , ,  0. Следующая система уравнений: , , ,  0 – справедлива для … электромагнитного поля при наличии заряженных тел и в отсутствие токов проводимости Решение: Вторая система уравнений отличается от первой системы своими первым и  вторым уравнениями. В первом уравнении  иначе записана правая часть, но , а во втором уравнении отсутствует в подынтегральном выражении плотность тока проводимости  и не конкретизирована плотность тока смещения (). 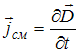Отсутствие токов проводимости означает, что источником вихревого магнитного поля является только переменное электрическое поле. Таким образом, рассматриваемая система справедлива для переменного электромагнитного поля при наличии заряженных тел и в отсутствие токов проводимости.

Утверждение «Переменное электрическое поле, наряду с электрическим током, является источником магнитного поля» раскрывает физический смысл уравнения …