
13
.docВведение.
В данной лекции продолжается изучение темы «Неопределенный интеграл», включающей три лекции, три практических занятия и одно лабораторное занятие. Данная лекция продолжает изучение фундаментального вопроса математического анализа: неопределенного интеграла. И. Ньютон и Г. Лейбниц независимо друг от друга нашли общий метод для нахождения первообразных функций, построили логические основы дифференциального и интегрального исчисления. Строгое изложение теории интегрирования появилось в прошлом веке. Решение этой проблемы тесно связано с именами О. Коши, Б. Римана, Г. Дарбу. Обобщения понятия интеграла в начале нашего столетия были предложены французскими математиками А. Лебегом, А. Данжуа, советским математиком А. Хинчиным. Лекция продолжает изучение методов интегрирования.
-
Интегрирование некоторых иррациональных
выражений.
Во многих случаях интегрирование рациональной функции удается выполнить, сведя эту функцию к рациональной. Этот прием называют рационализацией подынтегральной функции, а подстановку – рационализирующей. Существо метода покажем на примерах
Пусть
![]() .
.
Полагая
![]() ,
находим
,
находим
![]() откуда
откуда
![]() .
.
Дело свелось к интегрированию рациональной дроби. Поскольку дробь неправильная, то делим с остатком числитель на знаменатель
![]()
Остается вернуться к старой переменной x, заменяя z
![]()
Аналогичным образом для интеграла
![]()
рационализирующая
подстановка имеет вид
![]() ,
ибо x
фигурирует у нас под корнем кубическим.
Выполняя эту подстановку, находим
,
ибо x
фигурирует у нас под корнем кубическим.
Выполняя эту подстановку, находим
![]()
откуда
![]()
Сложнее обстоит дело в случае интеграла
![]() .
.
Ведь
здесь x
фигурирует и под знаком квадратного и
под знаком кубического корня. Чтобы эти
оба корня извлеклись, естественно
положить
![]() .
Это дает
.
Это дает
![]()
откуда
![]()
После разбора этих примеров становится ясным следующее правило: если f (u, v,w,…) – рациональная функция своих аргументов, а a,b,… - целые положительные числа, то интеграл
![]() (1)
(1)
приводится к интеграл от рациональной функции при помощи подстановки
![]() ,
(2)
,
(2)
где N – наименьшее общее кратное показателей корней.
Сходная подстановка рационализирует подынтегральную функцию и в более общем интеграле
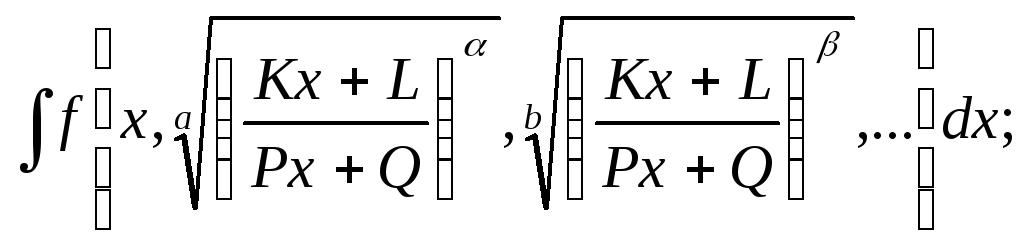 (3)
(3)
где f – рациональна, a,b,… - целые, а K, L, P, Q – постоянные.
Именно, здесь надо положить
![]() , (4)
, (4)
где N, как и выше, - наименьшее общее кратное показателей корней.
Рассмотрим следующий пример:
-
Пусть
![]()
Полагая
![]() находим
находим
![]()
значит
![]()
Рассмотрим теперь интегралы вида:
![]() (5)
(5)
Подобные интегралы вычисляются без труда в следующих случаях:
А) числитель Ax+B есть производная подкоренного трехчлена в знаменателе;
В) числитель не зависит от x, т.е. A=0.
Действительно, в случае
а) надо положить
![]() ,
что приводит интеграл (5) к виду
,
что приводит интеграл (5) к виду
![]()
Например,
![]()
В случае в) интеграл можно рационализовать с помощью подстановок Эйлера.
-
первая подстановка Эйлера применяется при a>0:
![]() ;
;
-
вторая подстановка Эйлера применяется в случае
 :
:
![]() ;
;
-
третья подстановка Эйлера применяется при c>0:
![]() .
.
В правой
части подстановок может быть выбрана
любая комбинация знаков; в конкретных
случаях надо выбирать конкретную
комбинацию.
![]()
Пример. Найти
![]() .
.
Решение. Применим первую подстановку Эйлера:
![]()
![]() Следовательно,
Следовательно,
![]()
Подстановки Эйлера, играя важную теоретическую роль, на практике приводят обычно к громоздким выкладкам, поэтому прибегать к ним надо в тех случаях, когда не удается вычислить интеграл ни одним из других способов.
2. Интегрирование выражений, содержащих тригонометрические функции.
В этом пункте мы докажем интегрируемость любой функции вида:
![]() ,
где R – рациональная
функция.
,
где R – рациональная
функция.
Докажем, что интеграл
от этой функции рационализируется
подстановкой
![]() .
Действительно,
.
Действительно,
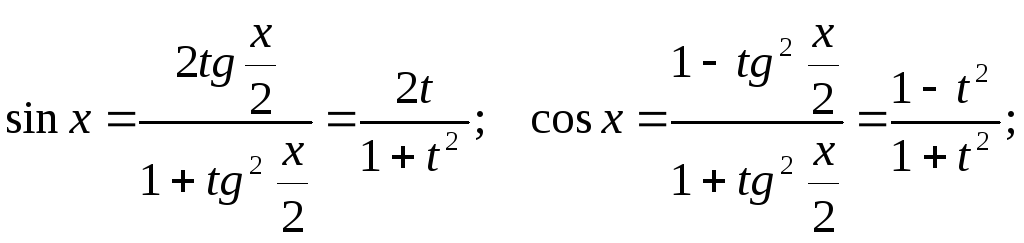
![]()
Отсюда получаем
![]() ,
,
т.е. мы получили интеграл от рациональной функции.
Пример. Вычислить
интеграл
![]()
Решение. Применяя универсальную тригонометрическую подстановку, получим
![]()
 .
.
Рассмотрим отдельно два случая:
-
0<a<1
![]()
-
a>1

На практике универсальная тригонометрическая подстановка часто приводит к громоздким выкладкам. В ряде случаев удобны другие подстановки:
a) t=cosx, если R(-sinx, cosx)=-R(sinx, cosx);
b) t=sinx, если R(sinx, -cosx)=-R(sinx, cosx);
c) t=tgx, если R(-sinx, -cosx)=-R(sinx, cosx).
Для практического получения выражений неопределенных интегралов в конечном виде составлены обширные справочники и таблицы. Однако, доказано, что существуют функции, первообразные которых, а значит и неопределенные интегралы, в элементарных функциях не выражаются. Эти неопределенные интегралы существуют, имеют важные практические приложения и подробно изучаются в математическом анализе. Укажем некоторые из них:
![]()
![]()
Отметим
еще интеграл
![]() где a, b –
произвольные постоянные, а m,
n, p –
рациональные числа, причем a,
b, n отличны
от нуля; подынтегральное выражение
такого вида называется биномиальным
дифференциалом. Великий русский математик
П. Л. Чебышев доказал, что этот интеграл
выражается в элементарных функциях в
том и только в том случае, когда хотя бы
одно из чисел
где a, b –
произвольные постоянные, а m,
n, p –
рациональные числа, причем a,
b, n отличны
от нуля; подынтегральное выражение
такого вида называется биномиальным
дифференциалом. Великий русский математик
П. Л. Чебышев доказал, что этот интеграл
выражается в элементарных функциях в
том и только в том случае, когда хотя бы
одно из чисел
![]() целое. Если же это условие не выполнено,
то указанный интеграл в элементарных
функциях не выражается.
целое. Если же это условие не выполнено,
то указанный интеграл в элементарных
функциях не выражается.
Контрольные вопросы по теме занятия:
-
Напомните определение первообразной.
-
Дайте определение неопределенного интеграла.
-
Вспомните таблицу интегралов, введенную в предыдущей лекции.
Контрольные вопросы по теме занятия:
-
Напомните определение первообразной.
-
Дайте определение неопределенного интеграла.
-
Вспомните таблицу интегралов, введенную в предыдущей лекции.
Заключение.
В лекции рассмотрены вопросы, посвященные методам интегрирования. В первом вопросе лекции рассмотрены алгоритмы интегрирования простейших иррациональных функций. Во втором вопросе лекции рассмотрены методы интегрирования тригонометрических функций. Приведены некоторые интегралы, не выражающиеся в элементарных функциях. К практическому занятию необходимо изучить вопросы, рассмотренные на лекции. Данная лекция и практическое занятие имеют свое продолжение в теме «Определенный интеграл», «Кратные интегралы» и др.
