билеты экзамен матан
.docxПервообразная и неопределенный интеграл. Основные свойства неопределенного интеграла.
Первообразная и неопределенный интеграл
Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции
F'(x) = f(x).
Обозначение
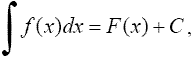
где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением. 2. Свойства неопределенного интеграла
1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
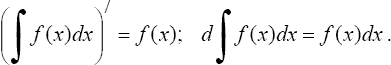
2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
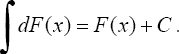
3. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то
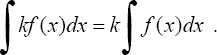
4
. Неопределенный интеграл от алгебраической
суммы двух функций равен алгебраической
сумме интегралов от этих функций в
отдельности.
2.
Таблица основных интегралов.

3. Основные методы интегрирования. Примеры.
Наиболее важными методами интегрирования являются: 1) метод непосредственного интегрирования (метод разложения),
Пример. ![]() 2)
метод подстановки (метод введения новой
переменной),
2)
метод подстановки (метод введения новой
переменной),
Пример.  3)
метод интегрирования по частям.
3)
метод интегрирования по частям.
Пример. Найти неопределенный интеграл ∫xe-2xdx
Воспользуемся
методом интегрирование по частям.
Положим u=x, dv=e-2xdx.
Тогда du=dx, v=∫xe-2xdx=-![]() e-2x+C
Следовательно
по формуле имеем:
∫xe-2xdx=x(-
e-2x+C
Следовательно
по формуле имеем:
∫xe-2xdx=x(-![]() e-2x)-∫-
e-2x)-∫-![]() -2dx=-
-2dx=-![]() e-2x-
e-2x-![]() e-2x+C
e-2x+C
4. Определенный интеграл. Площадь криволинейной трапеции. Формула Ньютона-Лейбница.
Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемаяфункция или функционал, а вторая — область в множестве задания этой функции (функционала)
Определённый
интеграл 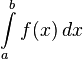 численно
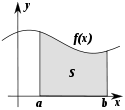
равен площади фигуры, ограниченной осью
абсцисс, прямыми
численно
равен площади фигуры, ограниченной осью
абсцисс, прямыми ![]() и
и ![]() и
графиком функции
и
графиком функции ![]() .
.
Если ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() и
и ![]() —
её любая первообразная на этом отрезке,
то имеет место равенство
—
её любая первообразная на этом отрезке,
то имеет место равенство
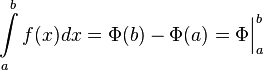
5. Основные свойства определенного интеграла. Формулы замены переменной и интегрирования по частям в определенном интеграле.
Сво-во :
Если
функция ![]() интегрируема
по Риману на
интегрируема
по Риману на ![]() ,
то она ограничена на нем
,
то она ограничена на нем
Формула
интегрирования по частям в определенном
интеграле выводится так же, как и для
неопределенного интеграла, и имеет
вид ![]()
6. Несобственные интегралы.
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
-
Предел a или b (или оба предела) являются бесконечными;
-
Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b]
7. Двойной интеграл.
В математическом анализе кратным или многократным интегралом называют множество интегралов, взятых от переменных. Например: Замечание: кратный интеграл − это определённый интеграл, при его вычислении всегда получается число
8. Обыкновенные дифференциальные уравнения (ОДУ). Основные определения. Задача Коши для уравнений первого и второго порядков.
Обыкнове́нные дифференциа́льные уравне́ния (ОДУ) — это дифференциальное уравнение вида
![]()
где ![]() —
неизвестная функция ,
зависящая от независимой переменной
—
неизвестная функция ,
зависящая от независимой переменной ![]() ,
штрих означает дифференцирование по
,
штрих означает дифференцирование по ![]() .
Число
.
Число ![]() называется порядком дифференциального
уравнения(1)
называется порядком дифференциального
уравнения(1)
Задача
Коши
(задача с начальным условием).
Пусть функция f(x, y) определена
в области D,
точка ![]() .
Требуется найти решение уравнения
.
Требуется найти решение уравнения
|
|
(8) |
удовлетворяющее начальному условию
|
|
(9) |
-
(начальное условие (9) часто записывают в форме
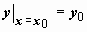 ).
).
 Теорема
Коши
(существования
и
решения
задачи
Коши).
Если
в
области D функция f(x, y) непрерывна
и
имеет
непрерывную
частную
производную
Теорема
Коши
(существования
и
решения
задачи
Коши).
Если
в
области D функция f(x, y) непрерывна
и
имеет
непрерывную
частную
производную  ,
то
для
любой
точки
,
то
для
любой
точки 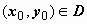 в
окрестности
точки x0 существует
единственное
решение
задачи
((8),(9)).
Мы
примем
эту
теорему
без
доказательства.
На
самом
деле
для
существования
решения
в
окрестности
точки x0 достаточно
только
непрерывности
функции
в
окрестности
точки x0 существует
единственное
решение
задачи
((8),(9)).
Мы
примем
эту
теорему
без
доказательства.
На
самом
деле
для
существования
решения
в
окрестности
точки x0 достаточно
только
непрерывности
функции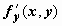 f(x, y);
условие
непрерывности обеспечивает
единственность
этого
решения. 6
f(x, y);
условие
непрерывности обеспечивает
единственность
этого
решения. 6 -
9. Основные виды ОДУ первого порядка. Методы решения.
-
Уравнения с разделяющимися переменными
-
Дифференциальное уравнение
 называется уравнением
с разделяющимися (отделяющимися)
переменными,
если его правая часть представима в
виде
называется уравнением
с разделяющимися (отделяющимися)
переменными,
если его правая часть представима в
виде  .
Тогда, в случае
.
Тогда, в случае 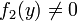 ,
общим решением уравнения является
,
общим решением уравнения является 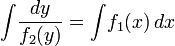 .
. -
-
Дифференциальное уравнение
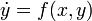 называется однородным,
если
называется однородным,
если 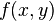 —
однородная функция нулевой степени.
Функция
—
однородная функция нулевой степени.
Функция  называется
однородной степени
называется
однородной степени 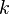 ,
если для любого
,
если для любого 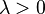 выполняется
равенство
выполняется
равенство 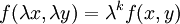 .
. -
Замена
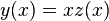 приводит
при
приводит
при 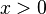 однородное
уравнение к уравнению с разделяющимися
переменными:
однородное
уравнение к уравнению с разделяющимися
переменными: -
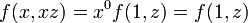
-

-
Подставив в исходное уравнение, получаем:
-
 ,
, -
что является уравнением с разделяющимися переменными.
-
-
Квазиоднородные уравнения
-
Дифференциальное уравнение
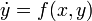 называется квазиоднородным,
если для любого
называется квазиоднородным,
если для любого 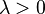 выполняется
соотношение
выполняется
соотношение 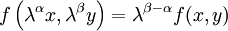 .
. -
Данное уравнение решается заменой
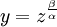 :
: -
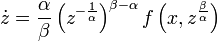
-
В силу квазиоднородности, положив
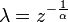 ,
получаем:
,
получаем: -

-
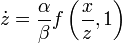 ,
, -
что, очевидно, является однородным уравнением.
-
-
Линейные уравнения[править | править исходный текст]
-
Основная статья: Линейное дифференциальное уравнение
-
Дифференциальное уравнение
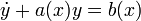 называется линейным и
может быть решено двумя методами:
методом интегрирующего множителя или
методом вариации постоянной.
называется линейным и
может быть решено двумя методами:
методом интегрирующего множителя или
методом вариации постоянной. -
Метод интегрирующего множителя[править | править исходный текст]
-
Пусть задана функция
 —
интегрирующий множитель, в виде:
—
интегрирующий множитель, в виде: -

-
Умножим обе части исходного уравнения на
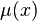 ,
получим:
,
получим: -
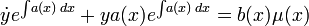
-
Легко заметить, что левая часть является производной функции
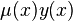 по
по 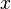 .
Поэтому уравнение можно переписать:
.
Поэтому уравнение можно переписать: -
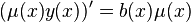
-
Проинтегрируем:
-
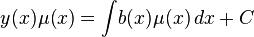
-
Таким образом, решение линейного уравнения будет:
-
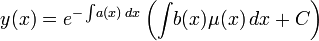
-
Метод вариации постоянной (метод Лагранжа)[править | править исходный текст]
-
Основная статья: Метод Лагранжа (дифференциальные уравнения)
-
Рассмотрим однородное уравнение
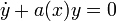 .
Очевидно, это уравнение с разделяющимися
переменными, его решение:
.
Очевидно, это уравнение с разделяющимися
переменными, его решение: -
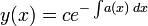
-
Решения исходного уравнения будем искать в виде:
-
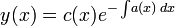
-
Подставив полученное решение в исходное уравнение:
-
 ,
, -
получаем:
-
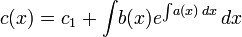 ,
, -
где
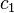 —
произвольная константа.
—
произвольная константа. -
Таким образом, решение исходного уравнения можно получить путем подстановки
 в
решение однородного уравнения:
в
решение однородного уравнения: -
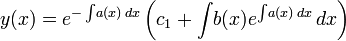
-
10. ОДУ высших порядков допускающие понижение порядка. Методы решения.
-
Если дифференциальное уравнение
-
F(x, y, y ',..., y(n) ) = 0
-
содержит производную неизвестной функции y = y(x) порядка n выше первого, то его называют уравнением n-го порядка и относят к уравнениям высших порядков.
-
Такое уравнение в нормальной форме имеет вид
-
y(n) = f (x, y, y ', ..., y(n - 1) ).
-
Пусть D область определения функции f (x, y, y ', ..., y(n - 1) ), D из Rn + 1 . Функция y = y(x) называется решением уравнения n–го порядка на отрезке [a; b] , если:
-
− при всех x ∈ [a; b] точка (x, y(x), y '(x) ,..., y(n −1) ) принадлежит области D;
-
− y = y(x) дифференцируема n раз на [a; b] и при всех x ∈ [a; b] выполняется тождество y(n)(x) ≡ f (x, y(x), y '(x), ..., y(n - 1) (x) ).
-
График решения y = y(x) называется интегральной кривой уравнения.
-
Для того, чтобы найти вполне определенную интегральную кривую, нужно задать дополнительные условия. Для уравнения n –го порядка таких условий должно быть n.
-
Начальной задачей или задачей Коши для уравнения n–го порядка
-
y(n) = f (x, y, y ', ..., y(n - 1) )
-
называется задача отыскания решения y = y(x), удовлетворяющего начальным условиям
-
y(x0) = y0, y '(x0) = y10, ..., y(n - 1) (x0) = y(n - 1)0 .
-
Здесь (x0, y0, y10, ..., y(n - 1)0 ) фиксированная точка области D.
-
Любое фиксированное решение y = φ(x) — решение некоторой задачи Коши — называется частным решением уравнения .
-
Общим решением уравнения n –го порядка называется функция y = φ(x,C1,..., Cn) , зависящая от n произвольных постоянных C1,..., Cn и удовлетворяющая следующим требованиям:
-
− при любых допустимых значениях постоянных C1,..., Cn функция y = φ(x,C1,..., Cn) является решением уравнения на [a;b] ;
-
− какова бы ни была начальная точка (x0, y0, y10, ..., y(n - 1)0 ) ∈ D , существуют такие значения постоянных значения C1*,..., Cn* такие, что функция y = φ(x,C1*,..., Cn*) удовлетворяет начальным условиям
-
φ(x0,C1*,..., Cn*) = y0 , φ '(x0,C1*,..., Cn*) = y10, ..., φ(n - 1)(x0,C1*,... , Cn*) = y(n - 1)0 .
-
Равенство Φ(x,C1,..., Cn) = 0 называется общим интегралом уравнения n –го порядка в области D , если оно неявно определяет общее решение уравнения .
-
-
Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ',..., y(n) ) = 0 может быть понижен, то говорят, что уравнениедопускает понижение порядка.
-
-
К уравнениям, допускающим понижение порядка, относятся в частности, уравнения, не содержащие искомой функции и ее производных до некоторого порядка, , т.е. уравнения вида
-
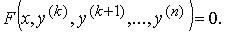
-
Заменой z(x) = y(k)(x) такое уравнение сводится к уравнению (n−k)–го порядка:
-

-
Если z = z(x,C1,...,Cn-k) решение этого уравнения, то общее решение уравнения n–го порядка может быть вычислено по формуле
-

-
Простейшее уравнение, допускающее понижение порядка — уравнение вида y(n) = f (x), его общее решение имеет вид
-