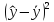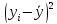отчет по эконометрике 1

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ»

(СПбГЭУ)

Отчет по лабораторной работе №1

«Эконометрика»

Выполнила:

Драганчук Марина

Группа М3421

Санкт-Петербург

2014

1. Статистическая совокупность данной лабораторной работы состоит из 50 элементов. Каждая единица совокупности является вином сорта Каберне Совиньон. Статистическая совокупность была проанализирована по ряду качественных и количественных признаков (характеристик): «выдержка», «содержание винограда сорта Каберне Совиньон», «цена», «объем», «крепость».

Таблица №1 - «Вина сорта Каберне Совиньон»

Продолжение таблицы №1

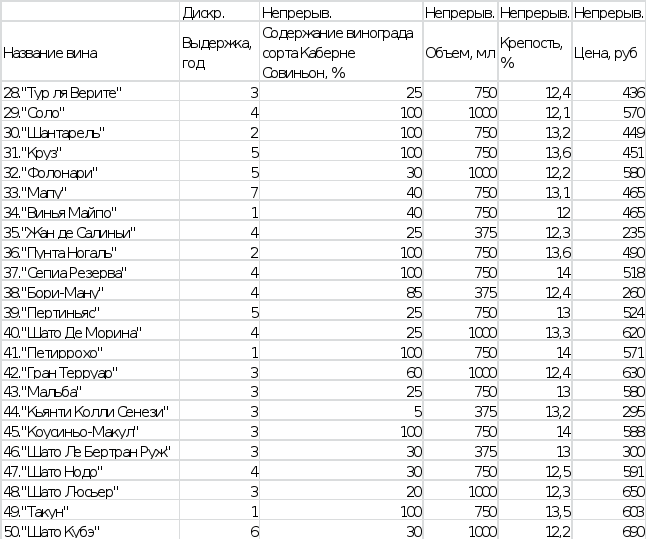
Источник данных - сайт winestyle.ru.

Для построения аналитической группировки был выделен признак-фактор и признак-результат. В качестве признака-фактора (x) я выбрала признак «крепость», а признак-результат (y) – «цена». Далее была произведена группировка единиц совокупности по признаку-фактору (х). По каждой полученной группе были отобраны соответствующие значения признака-результата (y) и на их основе рассчитан некоторый обобщающий показатель – среднее значение y.

Таблица №2 – «Аналитическая группировка»

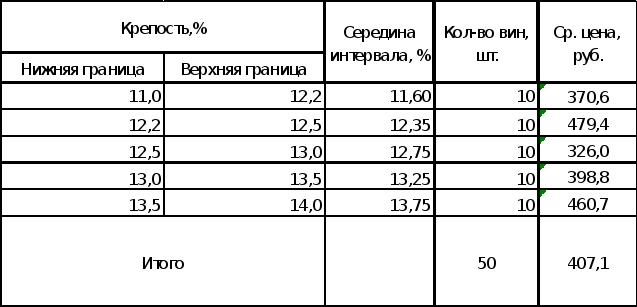
2. Далее я рассчитала общую дисперсию, используя свойство разложения дисперсий. Общая дисперсия характеризует вариацию признака, как результат влияния всех факторов. 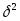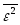По теореме о разложении дисперсии общая дисперсия признака-результата (цена) может быть разложена на составляющие: межгрупповую, (характеризует часть вариации, обусловленную влиянием фактора, положенного в основу группировки) среднюю из внутригрупповых дисперсий, (характеризует часть вариации, происходящую под влиянием прочих факторов):

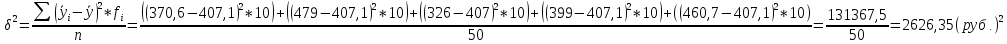
Сравнив дисперсию, полученную по теореме о разложении дисперсий и ту, что получила в Excel’е, я получила одинаковые значения, что говорит о том, что расчет произведен верно.

3. Далее рассчитываем эмпирическое корреляционное отношение. Оно рассчитывается, как корень из эмпирического коэффициента детерминации.

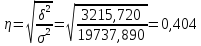, связь слабая.

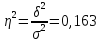, доля вариации признака y «цена» под влиянием признака х «крепость».

Для того, чтобы рассчитать коэффициент линейной парной корреляции, для начала рассчитаем ковариацию- cov(x,y) – показатель совместной вариации признаков:

Таблица №3 – «Показатели для расчета коэффициента линейной парной корреляции»

Крепость,% (x)	Цена, руб (y)	x*y
11	120	1320
11	360	3960
11,2	364	4076,8
11,5	201	2311,5
12	311	3732
12	390	4680
12,1	570	6897
12,1	465	5626,5
12,2	235	2867
12,2	690	8418
12,3	650	7995
12,4	591	7328,4
12,4	630	7812
12,4	260	3224
12,4	580	7192
12,4	436	5406,4
12,4	418	5183,2
12,5	415	5187,5
12,5	408	5100
12,5	406	5075
12,6	405	5103
12,7	390	4953
12,7	182	2311,4
12,7	344	4368,8

Продолжение таблицы №3

Крепость,% (x)	Цена, руб (y)	x*y
12,8	155	1984
12,8	220	2816
13	333	4329
13	380	4940
13	402	5226
13	449	5837
13,1	465	6091,5
13,2	524	6916,8
13,2	620	8184
13,2	580	7656
13,2	295	3894
13,3	300	3990
13,3	176	2340,8
13,4	307	4113,8
13,4	333	4462,2
13,5	388	5238
13,6	191	2597,6
13,6	451	6133,6
13,6	490	6664
13,6	603	8200,8
14	380	5320
14	397	5558
14	418	5852
14	518	7252
14	571	7994
14	588	8232
Среднее значение
12,82	407,1	5239,032

cov(x,y)= 5239,032-12,82*407,1=20,01 (руб.*%)

Далее рассчитываем коэффициент линейной парной корреляции по формуле Пирсона:

(%)

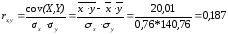
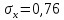(руб.)

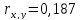, связь прямая линейная, связь между данными факторами практически отсутствует.

4. Далее рассчитываем величину 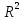- коэффициент детерминации. Он определяет долю вариации одной из переменных, которая объясняется вариацией другой переменной (по конкретному уравнению регрессии).

=>3,5%

Это значит, что 3,5% общей вариации цены обусловлено влиянием крепости (по линейному уравнению регрессии).

=

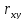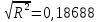
По данному значению коэффициента можно судить, что между признаками «крепость» (x) и «цена» (у) существует слабая связь.

Таблица №4- «Показатели для расчета коэффициента детерминации»

3931,7	82426,41
3931,7	2218,41
3931,7	1857,61
3115,1	42477,21
2068,2	9235,21
798,1	292,41
798,1	26536,41
615,3	3352,41
615,3	29618,41
456,3	80032,41
456,3	59000,41
321,0	33819,21
209,4	49684,41
209,4	21638,41
209,4	29894,41
209,4	835,21
209,4	118,81
209,4	62,41
121,5	0,81
121,5	1,21
121,5	4,41
57,4	292,41
17,1	50670,01
17,1	3981,61

Продолжение таблицы №4

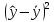
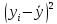17,1

63554,4

0,5

35006,4

0,5

5490,8

38,5

734,4

38,5

26,0

38,5

1755,6

38,5

3352,4

93,1

13665,6

171,4

45326,4

171,4

29894,4

171,4

12566,4

171,4

11470,4

273,5

53407,2

273,5

10020,0

399,3

5490,8

399,3

364,8

548,9

46699,2

722,2

1927,2

722,2

6872,4

722,2

38376,8

722,2

734,4

1652,7

102,0

1652,7

118,8

1652,7

12298,8

1652,7

26863,2

1652,7

32724,8

36748,7

986894,5

5. Далее рассчитываем параметры а и b и составляем уравнения.

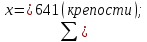
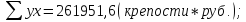
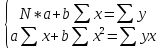
Подставим наши данные в систему:

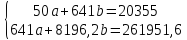
Рассчитаем значения параметров a и b по следующим формулам:

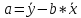
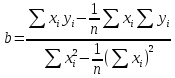
Подставим наши значения:

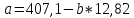
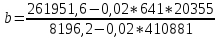
Из первого уравнения выражаем а и подставим во второе уравнение:

Получаем эмпирические коэффициенты регрессии:

a = -34,58 (руб.)

b = 34,45 (руб./% крепости)

Линейное уравнение регрессии имеет вид

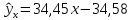
Коэффициент b=34,45 показывает, что при увеличении крепости вина на 1 %, его цена увеличивается в среднем на 34,45 руб.

Коэффициент «a» показывает значение цены при x=0(крепость= %), однако, данное значение невозможно в данной работе, так как в статистической совокупности не рассматриваются вина с нулевой крепостью,%