5. Теория экстремальных задач

Теория экстремальных задач изучает проблемы, связанные с экстремумом функционала в различных функциональных пространствах. Частью этой теории являются: вариационное исчисление, выпуклое программирование, динамическое программирование, дискретное программирование, квадратичное программирование, линейное программирование, математическое программирование, математическая теория оптимальных процессов, целочисленное программирование. Особое место в ней занимают задачи со многими критериями.

Экстремум – термин, объединяющий понятия максимума и минимума функции (функционала). Различают глобальный экстремум функции на множестве , т.е. частное значение функции, удовлетворяющие соотношениюдля всех(глобальный минимум) илидля всех(глобальный максимум), и локальный экстремум. В последнем случае неравенства выполняются в некоторой окрестноститочки экстремума. Глобальный экстремум функции называют также оптимумом функции или оптимальным значением функционала. Соответственно экстремальные задачи называют задачами оптимизации. В более общем случае речь идет об отыскании,на множестве(используется также символика,,,). Множествоназывают допустимым множеством экстремальной задачи, а- критерием экстремальной задачи (целевой функцией (функционалом) экстремальной задачи). Так как при изменении знака критерия имеем, то можно вести изложение только для случая минимизации критерия. Если существует вектортакой, что, т.е., тоназывают (глобальным) минимумом функционала (функции), т.е., а- точкой глобального минимума.

В теории экстремальных задач представляют интерес:

• существование глобального экстремума;

• необходимые и достаточные условия существовании я глобального экстремума для различных задач;

• методы поиска глобального экстремума;

• алгоритмы численного решения экстремальных задач.

Однако основные результаты теории экстремальных задач можно получить обычно только для локальных экстремумов. Если целевая функция (функционал) обладает рядом специфических свойств (например, она выпукла вниз на выпуклом множестве), то ее локальный минимум является глобальным. В общем случае это, к сожалению, не так.

Проблему существования решения иллюстрирует следующая задача оптимального управления: ,,,,. Минимальные значения критерию дает функция, не принадлежащая классу допустимых. Разбив отрезокначастейс допустимым управлением,, далее чередуя значенияна интервалах длины, и

получают в качестве ломанную такую, что

.

При интервал стремится к нулю, т.е. построенная последовательность допустимых решений,- минимизирующая. В задаче отыскания глобального экстремума непрерывной функции конечного числа переменных,(- замкнутое ограниченное пространство) существование (глобального) минимума (и глобального максимума)на этом множествегарантируется теоремой Вейерштрасса.

Под задачей поиска экстремума (минимума) функции (функционала) понимают:

1. нахождение самого экстремума ;

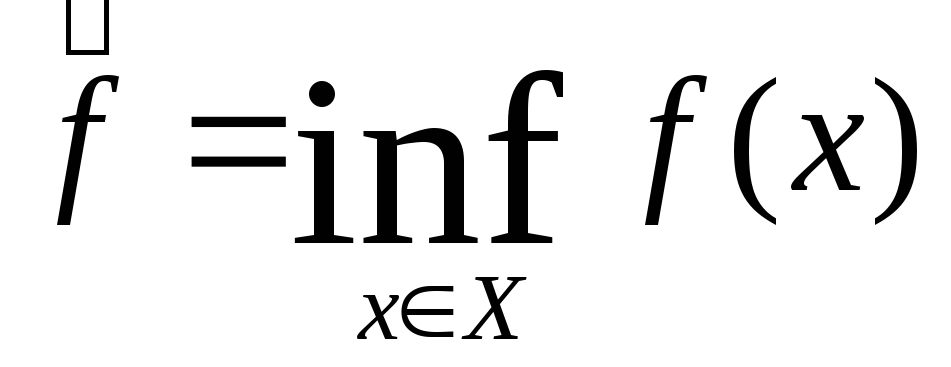2. нахождение точки минимума 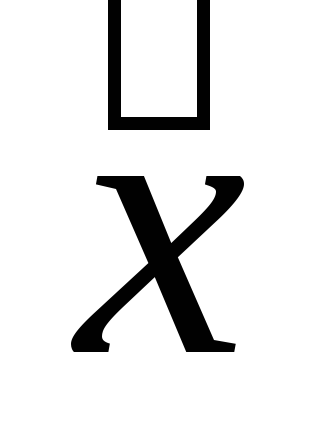, если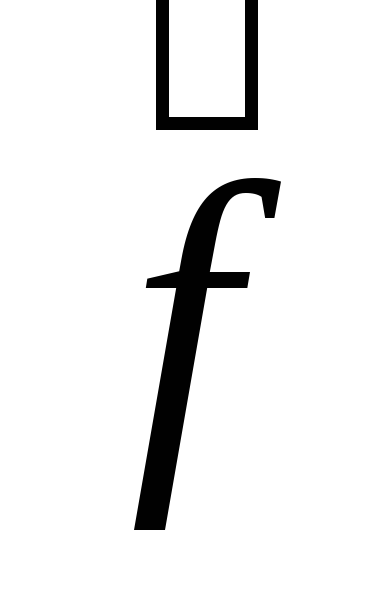достигается на допустимом множеств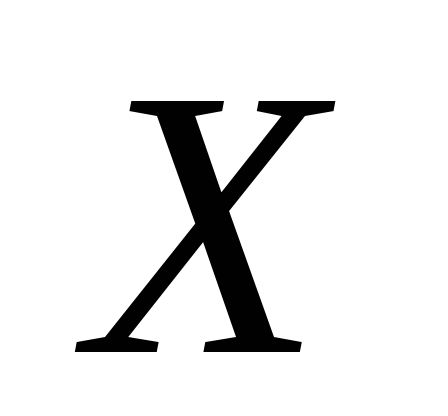е, т.е.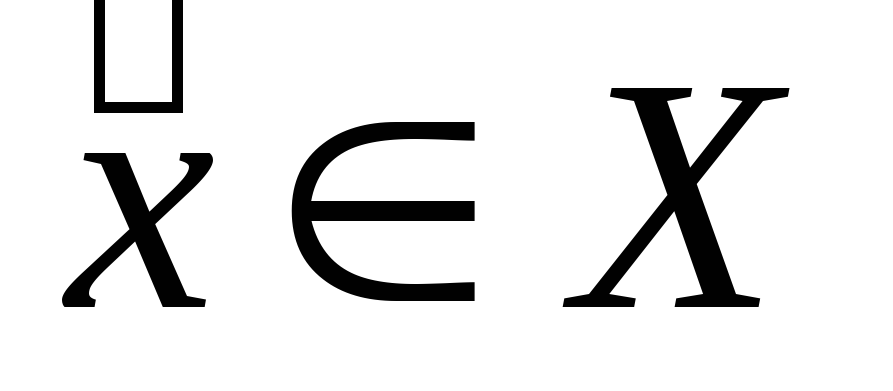,,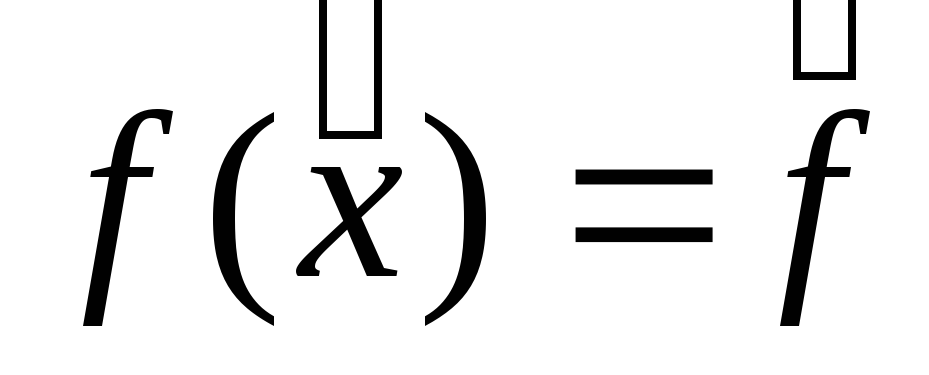 или минимизирующей последовательности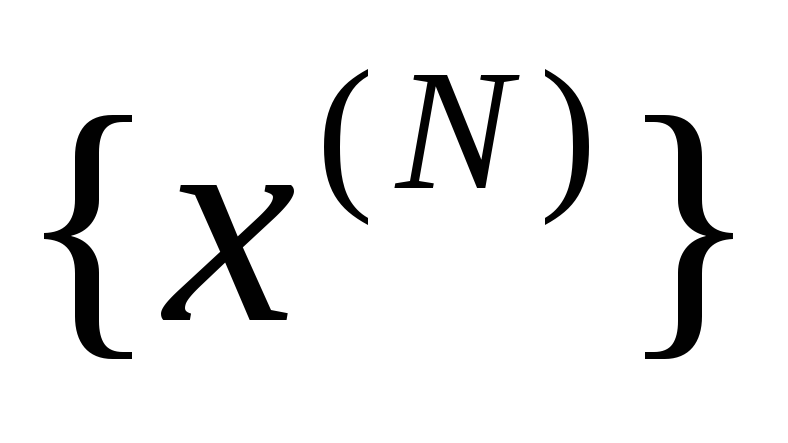, такой, что.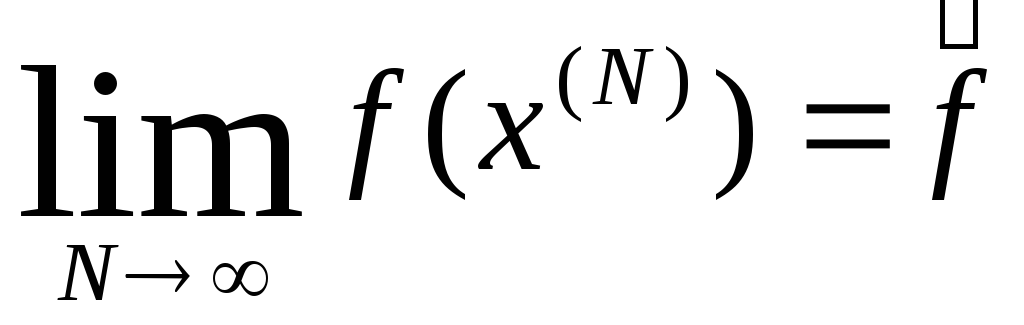

Ниже рассматриваются только экстремальные задачи для гладких функций векторного аргумента .

Если , т.е. ограничения на аргументотсутствуют, то говорят о задаче без ограничений отыскания экстремума функции, если же, то имеют дело с задачей с ограничениями.

Задачи с ограничениями сводятся к задаче без ограничений следующими приемами. Когда множество задано ограничениями типа равенств и неравенств, то, используя фигурирующие в них функции, нетрудно строить «штрафы»такие, что имеет место

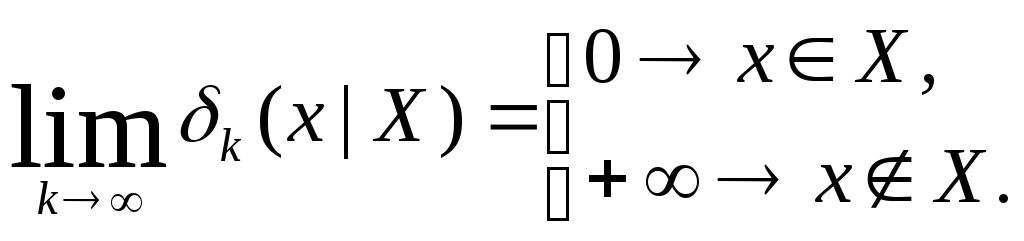
Тогда задача эквивалентна задаче. Если последовательностьпостроена так, что операции минимума и предела перестановочны, то получается последовательность задач без ограничений, т.е. задач безусловной минимизации, пределом решений которыхприбудет точкаминимума функциина множестве. Функцииназываются штрафными функциями. Различают внутренние (барьерные) и внешние штрафные функции. Барьерная функция неограниченно возрастает при приближениик границе. Например, в задаче

(1.4.1.)

барьерная функция вида , где число, называемое параметром штрафа, неограниченно растет с ростом. Внешняя штрафная функция обычно строится так, что штраф равен нулю на допустимом множествеи возрастает при удалении от него. Например, функция вида, где. Одним из недостатков численных методов отыскания экстремума, использующих штрафные функции, является потеря точности при перемножении больших величинна близкие к нулю для существенных ограничений величины. Поэтому применяют модифицированные штрафные функции со сдвигом значений

,

где ,,и выбираются при построении последовательностипропорционально невязке в выполнении ограничений. В этом случае к увеличениюприходится прибегать крайне редко (когда сумма невязок ограничений не уменьшается). Последнее утверждение следует из того, что примодифицированная функция штрафа переходит в функцию Лагранжа задачи с ограничениями. В частности, для задачи (1.4.1.) в, где множители,, носят название множителей Лагранжа. Так как

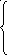, если все условия ,, выполнены,

, если хотя бы одно из них нарушено,

то задача (1.4.1.) эквивалентна задаче 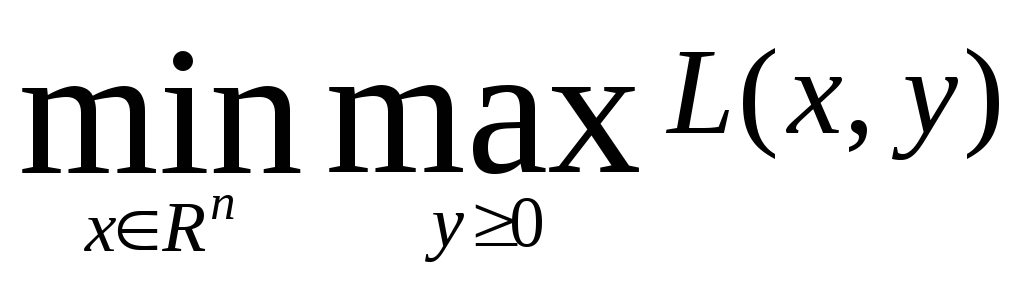. Задачуназывают двойственной по отношению к исходной (прямой) задаче (1.4.1.). Двойственные задачи играют большую роль в теории экономического равновесия. В случае, когда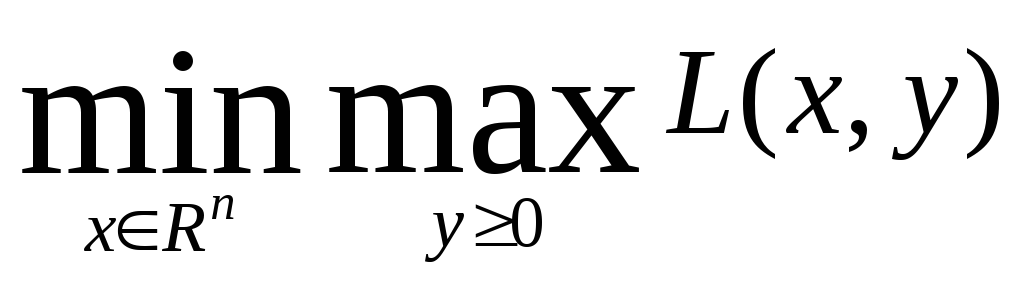=, говорят, что функцияимеет седловую точку. Пару () называют седловой точкой функции, если имеют место неравенства

(1.4.2.)

(в общем случае только для ),, лежащих в некоторой окрестности ()).

Необходимые условия экстремума обычно связывают для задачи (1.4.1.) с седловыми точками ее функции Лагранжа. Необходимые условия минимума для задачи (1.4.1.) следуют из неравенств (1.4.2.) при использовано разложения Тейлора

,

:

, (1.4.3.)

, ,(1.4.4.)

В экономической трактовке это означает наличие в точке минимума штрафных расценок,, отличных от нуля только для существенных ограничений, где, (второе условие (1.4.4.)) таких. Что малое дополнительное снижение ущерба при изменении любой компоненты, приводящее к нарушению ограничений задачи(1.4.1.), вызывает компенсирующий это снижение штраф (условие (1.4.3.)). В случае задач без ограниченийи (1.4.3.) переходит в известное необходимое условие экстремума функции,. Точки, удовлетворяющие необходимым условиям экстремума (как локально, так и глобально) называются стационарными.

Достаточные условия оптимальности получают заменой критерия некоторым выражением, оценивающим его снизу (в задаче на минимум), таким, что

1. ;

2. ;

3. 

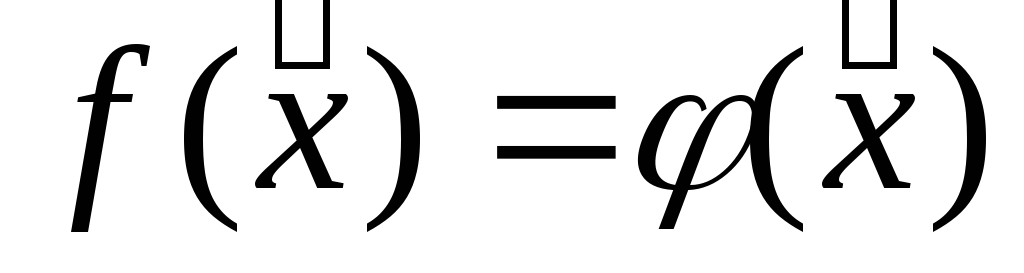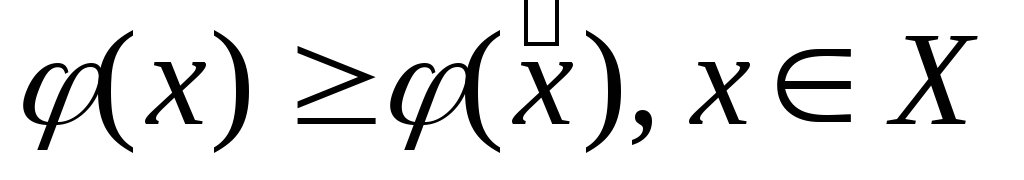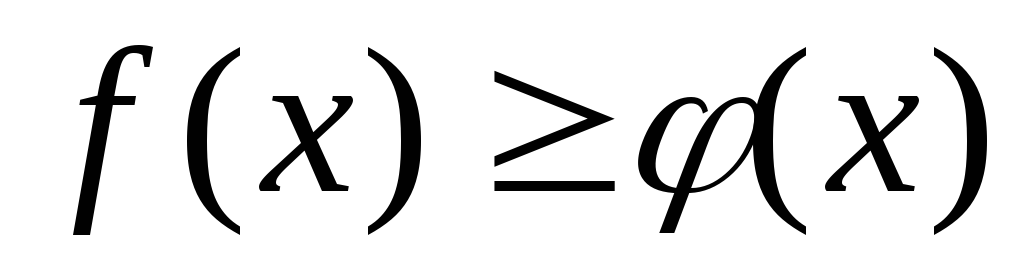
в области определения и релаксацией (ослаблением) ограничений задачи (расширением). В частности, для задачи на экстремум (как локальный, так и глобальный) функции,, оценивая ее квадратичной формой по формуле Тейлора, получаем известное условие положительной определенности матрицы вторых производныхв стационарной точке.

Классические (непрямые) методы поиска экстремума используют необходимые условия экстремума. Нули частных производных , вычисляются одним из многочисленных методов последовательных приближений. С другой стороны, каждую задачу решения системы уравнений,,, можно свести к задаче поиска экстремума (минимума), например, функции. Прямые методы поиска основаны на непосредственном сравнениив двух или нескольких точках и итеративных пересчетах прямых и сопряженных переменных (множителей Лагранжа). Так как задача на экстремум с ограничениями сводится к задаче без ограничений, то ниже излагаются алгоритмы поиска экстремума задачи без ограничений. Применяют алгоритмы построения последовательности значений, использующие линейное приближение минимизируемой функции, например, метод градиентного спуска

,

использующий квадратичное приближение, метод Ньютона

,

где - единичная матрица (метод градиентного спуска и метод Ньютона получаются приилисоответственно).

Методы поиска экстремума, использующие первую производную, называют методами первого порядка, а использующие вторую – методами второго порядка. Параметры ,выбираются так, чтобыдля всех(условие релаксации). В некоторых предположениях доказывается сходимость алгоритмов, чаще всего в смыслеили.

Если имеет место неравенство , то приговорят, что имеет место сверхлинейная сходимость, а при- квадратичная сходимость. В достаточно широких предположениях метод Ньютона и его модификации имеют квадратичную сходимость. Существуют методы первого порядка, не использующие вторых производных с квадратичной сходимостью, например, разностные аппроксимации метода Ньютона и другие квазиньютоновские методы сопряженных градиентов.

Для овражных функций, рельеф которых имеет форму «оврагов» с крутыми склонами (такой рельеф часто наблюдается у штрафных функций), разработаны специальные методы минимизации. Здесь предполагается после локального спуска из некоторых двух точек выполнять ускоряющий шаг в направлении, задаваемом двумя полученными на дне «оврага» точками. Для поиска минимума овражных функций применяют также метод тяжелого шарика другие методы, учитывающие инерцию при построении последовательности.