Тема 10. Моделирование транспортной деятельности

Задание 21. Система массового обслуживания и марковские цепи

Марковская цепь с дискретным состоянием и непрерывным временем характеризуется графом состояний (рисунок 2).

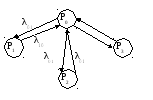
Рисунок 1 – Пример графа состояний

Для транспортного узла установить, что погрузо-разгрузочный механизм (ПРМ) на терминале может находиться в четырех состояниях: Р₀ – ПРМ работает; Р₁ – ПРМ простаивает в обслуживании; Р₂ – ПРМ не работает из-за организационных причин; Р₃ – ПРМ не работает в выходные и праздничные дни.

В течение месяца (30 дней) ПРМ находился в обслуживании в среднем 1 день через каждые 10 дней, простаивал по организационным причинам 1 день через каждые 12 дней. Также предусмотрено 2 выходных через каждые 15 дней. Определить вероятность нахождения ПРМ в каждом состоянии.

Пусть система характеризуется n состояниями S₀, S₁, S₂, …, S_n. Обозначим через P_i(k) вероятность того, что в момент времени t система S будет находиться в состоянии S_i (i = ). Требуется определить для любогоt вероятность состояний P₀(t), P₁(t), …, P_n(t). При этом следует учесть, что .

Вероятности состояний P_i(t) находят путем решения системы дифференциальных уравнений (уравнений Колмогорова), для i-го состояния имеющих вид:

.

Величина называется потоком вероятности перехода из состоянияS_i в S_j, причем интенсивность потоков может зависеть от времени или быть постоянной.

Интенсивность перехода потоков событий определяется:

1) если λ_ij зависит от интенсивности работы, то учитывается плотность распределения наработки до отказа;

2) если λ_ij зависит от количества дней, то – значение определяется как обратная функция к продолжительности периода.

При длительном протекании процесса говорят о предельном состоянии системы, которое не зависит от того, в каком состоянии система S была в начальный момент времени. Говорят, что в системе устанавливается стационарный режим, когда система переходит из состояния в состояние, но вероятности уже не меняется. В этом случае финальные вероятности получаются путем решения системы алгебраических уравнений, которые получаются из дифференциальных уравнений Колмагорова, если приравнять производные к нулю. Для нахождения значений P₁, P₂, …, P_n необходимо задать нормировочное условие .

Система массового обслуживания характеризуется следующими параметрами, которые определяются по формулам:

- параметр потока обслуживания:

,

где t – среднее время обслуживания, ч.;

- приведённая интенсивность потока:

,

где λ – средняя интенсивность поступления, ед./ч;

- вероятности состояний системы:

,

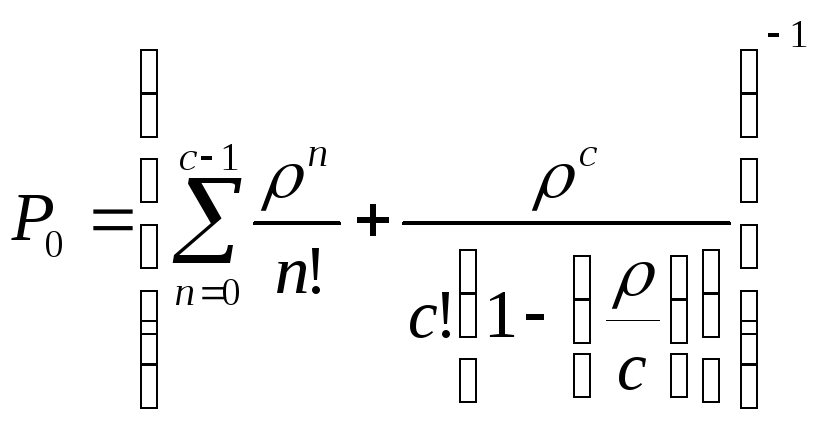где n – канал обслуживания, 0 ≤ n ≤ с;

c – количество каналов.

.

Применить указанный подход к транспортному узлу, который состоит из трёх постов, где осуществляется обработка контейнеров. Поток контейнеров (λ) составляет 2 единицы в час. Средняя продолжительность обслуживания – 1,5 часа. Определить параметры потока обслуживания, приведённую интенсивность потока заявок, а также предельную вероятность состояния системы. Предельная вероятность показывает вероятность отказа в обслуживании.