3. Первая и вторая задачи динамики.

Первая (прямая) задача.

Зная закон движения и массу точки, определить силу, действующую на точку.

Для решения этой задачи необходимо знать ускорение точ­ки.

1. Пусть движение точки задано в декартовых координатах

, ,

Определяем проекции ускорения на оси координат

,

а затем - проекции силы на эти оси:

.

Модуль и направление силы определяется по формулам

2. Если точка совершает криволинейное движение и извес­тен закон движения , траектория точки и ее радиус кри­визны, то удобно пользоваться естественными осями, а про­екции ускорения на эти оси определяются по фор­мулам:

на касательную ось

—касательное ускорение,

на нормаль

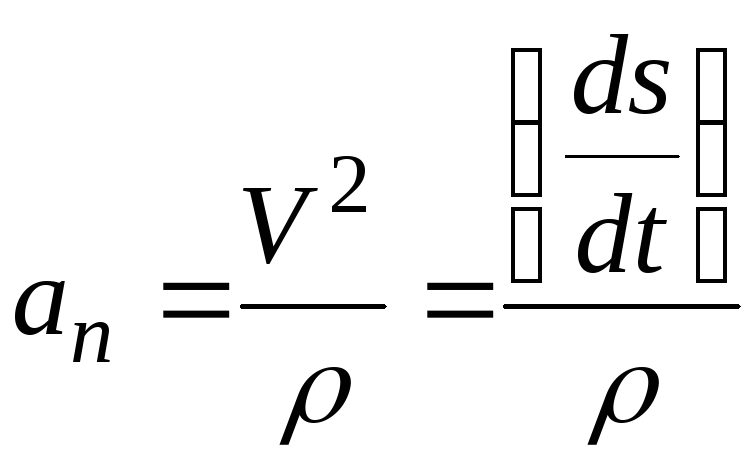— нормальное ускорение.

Проекция ускорения на бинормаль равна нулю. Тогда проекции силы на естественные оси

.

Модуль и направление силы определяется по формулам:

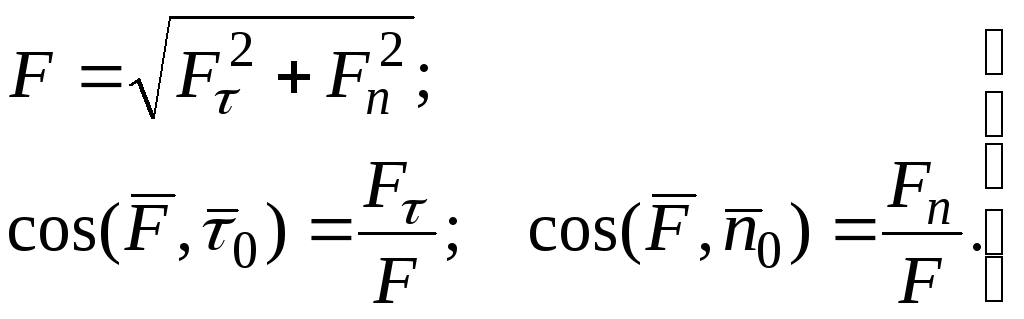
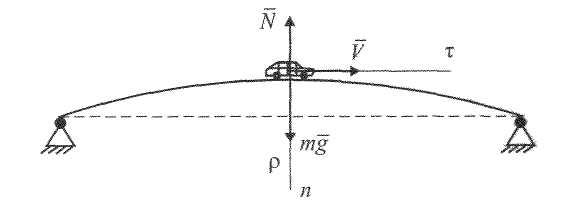
Задача 1. Автомобиль массы т = 1000 кг движется по выпуклому мосту со скоростью V = 20 м/с. Радиус кривизны в середине моста = 100м. Определить силу давления автомобиля на мост в момент, когда он находится на середине моста.

Решение. Считая автомобиль материальной точкой, изобразим его в середине моста и покажем силы: вес и нормаль­ную реакцию.

Второй закон динамики в векторной форме

.

Спроецируем это равенство на естественные оси и:

,

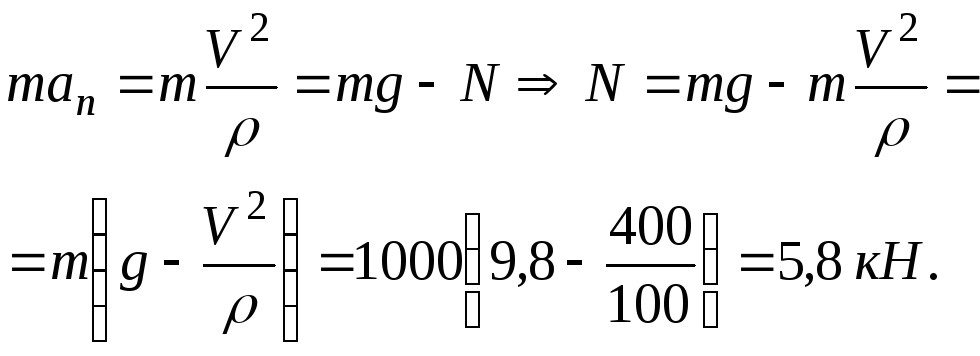
Задача 2. В кабине лифта, движущегося вверх рав­ноускоренно без начальной скорости, стоит человек массы т. Определить давление че­ловека на пол кабины, если за время t ка­бина поднялась на высоту h.

Решение. Объект движения — человек. Ось Ох направим в сторону движения. На человека действует реакция пола и его вес.

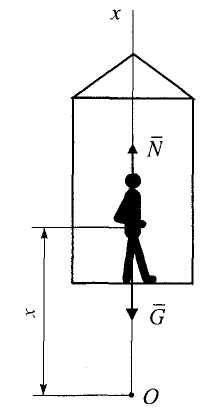
Запишем второй закон динамики в век­торной форме и затем в проекции на ось х:

.

Проекция ускорения на ось х

/

Реакция пола

.

Давление человека на пол равно реакции N и направлено в противоположную сторону.

При движении лифта вниз ось х на­правляется также вниз. Тогда

,

т. е. давление в этом случае меньше силы тяжести.

Вторая (обратная) задача.

Зная действующие на точку силы, ее массу и начальные условия движения, требуется определить закон ее движения .

Начальные условия движения точки в декартовых осях — это координаты точки и проекции начальной скоростина эти осив момент време­ни, соответствующий началу движения точки и принимаемый обычно равным нулю.

Вторую задачу динамики материальной точки рекомендуется решать в следующем порядке.

1. Составление расчетной схемы:

-изображение на рисунке в текущем положении точки (тела), действующих на нее сил и сил реакций связей;

-проведение координатных осей.

2. Выявление начальных условий движения точки.

3.Составление дифференциальных уравнений движения материальной точки:

.

4. Интегрирование дифференциальных уравнений движения.

5. Определение постоянных интегрирования.

6.Нахождение искомых величин и анализ полученных результатов.

Задача 3. По дороге на подъем двигается автомобиль с начальной скоростью . Угол подъема равен, коэффициент трения сколь­жения —f. Определить:

а) закон изменения скорости движения;

б) закон движения автомобиля;

в) время до остановки;

г) расстояние, пройденное до остановки.

Решение. 1.Составление расчетной схемы.

Изобразим автомобиль в произвольном положении на оси х, покажем силы, действующие на него: вес , силу тренияи нормальную реакциюдороги .

Выберем начало координат в начальном положении, ось х направим в сторону движения автомобиля.

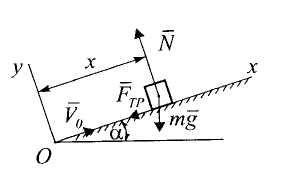
2.Определение начальных условий.

При t = 0, .

3. Запишем дифференциальное уравнение движения автомобиля по оси х

.

Получим

.

4. Проинтегрируем дважды это уравнение:

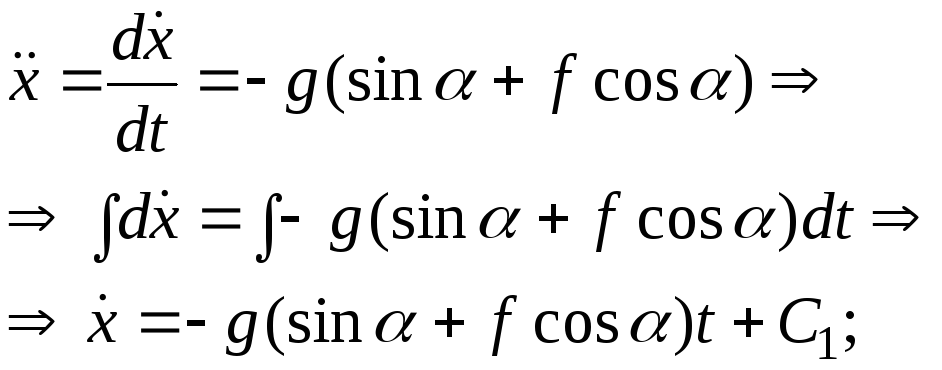
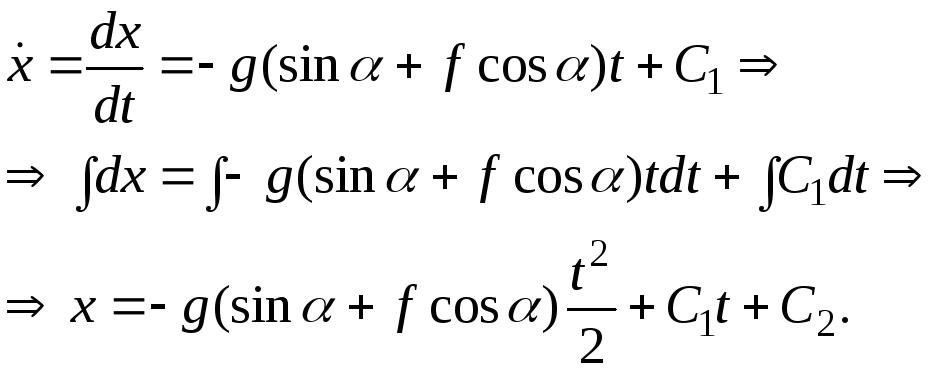
5. Найдем постоянные интегрирования с учетом начальных условий движения: при t = 0, .

Тогда

.

.

6. Закон изменения скорости

.

Закон движения

.

Время до остановки определим из условия V = 0 при t = Т.

.

Пройденное расстояние до остановки

.

Задача 4 . Автомобиль массы m движется горизонтально, сила сопро­тивления . В начальный момент автомобилю сообщили начальную скорость. Определить при:

а) закон изменения скорости движения;

б) закон движения автомобиля;

в) время движения, за которое скорость уменьшилась в 2 раза;

г) пройденное за это время расстояние.

Решение. 1. Составим расчетную схему.

Покажем в произвольном положении автомобиля силы, действующие на него: вес , силу сопротивления, нормальную реакцию.

Выберем начало координат в на­чальном положении автомобиля, ось х направим в сторону движения.

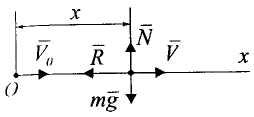
2. Запишем дифференциальное уравнение движения автомобиля вдоль оси х

так как .

3.Обозначим

.

Тогда

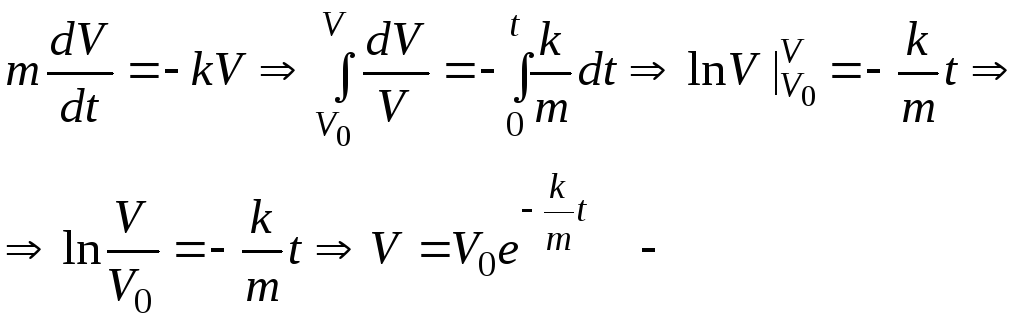
закон изменения скорости.

Представим

.

Разделим переменные и проинтегрируем:

.

(взят неопределенный интеграл).

4.Постоянную интегрирования С найдем с учетом начальных условий движения: при t = 0,

.

(.)

Закон движения

.

Время Т при

.

(. )

Пройденное за это время расстояние

( ).
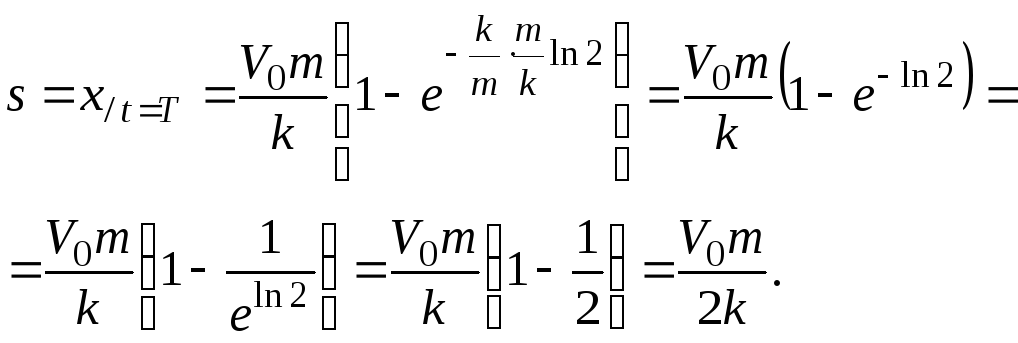