Лабораторная работа №10

Тема: Приложения производной и дифференциала

Теоретическая часть

1. Геометрический смысл производной.

2. Физический смысл производной.

3. Уравнения касательной и нормали к кривой. Угол между кривыми.

4. Наибольшее и наименьшее значения функции.

5. Геометрический смысл дифференциала.

6. Приближенное вычисление с помощью дифференциала.

7. Оценка погрешности (абсолютная и относительная).

Практическая часть

1-3. Написать уравнения касательной и нормали в заданной точке /2, стр. 126/.

1.1. №80 (а). 1.2. №83 (а). 1.3. №85 (б).

1.4. №86 (а). 1.5. №83 (б). 1.6. №86 (б).

2.1. №81(б). 2.2. №82 (б). 2.3. №89 (а).

2.4. №81 (в). 2.5. №82 (в). 2.6. №89 (в).

3.1. №84. 3.2. №87. 3.3. №88.

3.4. №84. 3.5. №87. 3.6. №88.

4. Найти угол между кривыми /2, стр. 126/.

4.1. №90. 4.2. №91. 4.3. №93. 4.4. №94. 4.5. №95. 4.6. №103.

5. Найти наибольшее и наименьшее значения функции на /2, стр.128/.

5.1. №109.I (а). 5.2. №109.I (б). 5.3. №109.I (в).

5.4. №109.II (а). 5.5. №109.II (б). 5.6. №109.II (в).

6. Вычислить приближенно с помощью дифференциала

6.1. . 6.2.. 6.3..

6.4. . 6.5.. 6.6..

Лабораторная работа №11

Тема: Производные и дифференциалы высших порядков. Формула Лейбница

Теоретическая часть

1. Производная и дифференциал второго порядка

а) обратной функции;

б) функции, заданной неявно;

в) функции, заданной параметрически.

2. Формулы производных 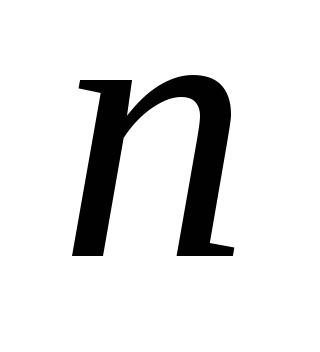-го порядка основных элементарных функций:

а) ;

б) ;

в) ;

г) ;

д) .

3. Формула Лейбница 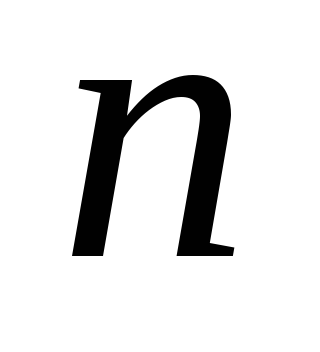-ой производной произведения двух функций.

Практическая часть

1. Найти и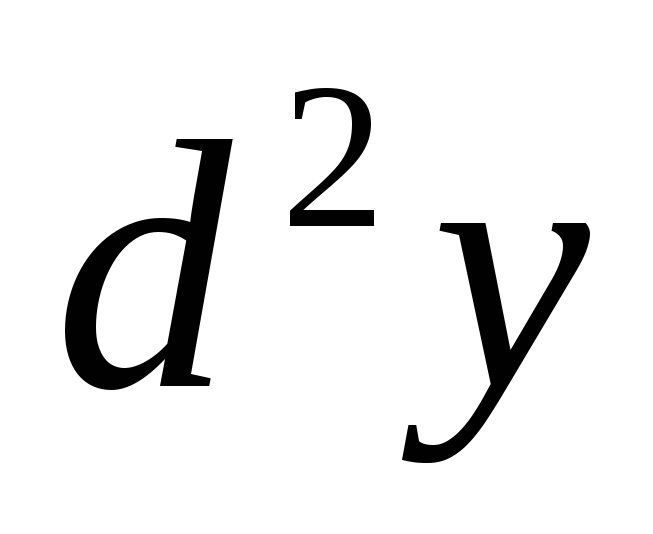функции, заданной неявно /2, стр. 125/.

1.1. № 63. 1.2. №64. 1.3. №65. 1.4. №66. 1.5. №67. 1.6. №68.

2. Найти и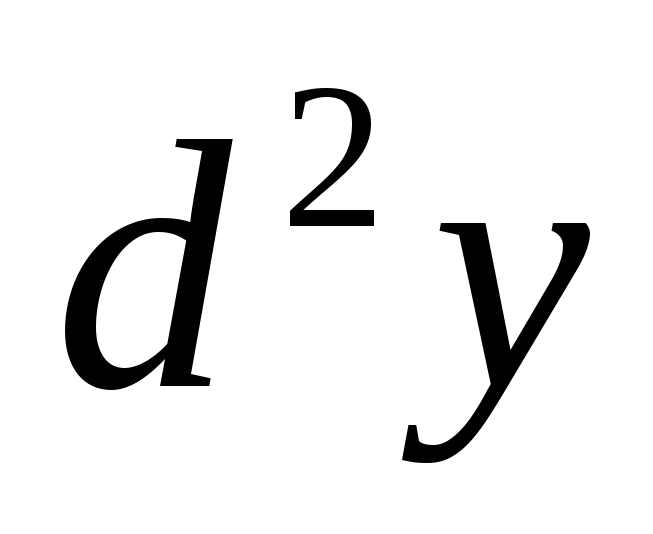функции, заданной параметрически /3/.

2.1. №1140. 2.2. №1141. 2.3. №1142.

2.4. №1143. 2.5. №1144. 2.6. №1142.

3. Найти производную 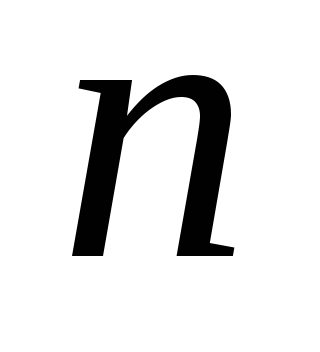-го порядка функции

3.1. . 3.2.. 3.3..

3.4. . 3.5.. 3.6..

4. Найти производную -го порядка функции по формуле Лейбница

/2, стр. 124-125/.

4.1. № 46. 4.2. №47. 4.3. №50. 4.4. №51. 4.5. №49. 4.6. №54.

5. Найти функции, считаяпромежуточным аргументом,

5.1. . 5.2.. 5.3..

5.4. . 5.5.. 5.6..

Лабораторная работа №12

Тема: Исследование функций и построение их графиков

Теоретическая часть

1. Определение точки локального экстремума.

2. Необходимое условие экстремума.

3. Теоремы о первом и втором достаточных условиях экстремума.

4. Определение точки перегиба и необходимое условие перегиба.

5. Теоремы о первом и втором достаточных условиях перегиба.

6. Определение асимптоты кривой (наклонной, вертикальной и горизонтальной).

7. Теорема о необходимом и достаточном условиях существования наклонной асимптоты.

Практическая часть

1. Найти промежутки возрастания и убывания функции и выделить её точки экстремума /2, стр. 127/.

1.1. №107 (з). 1.2. №107 (г). 1.3. №107 (д).

1.4. №107 (е). 1.5. №107 (и). 1.6. №107 (к).

2. Найти наклонную асимптоту кривой /2, стр. 87/.

2.1. №174 (а). 2.2. №174 (б). 2.3. №174 (в).

2.4. №174 (г). 2.5. №174 (д). 2.6. №174 (ж).