
- •Предисловие Задания лабораторных работ составлены согласно разделам дисциплины «Математический анализ» за первый семестр в соответствии с её линией курса, приведенной в рабочей программе.
- •Лабораторная работа №1
- •Лабораторная работа №2
- •Лабораторная работа №3
- •Вычислить следующие пределы /2, стр.79-83/:
- •Лабораторная работа №8
- •Лабораторная работа №10
- •Исследовать функции и начертить их графики /2, стр.132/.
- •Лабораторная работа №14
- •Литература
- •Семестр: первый
Лабораторная работа №3
Тема: Метод математической индукции. Бином Ньютона
Теоретическая часть
Метод математической индукции.
Арифметическая и геометрические прогрессии и их суммы.
Бином Ньютона. Свойства биномиальных коэффициентов.
Среднее арифметическое, среднее геометрическое, среднее гармоническое и среднее квадратичное
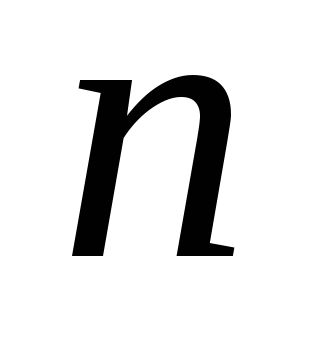 чисел и их связь.
чисел и их связь.
Практическая часть
Доказать методом математической индукции
1.1.
![]() .
.
1.2.
![]() .
.
1.3.
![]() .
.
1.4.
![]() .
.
1.5.
![]() .
.
1.6.
![]() .
.
Решить уравнения или уравнение и неравенство
а)
 ;
б)
;
б)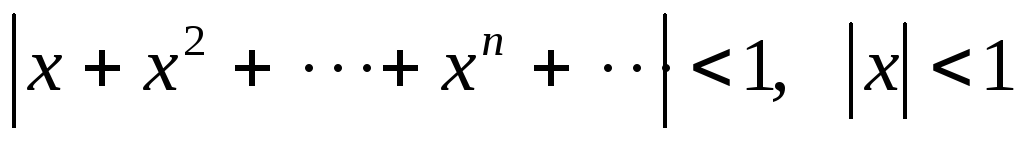 .
.
а)
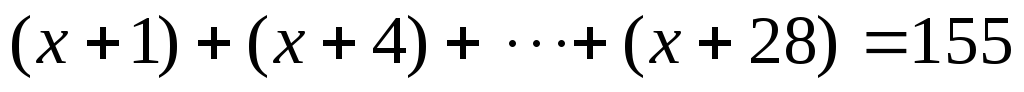 ;
б)
;
б)
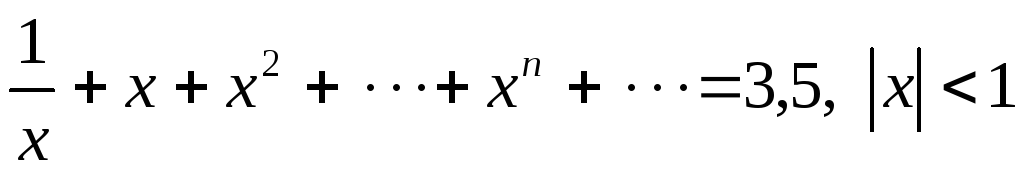 .
.
а)
 ;
б)
;
б)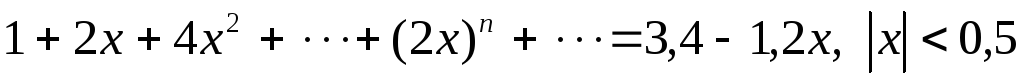 .
.
2.4.
а)
![]() ;
б)
;
б)![]() .
.
2.5.
а)
![]() ;
б)
;
б)![]() .
.
2.6.
а)
![]() ;
б)
;
б)![]()
Написать разложение бинома
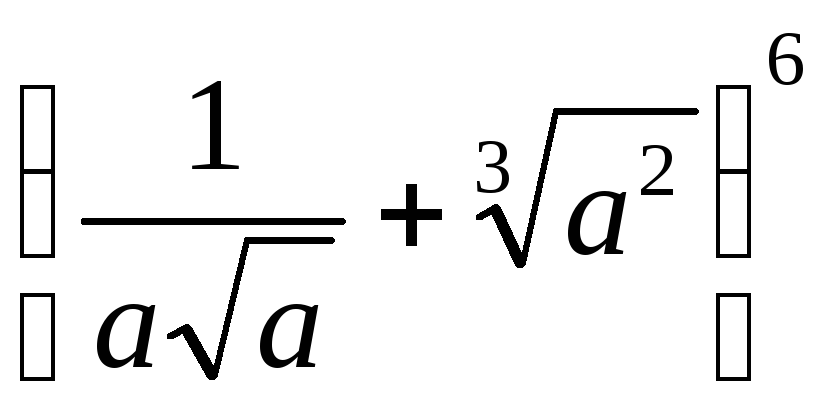 .
3.2.
.
3.2.
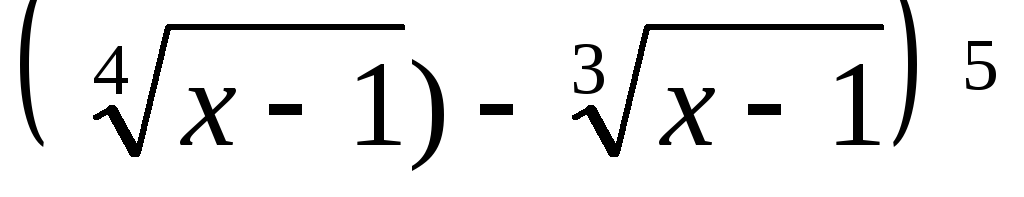 .
3.3.
.
3.3.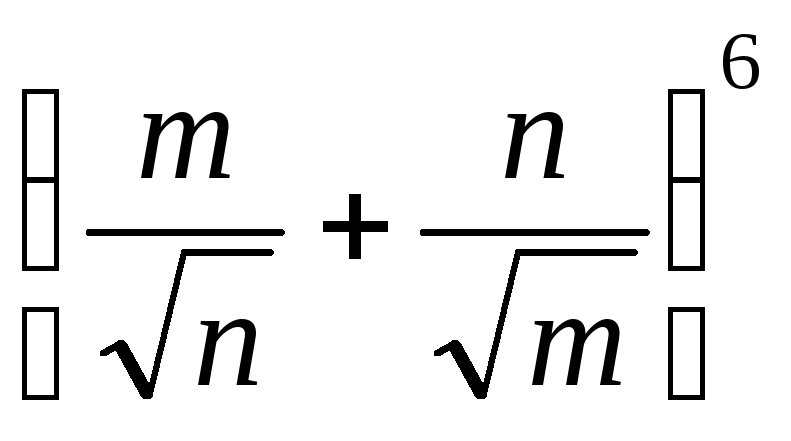 .
.
 .
3.5.
.
3.5.
 .
3.6.
.
3.6.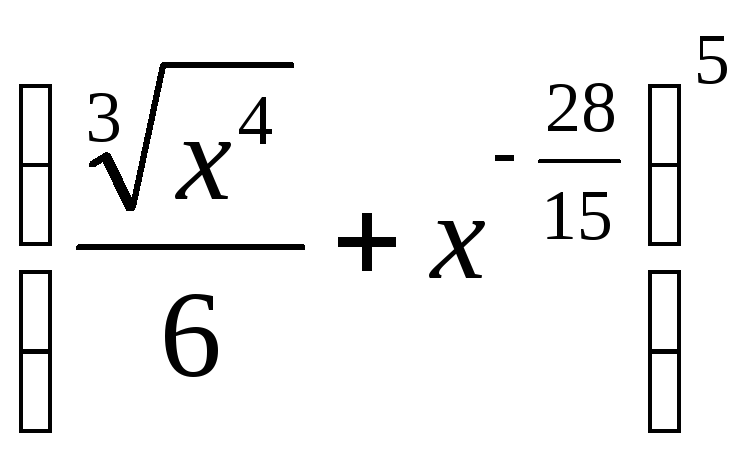 .
.
Найти
член разложения
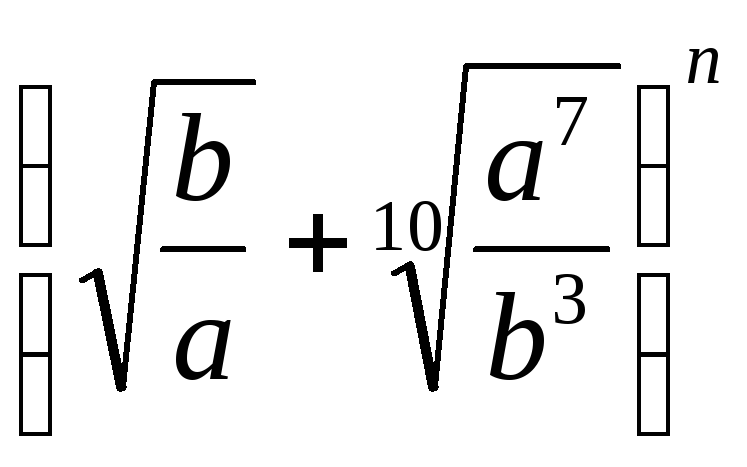 ,
содержащий
,
содержащий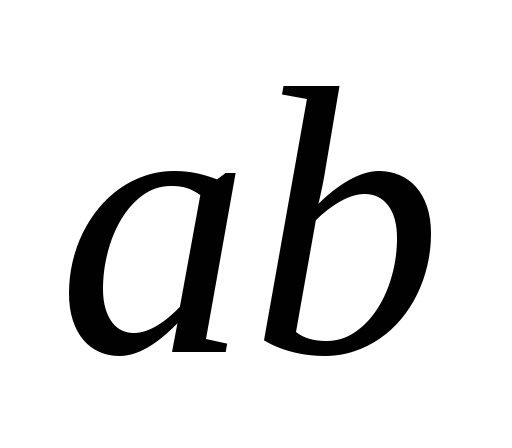 .
.
член разложения
 ,
не содержащий
,
не содержащий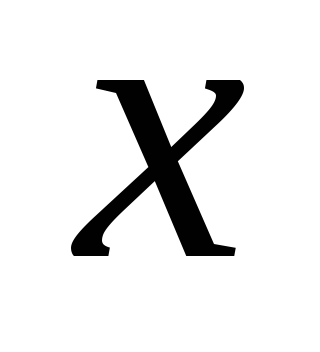 .
.
член разложения
 ,
являющийся целым.
,
являющийся целым.
член разложения
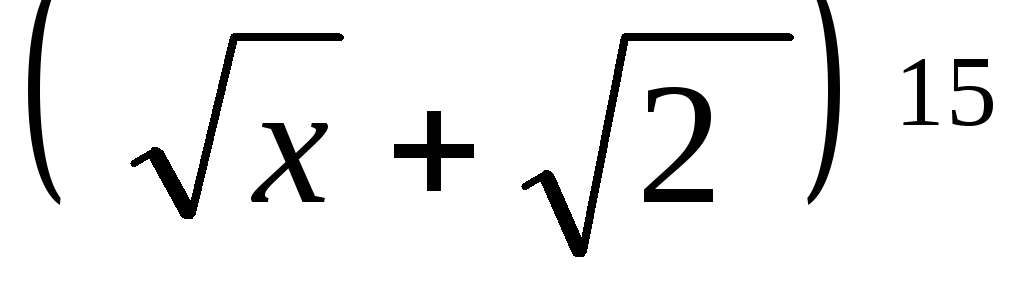 ,
содержащий
,
содержащий .
.
член разложения
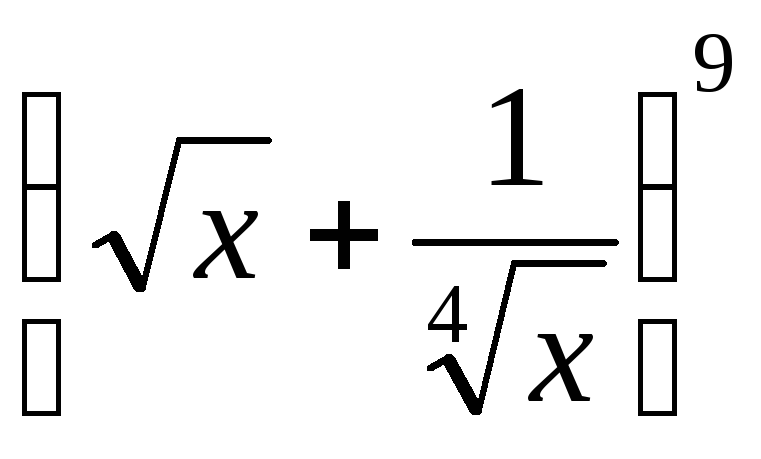 ,
не содержащий
,
не содержащий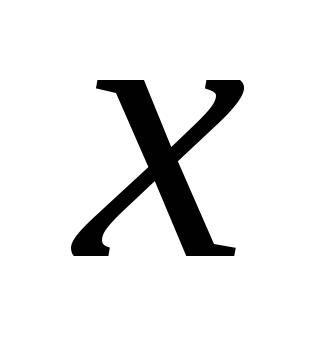 .
.
член разложения
 ,
являющийся целым.
,
являющийся целым.
Решить следующую задачу:
5.1.
Каков наибольший коэффициент разложения
![]() ,
если сумма всех коэффициентов равна
4096?
,
если сумма всех коэффициентов равна
4096?
5.2.
При каких значениях
![]() четвертый член разложения
четвертый член разложения![]() больше двух соседних с ним членов?
больше двух соседних с ним членов?
5.3.
В какую натуральную степень следует
возвести бином![]() ,
чтобы отношение четвертого члена
разложения к третьему равнялось бы
,
чтобы отношение четвертого члена
разложения к третьему равнялось бы![]() ?
?
5.4.
Сумма нечетных биномиальных коэффициентов
разложения
![]() равна
512. Найти слагаемое, не содержащее
равна
512. Найти слагаемое, не содержащее![]() .
.
5.5.
Найти показатель
![]() бинома
бинома![]() ,
зная, что десятый член разложения имеет
наибольший коэффициент.
,
зная, что десятый член разложения имеет
наибольший коэффициент.
5.6.
Найти пятый член разложения
![]() ,
если отношение третьего члена ко второму
равно
,
если отношение третьего члена ко второму
равно![]() .
.
Лабораторная работа №4
Тема: Числовые последовательности
Теоретическая часть
Определение числовой последовательности.
Определения монотонной (убывающей, возрастающей), ограниченной (неограниченной) последовательностей.
Определение предела числовой последовательности. Определения сходящейся и фундаментальной последовательностей.
Теорема о сходимости монотонной числовой последовательности.
Определение системы вложенных отрезков. Лемма Гейне-Бореля о конечном покрытии.
Теорема Больцано-Вейерштрасса о выделении сходящейся подпоследовательности.
Критерий Коши существования предела числовой последовательности.
Практическая часть
Доказать следующее равенство /3/:
№60. 1.2. №61. 1.3. №59. 1.4. №63. 1.5. №65. 1.6. №66.
2-4. Найти пределы последовательностей /4/.
2.1. №8.27 (1); 3.1. №8.28 (6); 4.1. №8.34 (1).
2.2. №8.27 (5); 3.2. №8.28 (7); 4.2. №8.34 (2).
2.3. №8.27 (6); 3.3. №8.28 (8); 4.3. №8.34 (3).
2.4. №8.27 (7); 3.4. №8.28 (9); 4.4. №8.34 (5).
2.5. №8.27 (8); 3.5. №8.28 (10); 4.5. №8.34 (6).
2.6. №8.27 (4); 3.6. №8.28 (4); 4.6. №8.34 (7).
5. Пользуясь критерием Коши, доказать сходимость последовательности.
5.1.
![]() .
5.2.
.
5.2.![]() .
.
5.3.
![]() .
5.4.
.
5.4.![]() .
.
5.5.
![]() .
5.6.
.
5.6.![]() .
.
6. Пользуясь теоремой о существовании предела монотонной последовательности, доказать сходимость последовательности.
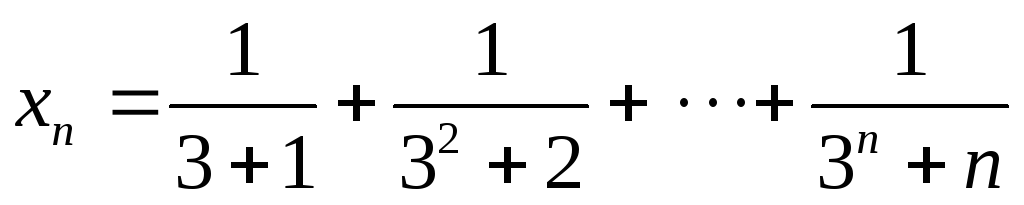 .
.
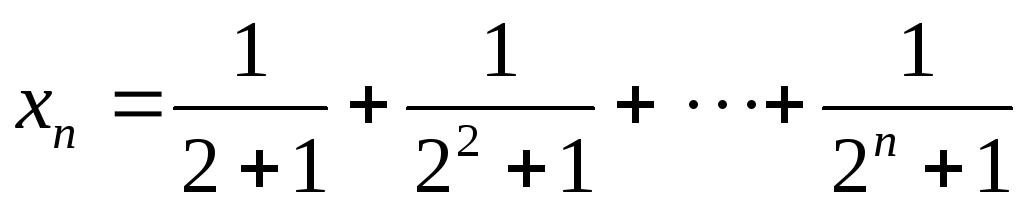 .
.
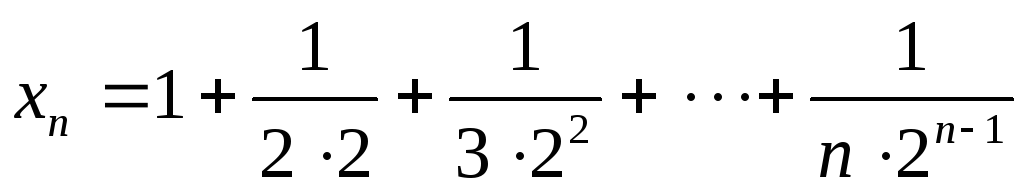 .
.
 .
.
6.6.
![]() .
.
Лабораторная работа №5
Тема: Предел функции в точке
Теоретическая часть
Определение предела функции в точке по Гейне.
Определение предела функции в точке по Коши.
Определение одностороннего предела функции в точке (справа, слева).
Определения пределов вида
 по Коши.
по Коши.Теорема об эквивалентности определений предела функции в точке по Гейне и по Коши.
Критерий Коши существования предела функции в точке.
Теорема о существовании односторонних пределов в точке у монотонной на отрезке функции.
Практическая часть
Сформулировать утверждение и начертить схематический чертеж.
1.1.
![]() .
1.2.
.
1.2.![]() .
1.3.
.
1.3.![]() .
.
1.4.
![]() .
1.5.
.
1.5.![]() .
1.6.
.
1.6.![]() .
.
Сформулировать утверждение и начертить схематический чертеж /3/.
2.1. №404 (а). 2.2. №404 (б). 2.3. №405 (б).
2.4. №407 (а). 2.5. №406 (б). 2.6. №407 (в).
Найти односторонние пределы функции при
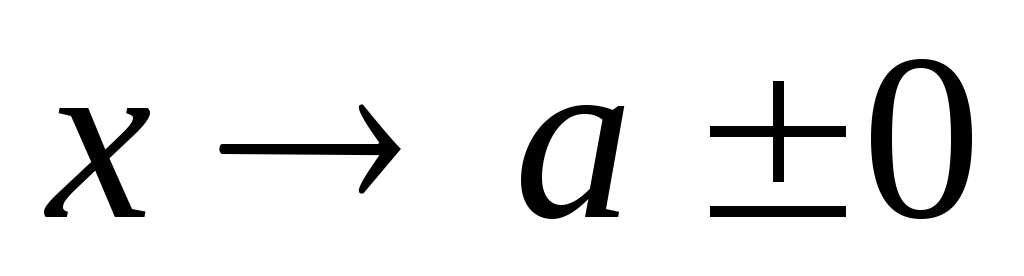 ,
если
,
если
3.1.
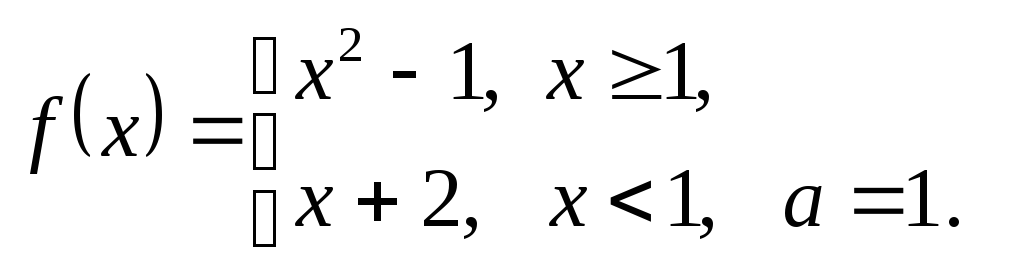 3.2.
3.2.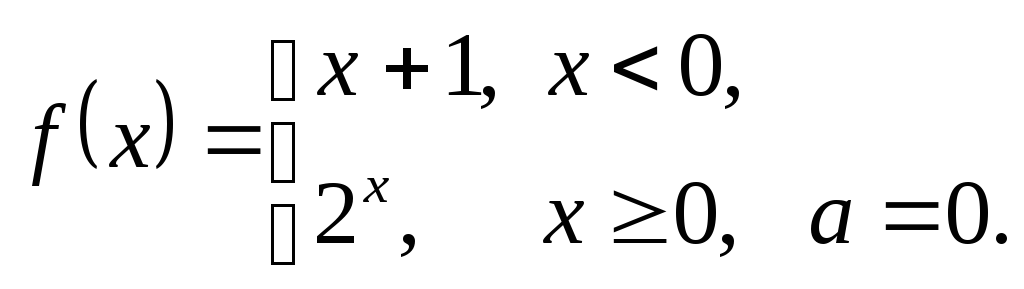
3.3.
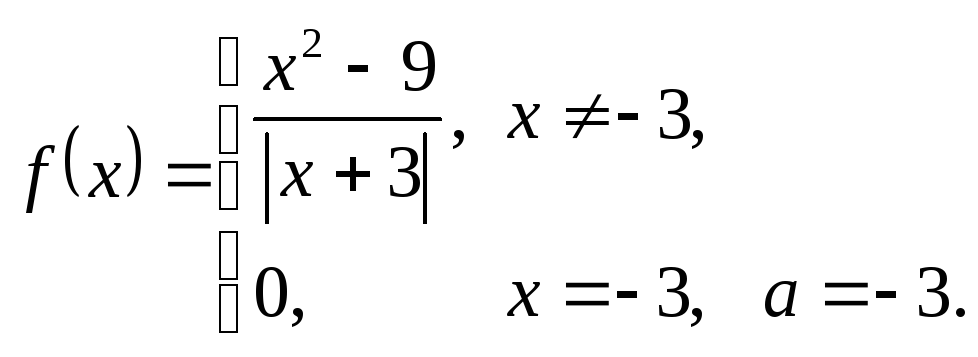 3.4.
3.4.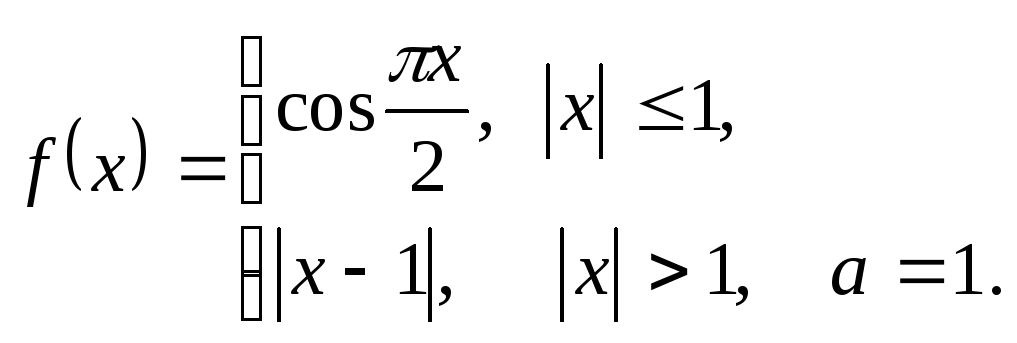
3.5.
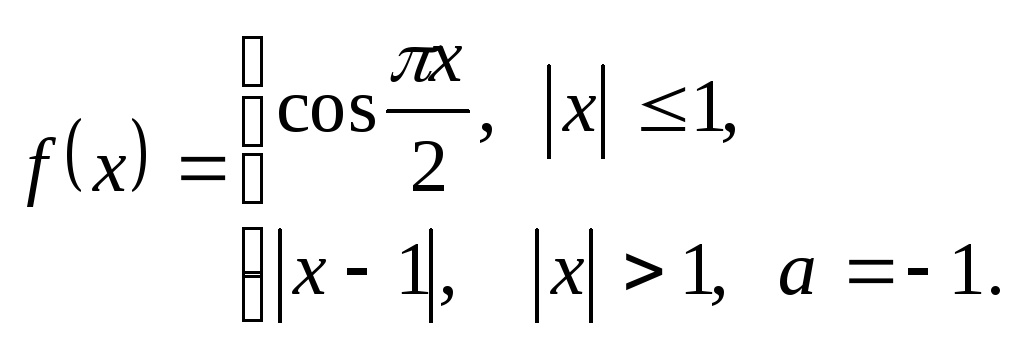 3.6.
3.6.![]()
![]() .
.
Доказать, что функция не имеет предела в точке
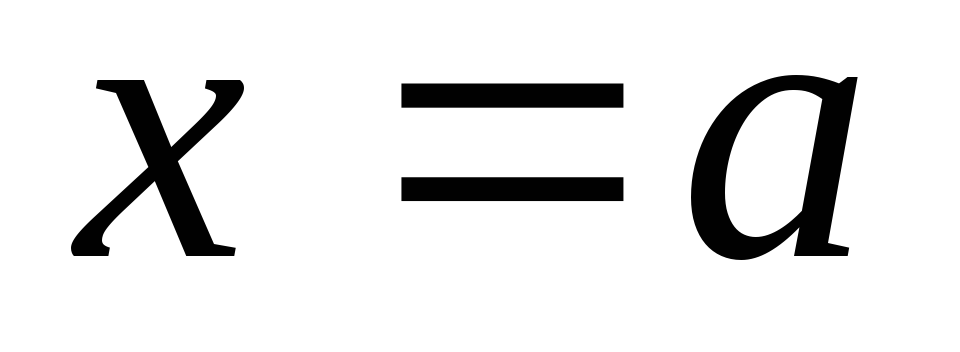 ,
если
,
если
4.1.
![]() 4.2.
4.2.
![]()
4.3.
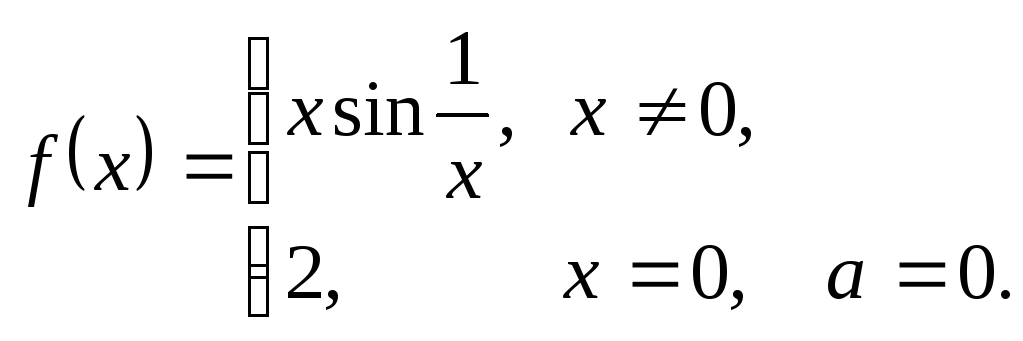 4.4.
4.4.![]()
4.5.
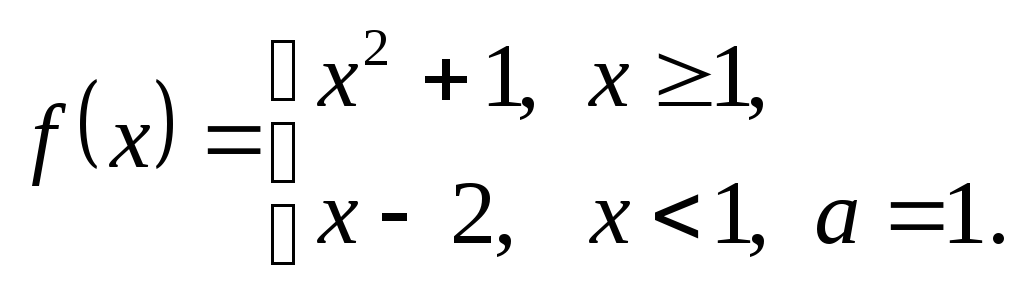 4.6.
4.6.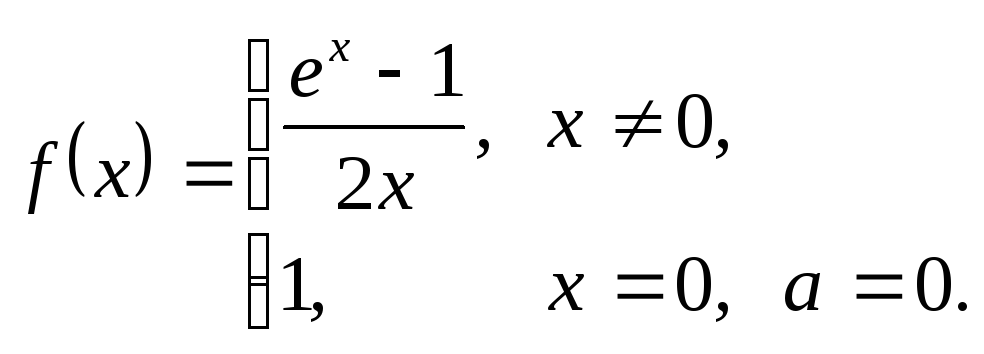
Найти предел функции /3/.
5.1. №595 (а). 5.2. №596 (а). 5.3. №595 (б).
5.4. №596 (б). 5.5. №597 (а). 5.6. №597 (б).
Лабораторная работа №6
Тема: Техника вычисления пределов
Теоретическая часть
Первый замечательный предел.
Второй замечательный предел (в двух формах).
Сравнение функций:
а) функции одного порядка;
б) эквивалентность функций;
в) функции более высокого порядка.
О-символика и её свойства.
Таблица эквивалентностей бесконечно малых функций.
Практическая часть
