
Рабочая тетрадь по начертательной геометрии
.pdf
Министерство сельского хозяйства Российской Федерации Департамент научно-технологической политики и образовании
Федеральное государственное образовательное учреждение высшего профессионального образования
«ЧЕЛЯБИНСКИЙ ГОСУДАРСТВЕННЫЙ АГРОИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ»
Кафедра начертательной геометрии и инженерной графики
УТВЕРЖДАЮ Проректор по УР А.А. Патрушев
РАБОЧАЯ ТЕТРАДЬ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Для студентов I курса факультета ЭАСХП
Челябинск 2008
Рабочая тетрадь по начертательной геометрии предназначена для студентов I курса факультета ЭАСХП
Составители:
Назмутдинова Н.И. - старший преподаватель кафедры графики ЧГАУ Торбеев И.Г. - к. т. н., доцент кафедры графики ЧГАУ Лещенко Г.П. – к.т.н., доцент кафедры графики ЧГАУ
Рецензенты:
Швайгер А.М. - к.т.н., профессор кафедры графики ЮУрГУ Четыркин Ю.Б. - к. т. н., доцент, декан факультета МСХ ЧГАУ
Ответственный за выпуск:
Торбеев И.Г. - доцент., к. т. н., зав. кафедрой инженерной графики и начертательной геометрии Печатается по решению издательского совета ЧГАУ
© Челябинский Государственный Агроинженерный Университет, 2008 г.
Методические указания
Рабочая тетрадь предназначена студентам для решения задач на практических занятиях под руководством препода-
вателя и самостоятельного решения в домашних условиях. Решение выполняется непосредственно в рабочей тетради.
Заданы условия задач, исходный чертеж, оставлено место для решения. Графические построения необходимо выполнять карандашом марки М или МТ с помощью чертежных инструментов. Все вспомогательные точки, линии, плоскости должны быть обозначены. Обозначение и надписи выполняются четко и аккуратно стандартным шрифтом (ГОСТ 2.30484). Искомые геометрические фигуры (ответ задачи) обвести цветным карандашом.
В данной рабочей тетради усилена тема “Поверхности, принадлежность линии и точки поверхности”.
Для некоторых типов задач даны методические указания.
Кпрактическому занятию студент должен:
1.Закончить решение задач предыдущего занятия.
2.Проработать по конспекту лекций и предлагаемой литературе теоретический материал, относящийся к теме занятия.
3.Приступая к решению задачи, внимательно прочитать условие и составить пространственный алгоритм (ПА), а затем
и графический алгоритм (ГА) её решения.
К экзамену студент должен:
1.Решить задачи в рабочей тетради.
2.Выполнить и защитить домашние графические работы.
3.Выполнить аудиторные контрольные работы.
На экзамен студент приходит с зачетной книжкой, с данной рабочей тетрадью, с графическими работами и инстру-
ментами.
4
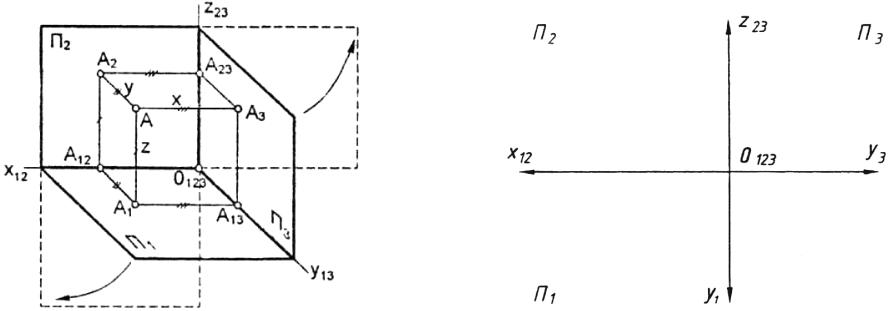
1. Комплексный чертеж точки. Осный и безосный способ изображения
1.1 Осный способ изображения Задача 1 На аксонометрическом чертеже нанести координаты точки А. Значения координат (в мм) занести в табли-
цу. Коэффициенты искажения по осям X, Z принять равными 1, по оси Y=0,5. Построить комплексный чертеж точки А.
|
|
Записать название плоскостей проекций: |
Записать название проекций точки А: |
XА (широта) |
|
||
|
|
|
|
|
|
П1-_________________________________ |
А1-______________________________________ |
YA (глубина) |
|
||
|
|
|
|
|
|
П2-_________________________________ |
А2-______________________________________ |
ZА (высота) |
|
||
|
|
|
|
|
|
П3-_________________________________ |
А3-______________________________________ |
|
|
5
Задача 2 1) На комплексном чертеже (чертеж к задаче1) обозначить отрезки, определяющие расстояния точки А
до плоскостей проекций:
до плоскости П1 (высота)_______________________________________
до плоскости П2 (глубина)______________________________________
до плоскости П3 (широта)_______________________________________
2) Записать условия связи между проекциями точки на комплексном чертеже:
1_______________________________________________________________________________________________
_______________________________________________________________________________________________
2_______________________________________________________________________________________________
_______________________________________________________________________________________________
3_______________________________________________________________________________________________
_______________________________________________________________________________________________
3)Сколько проекций точки определяет её положение в пространстве?
_______________________________________________________________________________________________
4)Можно ли по двум проекциям точки построить её третью проекцию?
_______________________________________________________________________________________________
5)Как может быть задана точка?
_______________________________________________________________________________________________
6

1.2 Безосный способ изображения
Плоскости проекций не фиксируются, оси становятся неопределенными и на чертеже не наносятся. Если заданы две проекции (например, горизонтальная и фронтальная) системы взаимосвязанных точек, то третья проекция каждой из них строится следующим образом. Одна из точек, например, А, принимается за базовую. Положение проекций каждой из ос-
тальных точек определяется по разности координат, которые не зависят от положения плоскостей проекций.
Задача 3 Построить три проекции треугольника АВС по координатам его вершин, вычисленным относи-
тельно заданной вершины А(А1,А2); В(-25;15;15);
С(-15;30;-15).
7
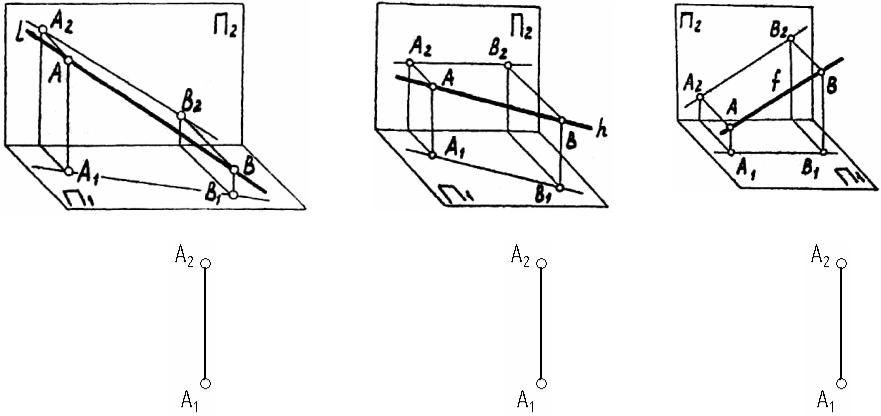
2. Комплексный чертеж прямой
Задача 4 Построить комплексный чертеж прямой по наглядному изображению и разности координат двух её точек А и В. В каждом случае записать название прямой. Указать на чертеже линий уровня натуральные величины отрезков
[AB] и углы их наклона к плоскостям проекций (α, β, γ).
а) l(A,B) -_______________________ б) h(A,B) -_________________________ в) f(A,B) -__________________________
XA-XB=35 |
XA-XB=35 |
XA-XB=35 |
YA-YB=15 |
YA-YB=15 |
YA-YB=0 |
ZA-ZB=20 |
ZA-ZB=0 |
ZA-ZB=20 |
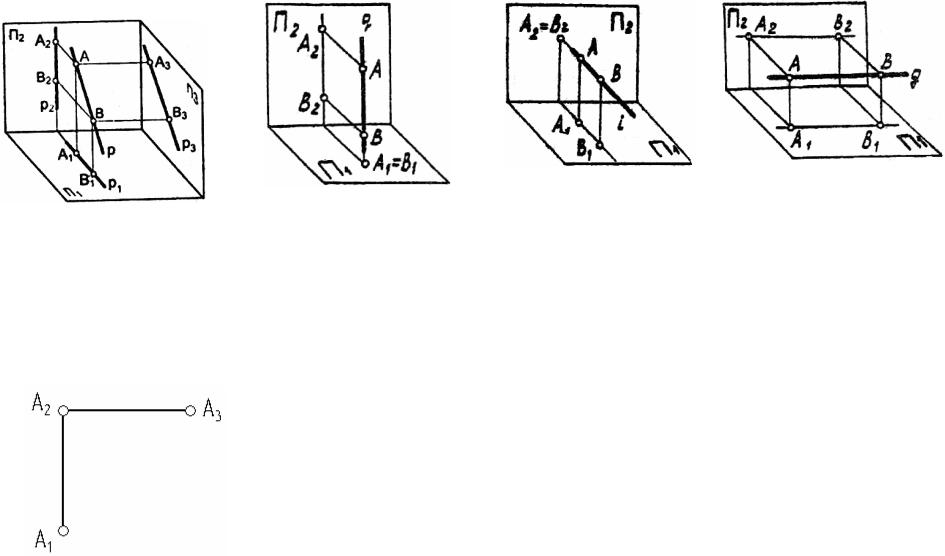
г) p(A,B) -________________ д) q(A,B) -________________ е) i(A,B) -________________ ж) g(A,B) -________________
XA-XB=0 |
XA-XB=0 |
XA-XB=0 |
XA-XB=35 |
YA-YB=15 |
YA-YB=0 |
YA-YB=15 |
YA-YB=0 |
ZA-ZB=20 |
ZA-ZB=20 |
ZA-ZB=0 |
ZA-ZB=0 |
9

2.1 Определение длины отрезка прямой и углов его наклона к плоскостям проекций способом прямоугольного треугольника
Натуральная величина отрезка прямой общего положения на комплексном чертеже может быть определена как ги-
потенуза прямоугольного треугольника, одним катетом которого будет проекция отрезка, а другим - разность недос-
тающих координат концов отрезка. |
Задача 6 К мачте АВ(А1В1, А2В2) прикреплены растяжки: |
|
АС(А1С1, А2С2), АD(А1D1, А2D2) и АЕ(А1Е1, А2Е2). Опреде- |
|
лить длины и углы наклона растяжек к горизонтальной |
|
плоскости. На каждой растяжке найти точку, удаленную на |
|
расстояние 20 мм от точки А. |
Задача 5 На отрезке[AB] найти точку С, отстоящую от точки А на 40 мм.
10
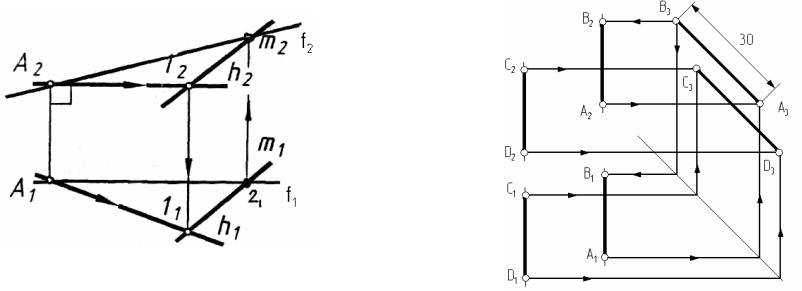
2.2 Относительное положение прямых линий
Две прямые линии могут пересекаться (иметь общую точку), скрещиваться и быть параллельными. Если прямые параллельны, то параллельны их одноименные проекции. Одна из скрещивающихся прямых может быть выше (относи-
тельно П1) и дальше (относительно П2). Положение скрещивающихся прямых определяется с помощью горизонтально и
фронтально конкурирующих точек соответственно. |
Задача Заданы C2D2, C1D1 и А2А1, через точку А |
Задача Через точку А провести горизонталь h, |
провести отрезок [AB] длиной 30 мм параллельный |
и фронталь f пересекающую прямую m. |
прямой CD. |
Алгоритм решения: |
|
Построение горизонтали начинается с её фронтальной проекцией h2 |
|
из точки А под прямым углом к вертикальной линии связи. Отмечаем |
Алгоритм решения: |
фронтальную проекцию 12 точки пересечения горизонтали и прямой |
1. Строят C3D3 и А3. |
m. По линии связи по принадлежности находим горизонтальную проек- |
2. Через А3 строят А3В3׀׀С3D3, причем |
цию точки пересечения 11, через которую проводим h1. Построение |
А3В3=30 мм. |
фронтали, начинают с её горизонтальной проекции. |
3. Строят В1 и В2. |
11
