Содержание заданий

1. Построить статистическое распределение выборки.

2. Вычислить оценки математического ожидания и дисперсии.

3. Построить гистограмму относительных частот, установить статистический (эмпирический) закон распределения и записать его функцию плотности. С помощью критерия (Пирсона) проверить гипотезу о согласии эмпирического закона распределения случайной величиныс нормальным законом распределения (законом Гаусса).

4. Построить кривую нормального распределения, приняв за параметры кривой найденные оценки математического ожидания и дисперсии (желательно на одном чертеже с гистограммой).

5. Вычислить доверительный интервал для математического ожидания и дисперсии.

Вопросы для повторения и подготовки к выполнению задания

1. Назовите виды зависимости между двумя величинами, охарактеризуйте каждый из видов.

2. Перечислите числовые характеристики дискретных и непрерывных случайных величин.

3. Запишите формулы, по которым определяют числовые характеристики дискретных и непрерывных случайных величин.

4. Сформулируйте определение статистической гипотезы, приведите примеры статистических гипотез.

5. Сформулируйте определение гистограммы частот, относительных частот.

6. Каким образом применяются гистограммы в статистических исследованиях.

7. Назовите виды оценок параметров гипотетического распределения, охарактеризуйте каждый из видов.

8. Раскрыть применение каждого вида оценок параметров гипотетического распределения .

9. Приведите примеры статистических критериев проверки гипотез. Запишите алгоритм проверки статистических гипотез посредством критерия Пирсона .

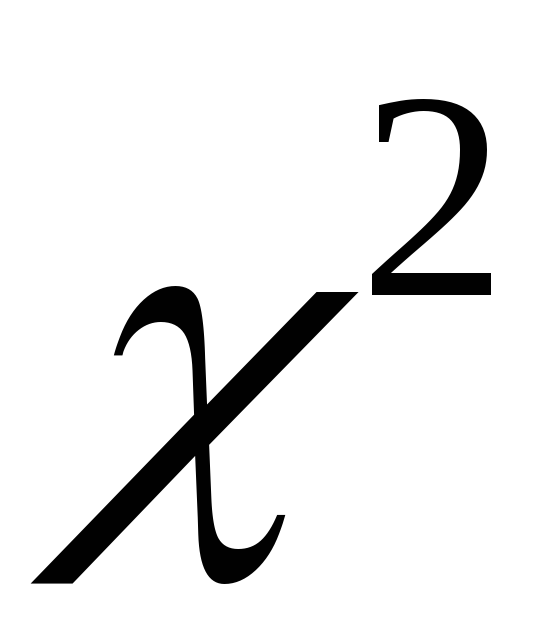Пример выполнения задания

Измерен характерный размер деталей , обрабатываемых на некотором станке. Замерено 60 деталей. Данные замеров приведены в таблице 1.

Таблица 1

72,58	72,58	72,47	72,66	72,36
72,35	72,47	72,49	72,35	72,50
72,33	72,54	72,28	72,50	72,43
72,54	72,24	72,47	72,69	72,46
72,24	72,38	71,95	72,54	72,56
72,42	72,70	72,18	72,48	72,48
72,43	72,41	72,51	72,20	72,28
72,56	72,14	72,37	72,48	72,64
72,34	72,29	72,14	72,66	72,72
72,38	72,31	72,42	72,64	72,35
72,56	72,30	72,36	72,73	72,60
72,32	72,28	72,28	72,43	72,46

Обработайте результаты этого опыта по следующему плану:

1. Составить статистическое распределение выборки.

2. Вычислить для данной выборки несмещенные оценки математического ожидания и дисперсии.

3. Построить гистограмму относительных частот, установив статистический (эмпирический) закон распределения и запишем его функцию плотности. С помощью критерия (Пирсона) проверим гипотезу о согласии эмпирического закона распределения случайной величиныс нормальным законом распределения (законом Гаусса).

4. Построить кривую нормального распределения, приняв за параметры кривой найденные оценки математического ожидания и дисперсии (желательно на одном чертеже с гистограммой).

5. Вычислить доверительные интервалы для математического ожидания и дисперсии.

Выполнение задания

1. Найдем статистическое распределение выборки:

xi	71,95	72,14	72,18	72,20	72,24	72,28
ni	1	2	1	1	2	4

xi	72,29	72,30	72,31	72,32	72,33	72,34
ni	1	1	1	1	1	1

xi	72,35	72,36	72,37	72,38	72,41	72,42
ni	3	2	1	2	1	2

xi	72,43	72,46	72,47	72,48	72,49	72,50
ni	3	2	3	3	1	2

xi	72,51	72,54	72,56	72,58	72,60	72,64
ni	1	3	3	2	1	2

xi	72,64	72,66	72,69	72,7	72,72	72,73
ni	2	2	1	1	1	1

Объем выборки .

2. Преобразуем данную выборку в вариационный (интервальный) ряд. Диапазон изменения случайной величины в выборке объемаделим наинтервалов. Число интервалов определяется по следующей полуэмпирической формуле Стерджесса

с округлением до ближайшего целого.

В нашем примере

.

Длину каждого частичного интервала берем одинаковой: , где,– наибольший и наименьший элементы выборки; величинувыбираем с точностью выборки и округляем в сторону завышения.

В нашем примере

.

Границы интервалов вычисляем по формуле

, где i = 0, 1, 2, .., k-1; .

По протоколу выборки подсчитываем количество элементов , попавших вi-й интервал (частота интервала). Если элемент совпадает с границей интервала, то он относится к предыдущему интервалу.

Вычисляем относительные частоты интервалов:

, где i = 0, 1, 2, ..., k.

Полученные данные вносим в таблицу 2.

Таблица 2

Номер интервала i	Частичный интервал	Сумма частот вариант частичного интервала	Относительная частота	Плотность относительной частоты
1	71,95 – 72,07	1		0,14
2	72,07 – 72,19	3		0,42
3	72,19 – 72,31	10		1,39
4	72,31 – 72,43	17		2,36
5	72,43 – 72,55	15		2,08
6	72,55 – 72,67	10		1,39
7	72,67 – 72,79	4		0,56

Вычисляем оценки математического ожидания и дисперсии

по формулам

; , (1)

где – частота вариантыв выборке объема.

Если объем выработки велик, то вычисление точечных оценок математического ожидания и дисперсиипо формулам (1) громоздко. Для сокращения вычислений элементам выборки, попавшим вi – й интервал, припишем значения, равные серединам интервалов:

, где i = 1, 2, … k.

Для упрощения дальнейших выкладок варианты заменяем новымипо формуле, (i = 1, 2, … k), где называется условной вариантой,c - ложным нулем (новым началом отсчета).

Замечание 1. Если число интервалов нечетное, то в качестве ложного нуля берем середину среднего интервала, если четное, то середину того интервала, у которого больше частота.

Замечание 2. Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю.

Значения ивносим в таблицу 3. Теперь вычисления оценок производим с помощью определений математического ожидания и дисперсии. Оценка математического ожидания

,

где .

Итак, (3) – рабочая формула для оценки математического ожидания.

Для вычисления оценки подсчитываем произведенияии вносим в таблицу 3.

Оценка дисперсии определяется по формуле где;.

Итак, (4) - рабочая формула для дисперсии.

Для вычисления дисперсии подсчитаем произведенияии внесем в таблицу 3.

Таблица 3

Номер интервала	Частичный интервал	Сумма частот вариант частичного интервала	Относительная частота	Середина интервала
1	71,95 – 72,07	1		72,01	-3			0,14
2	72,07 – 72,19	3		72,13	-2			0,42
3	72,19 – 72,31	10		72,25	-1			1,39
4	72,31 – 72,43	17		72,37	0			2,36
5	72,43 – 72,55	15		72,49	1			2,08
6	72,55 – 72,67	10		72,61	2			1,39
7	72,67 – 72,79	4		72,73	3			0,56
		60	1

В нашем примере

.

- оценка математического ожидания.

Эта оценка занижает дисперсию генеральной совокупности, поэтому вводится поправочный коэффициент и получается так называемая несмещенная оценка дисперсии:

, где – объем выборки.

В нашем примере

.

Далее вычисляем оценку среднего квадратического отклонения:

В нашем примере .

- оценка среднего квадратического отклонения.

Для сравнения подсчитаем по «правилу». Так как для случайной величины, имеющей нормальное распределение, почти все рассеивания укладываются на участке, то с помощью «правила» можно ориентировочно определить оценку среднего квадратического отклонения случайной величины. Берем максимальное практически возможное отклонение от среднего значения и делим его на три.

В нашем примере ;;

;

;

Построение гистограммы относительных частот

Гистограммой называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной , а высоты равны(плотность относительной частоты).

Для построения гистограммы данные берем из таблицы 2.

Строим точки с координатами . Если построенные точки гистограммы соединить плавной линией (рис. 1), то эта линия будет аналогом плотности распределения случайной величины. Следовательно, по виду гистограммы можно выдвинуть предположение о виде закона распределения случайной величины.

В нашем примере по виду гистограммы (рис. 1) выдвигаем гипотезу о нормальном распределении (или о распределении, близком к нормальному) случайной величины с плотностью

, (5)

где - оценка среднего квадратического отклонения,- оценка математического ожидания.

В дальнейшем функцию (5) будем называть теоретическим законом распределения.

Рис.1

Проверим гипотезу о нормальном распределении случайной величины.

Ввиду ограниченного числа наблюдений статистический закон распределения обычно в какой-то мере отличается от теоретического, даже если предположение о законе распределения сделано правильно. В связи с этим возникает необходимость решить следующую задачу: является ли расхождение между статистическим и теоретическим законами распределения следствием ограниченного числа наблюдений или оно является существенным и связано с тем, что действительное распределение случайной величины не соответствует выдвинутой гипотезе.

Чтобы с помощью критерия Пирсона проверить гипотезу о нормальном распределении случайной величины , нужно вычислить теоретические частоты:, где

. (6)

Для проверки гипотезы о нормальном распределении рассматриваемой величины заполняем таблицу 4.

1. Интервалы, содержащие малочисленные эмпирические частоты, (), следует объединить, а соответствующие частоты сложить (в нашем примере после объединения число интервалов).

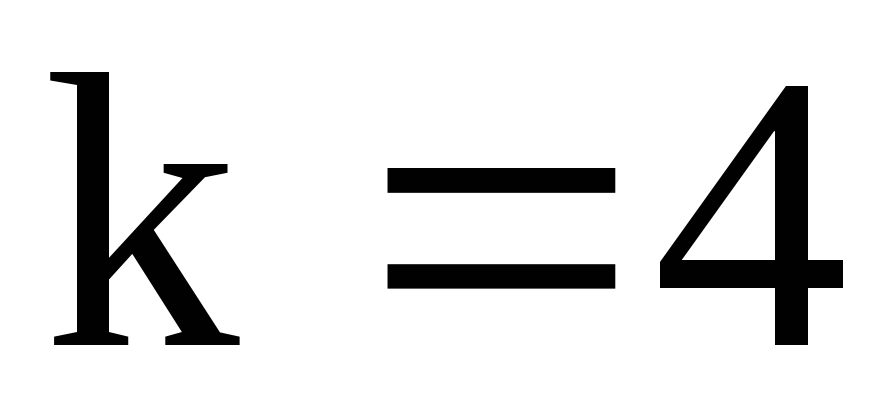2. Вычисляем вероятности 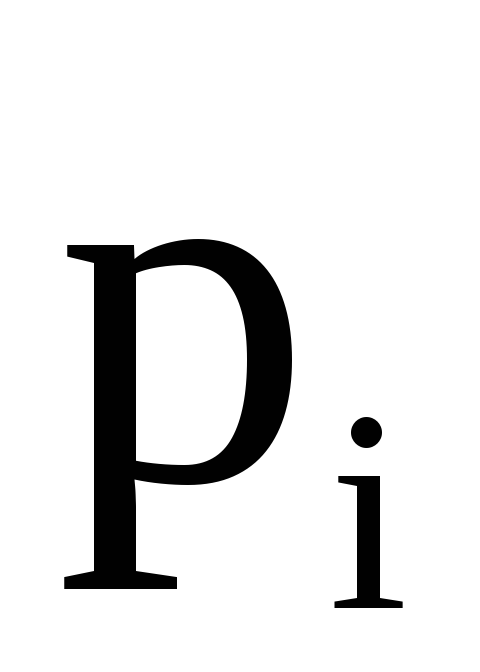попадания варианты в каждом интервале:

,

где – номер интервала,- функция Лапласа;

, причем .

3. Вычисляем ис учетом объединения интервалов.

4. Для проверки гипотезы о нормальном распределении случайной величины в качестве меры расхождения между теоретическим и статистическим распределениями выберем случайную величину (хи-квадрат)

(7)

(8)

Случайная величина распределена по законус параметром, называемым числом степеней свободы. Число степеней свободы вычисляем по формуле, где- число классов выборки (после объединения);- число параметров предполагаемого распределения, оценки которых получены по данным выборки.

Из формулы (7) следует, что расхождение между статистическим и теоретическим распределениями является несущественным, если величина не превышает некоторого критического значения. Чтобы найти, задаемся достаточно малой вероятностью, например,, называемой уровнем значимости:.

Для критерия имеются таблицы, из которых по заданному уровню значимости и числу степеней свободынаходим критическое значение.

План действий по применению критерия :

1. По данным выборки вычислим значение критерия по формуле (7) и обозначим полученное число через (хи-квадрат статистическое).

В нашем примере .

2. По заданному уровню значимости и числу степеней свободыпо таблице находим. В нашем примере дляипо таблице находим.

3. Если , то гипотезу о нормальном распределении отвергаем, т.е. теоретическое распределение не совпадает с эмпирическим (статистическим).

4. Если , то нет оснований отвергать выдвинутую гипотезу о нормальном распределении случайной величиныи с надежностьюможно считать правдоподобной, не противоречащей опытным данным.

В нашем примере .

Таблица 4

Номер интер- вала
1	71,95	72,31	-0,48	-0,12	-3	-0,75	-0,49865	-0,2734
2	72,31	72,43	-0,12	0	-0,75	0	-0,2734	0
3	72,43	72,55	0	0,12	0	0,75	0	0,2734
4	72,55	72,79	0,12	0,36	0,75	2,25	0,2734	0,4878

Номер интер- вала
1	0,22525	14	0,2333	13,515	0,485	0,2352	0,0174
2	0,2734	17	0,2833	16,404	0,596	0,3552	0,0217
3	0,2734	15	0,2500	16,404	-1,404	1,9712	0,1202
4	0,2144	14	0,2333	12,864	1,136	1,2905	0,1003
	1	60	1				0,2595

Теоретическая плотность распределения имеет вид

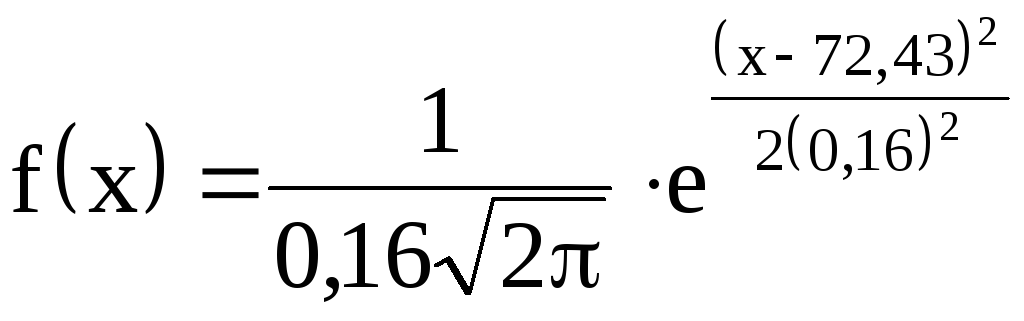. (9)

Построим график этой функции. Для этого возьмем 7 точек с абсциссами (=1,2,…,7) из таблицы 3 и вычислим ординаты этих точек. Для удобства составим таблицу 5.

Таблица 5

Номер интер- вала
1	72,01	-0,42	0,1760	3,52	0,0296	0,074
2	72,13	-0,30	0,0900	1,80	0,1650	0,413
3	72,25	-0,18	0,0324	0,65	0,5220	1,305
4	72,37	-0,06	0,0036	0,07	0,9320	2,330
5	72,49	0,06	0,0036	0,07	0,9320	2,330
6	72,61	0,18	0,0324	0,65	0,5220	1,305
7	72,73	0,30	0,0900	1,80	0,1650	0,413

Для более точного построения графика вычислим координаты максимума и точек перегиба графика функции: максимум ; точки перегиба.

В нашем примере максимум , точки перегиба,.

Строим график на рис. 1 (сплошная линия).

Для сравнения значения исведем в таблицу 6.

Таблица 6

Сравнение теоретической и эмпирической плотности распределения случайной величины

	1	2	3	4	5	6	7
	72,01	72,13	72,25	72,37	72,49	72,61	72,73
	0,07	0,41	1,31	2,33	2,33	1,31	0,41
	0,14	0,42	1,39	2,36	2,08	1,39	0,56

Сравнивая значения ординат плотности распределения случайной величины и плотности относительных частот, мы наблюдаем незначительное отклонение этих величин друг от друга, что также свидетельствует о правильности выбора закона распределения.

Вычисление доверительных интервалов для математического ожидания и дисперсии

Оценки параметров инормального распределения, найденные по формулам (3) и (4), называются точечными.

В ряде задач требуется не только найти для параметра подходящее числовое значение, но и оценить его точность и надежность. Для определения точности оценки в математической статистике пользуются доверительными интервалами, а для определения надежности – доверительными вероятностями.

Пусть для параметра получена из опыта оценка. Требуется оценить возможную ошибку при замене параметраего оценкой.

Задаем некоторую достаточно большую вероятность (например,) и находим такое число, для которогоили.

Доверительным называется интервал с центром в точкедлиной, который покрывает неизвестный параметр с заданной надежностью.

Доверительной вероятностью, или надежностью , соответствующей данному доверительному интервалу, называется вероятность того, что истинное значение параметра лежит в этом интервале.

При заданной надежности в равенствечислоопределяет точность оценки. В математической статистике получены формулы для расчета границ доверительных интервалов для различных параметров.

Рассмотрим, как строится доверительный интервал для математического ожидания. Так как гипотеза о нормальном распределении случайной величины не противоречит опытным данным, то будем считать (с некоторым риском), что случайная величинараспределена нормально, причем математическое ожиданиеи среднеквадратическое отклонениеэтого распределения неизвестны.

Доверительный интервал для оценки математического ожидания имеет вид

,

где ,- выборочные оценки математического ожидания и среднего квадратического отклонения, найденные по формулам (3) и (4);– объем выборки.

В каждом учебнике по теории вероятности имеется таблица, пользуясь которой по доверительной вероятности и числу степеней свободынаходим величину, а затем точность оценки:

.

Итак, вычислив по выборке ии найдя по таблице, получим искомый доверительный интервал, покрывающий неизвестное математическое ожидание с заданной надежностью.

В нашем примере для ипо таблице (Е.С. Вентцель, «Теория вероятностей», приложение, таблица 5) находим.

.

Доверительный интервал для математического ожидания имеет вид или.

Рассмотрим, как строится доверительный интервал для среднего квадратического отклонения. Пусть случайная величина распределена нормально. Требуется оценить неизвестное средне квадратическое отклонениепомощью доверительного интервала, покрывающего параметрс заданной надежностью, если имеется его точечная оценка. Доверительный интервал дляимеет вид:

,

где - выборочная оценка;(– точность оценки).

Величина табулирована в любом учебнике, следовательно, по заданнымипо таблице можно найти. Итак, вычислив по выборкеи найдя по таблице, получим искомый доверительный интервал, покрывающий неизвестное среднее квадратическое отклонение с заданной надежностью.

В нашем примере для ипо таблице (В.Е. Гмурман, «Введение в теорию вероятностей и математическую статистику», приложение 4) находим :

; .

Поясним смысл, который имеет заданная надежность . Из 100 выборок 95 определяют такие доверительные интервалы, в которых параметры (и) действительно заключен, и только в пяти выборках он может выйти за границы доверительного интервала.

Задача

Какова вероятность того, что наудачу взятая деталь с размерами из таблицы 1 окажется годной, если годными считаются детали размером от 72,20 до 72,60?

Решение

Искомую вероятность находим по формуле

;

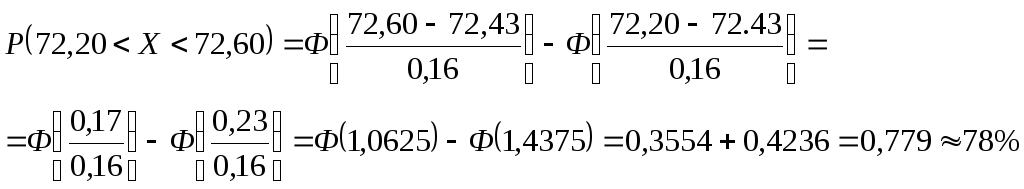
Полученный ответ нужно понимать так: из каждой сотни случайно отобранных деталей 78 деталей будут считаться годными.

Примечание: – функция Лапласа, значения которой приведены в таблице.