3. Нахождение оптимального плана выпуска продукции

Для определения оптимального решения исходной задачи х^* = (х, х, х). используем условия «дополняющей нежесткости»:

х (8u+17u – 670) = 0,

х (9u+15u – 504) = 0,

х (13u+9u – 530) = 0,

u (585 – 8х – 9х – 13х) = 0,

u (703 – 17х – 15х – 9х) = 0.

Подставим оптимальные значения переменных двойственной задачи в левые части ограничений двойственной задачи:

8u + 17u = 670

9u + 15u = 630 > 504

13u + 9u = 530

Таким образом, второе ограничение в точке оптимума является строгим неравенством (630 > 504). Поэтому из второго соотношения дополняющей нежесткости следует, что х(630 – 504) = 0 и значит х= 0.

Поскольку оптимальные значения переменных двойственной задачи положительны, то оба соотношения прямой задачи выполняются как равенства, т.е.

.

Так как , то для нахождения оптимальных значений оставшихся переменных прямой задачи достаточно решить систему уравнений:

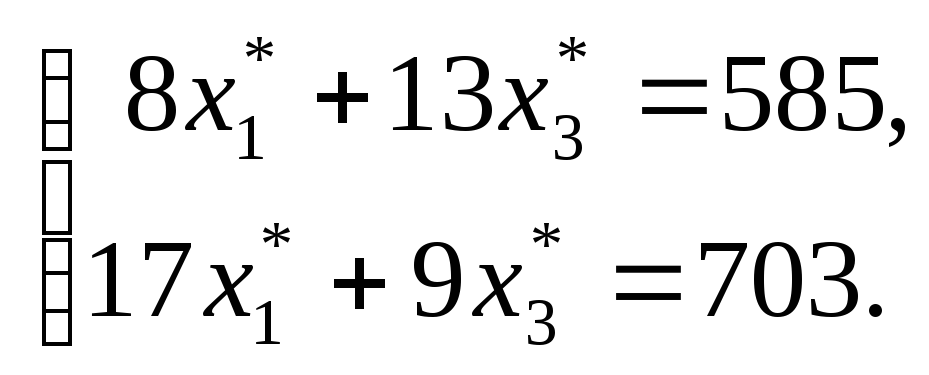
Ее решение: х₁ = 26, х₃ = 29 и следовательно, оптимальное решение прямой задачи таково: х^* = (26; 0; 29), а Z^* = 670×26 + 530×29 = 32790.

Так как оптимальные значения целевых функций обеих задач равны (Z^* = W^*), это означает, что обе задачи решены правильно.

Таким образом, в оптимальный план вошли первый и третий вид продукции. Должно быть выпущено 26 изделий первого вида и 29 изделий третьего вида. Суммарный доход от их продажи составит 32790 руб.

10