4. Экономическая интерпретация переменных и оптимального решения двойственной задачи

Двойственная задача к задаче фирмы интерпретируется как задача определения оптимальных оценок на ресурсы фирмы, ее переменные — как их оценки, а целевая функция — как суммарная стоимость ресурсов в этих оценках.

Оптимальная оценка ресурсного ограничения допускает такую экономическую интерпретацию: она характеризует предельную эффективность использования ресурса. Ее величина показывает, насколько возрастет оптимальное значение задачи, если объем данного ресурса увеличится на единицу.

Таким образом, включение дополнительной единицы сырья в процесс производства приведет к увеличению выручки на 1 тыс. руб., авключение дополнительной единицы оборудования в процесс производства приведет к увеличению выручки на 2 тыс. руб. Нулевая оценка труда говорит о том, что включение его дополнительной единицы не приведет к увеличению выручки. Это связано с тем, что труд в оптимальном плане выпуска недоиспользуется. Поскольку этот ресурс имеется в избытке, он имеет нулевую предельную эффективность.

Задача 2

Фирма производит три вида изделий, используя два вида ресурсов. Нормативы затрат ресурсов на единицу выпускаемой продукции, наличные объемы ресурсов и цены реализации продукции приведены в таблице.

Ресурсы	Нормативы затрат			Наличный объём
	Изделие 1	Изделие 2	Изделие 3
Сырьё (кг.)	8	9	13	585
Труд (чел./час)	17	15	9	703
Цена (руб.)	670	504	530

Задача фирмы состоит в том, чтобы определить программу выпуска, которая обеспечивает получение максимальной выручки от реализации готовой продукции.

Требуется:

1. Составить экономико-математическую модель расчета производственной программы и записать ее в виде задачи линейного программирования.

2. Построить двойственную задачу и найти графическим методом ее решение.

3. Используя условия «дополняющей нежесткости», найти оптимальный план выпуска продукции.

1. Построение математической модели

Пусть х_j – количество изделийj-го вида (j=), которое будет производиться фирмой. Тогда производственная программа (план) выпуска задается векторомх= (х₁,х₂,х₃). Для ее выполнения нужно затратить 8х₁+ 9х₂+ 13х₃кг сырья и 17х₁+ 15х₂+ 9х₃чел./час трудовых ресурсов, причем затраты не должны превосходить наличного объема этих ресурсов.

Выручка Z(х)от продажи произведенной продукции вычисляется по формуле

Z(х)= 670х₁+ 504х₂+ 530х₃

Задача фирмы состоит в получении максимальной выручки от продажи произведенной продукции, следовательно, Zявляется целевой функцией. Таким образом, на множестве всех допустимых плановх= (х₁,х₂,х₃) ищется план, на котором достигает максимума целевая функцияZ, т.е. математическая модель задачи имеет вид:

Z = 670х₁ + 504х₂ + 530х₃ max

8х₁ + 9х₂ + 13х₃ 585,

17х₁ + 15х₂ + 9х₃ 703,

х_j 0, j = .

2. Построение двойственной задачи и ее решение графическим методом

Пусть u₁ – двойственная оценка ограничения по сырью, а u₂ – двойственная оценка ограничения по труду.

u₁ ↔ 8х₁ + 9х₂ + 13х₃ 585,

u₂ ↔ 17х₁ + 15х₂ + 9х₃ 703,

Тогда двойственная задача к прямой (исходной) задаче будет иметь вид:

W = 585u₁ + 703u₂ min

x₁ ↔ 8u₁ + 17u₂ 670 (1)

x₂ ↔ 9u₁ + 15u₂ 504 (2)

x₃ ↔ 13u₁ + 9u₂ 530 (3)

u₁ 0, u₂ 0

Решим эту задачу графическим методом. Для этого построим граничные прямые полуплоскостей, задаваемых ее ограничениями (1) – (3):

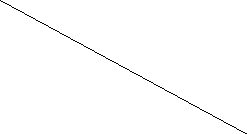
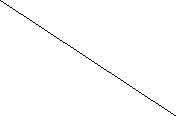
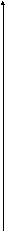1) 8u1+17u2 = 670 u1 0 83,75 u2 39,4 0	2) 9u1 + 15u2 = 504 u1 0 56 u2 33,6 0
3) 13u1 + 9u2 = 530 u1 0 40,76 u2 58,8 0

u₂

А

58,8

39,4

В

33,6

7,03

С

5,85 40,76 56 83,75 u₁

(3) (1)

(2)

Рис. 1. Графическое решение двойственной задачи

Ни одно из неравенств (1) – (3) не содержит начала координат – точки (0, 0). Поэтому область допустимых решений (ОДР) лежит справа от ломаной линии, образованной граничными прямыми (1), (2), (3) и осями координат. Опа представляет собой бесконечный многоугольник с вершинами A, B и C.

Чтобы градиент целевой функции можно было представить на графике, уменьшим его компоненты в 100 раз, т.е. построим вектор = (5,85; 7,03). Проведем перпендикулярно градиенту линию нулевого уровня целевой функции, проходящую через начало координат. Затем переместим ее параллельно самой себе в направлении возрастания градиента.

Так как решается задача на минимум, то первая точка, в которой перемещаемая линия уровня коснется ОДР, будет точкой оптимума. Этой точкой, как видно из чертежа, является точка В. Она находится на пересечении 1-й и 3-й граничной прямой. Поэтому для нахождения ее координат нужно решить следующую систему уравнений

8u₁+17u₂ = 670

13u₁+9u₂ = 530

Решив эту систему, получим оптимальное решение двойственной задачи:

u= 20, u= 30, W^* = 585×20 + 70×30 = 32790.

Это решение задает оптимальные двойственные оценки ресурсов для фирмы, т.е. стоимостная оценка 1 кг сырья составит 20 руб., а 1 чел.-час. трудовых ресурсов – 30 руб. Общая стоимостная оценка затрат на ресурсы составит 32790 руб.