Cadence / DSD11-1 / Chapter5

5.Активные фильтры и гираторы

5.1 Активные фильтры

Идеальный частотный фильтр – это устройство, имеющее передаточную характеристику, постоянную и отличную от нуля, в определенном диапазоне частот (называется полосой пропускания), и нулевую в остальном диапазоне ( называется полосой подавления).

Простейшие RL и RC фильтры низких (рис.5.1а) и высоких (рис.5.1б) частот имеют пологие характеристики спада амплитудно-частотной характеристики – 6 дБ/октаву. Повышение крутизны спада АЧХ требует применения фильтров более высокого порядка, однако, простое каскадное соединение элементарных звеньев обладает следующими недостатками:

• не позволяет получить идеальную прямоугольную характеристику, из-за невозможности обеспечить крутой перегиб АЧХ;

• в случае применения катушек индуктивности приводит к сложности интегрального изготовления фильтра, а интегральные катушки индуктивности обладают плохой добротностью;

• входное сопротивление каждого звена служит существенной нагрузкой для предыдущего.

Перечисленные недостатки привели к созданию фильтров с усилителем, позволяющим синтезировать характеристику RLC фильтра без катушек индуктивности. Электрическая схема активного фильтра нижних частот приведена на рис.5.2а. Передаточная функция такого фильтра имеет вид:

(5.1)

Чтобы получить фильтр верхних частот, необходимо в выражении (5.1) величину p заменить на 1/p. В схеме достаточно поменять местами R₁ и С, как это показано на рис.5.б. Другой способ создания фильтров нижних и верхних частот - использование частотно зависимой обратной связи.

Построенный на таком принципе фильтр нижних частот показан на рис.5.2а. Его передаточная характеристика имеет вид:

(5.3)

Для расчета схемы необходимо задать частоту среза , коэффициент усиления по напряжению и емкость конденсатора . Тогда соотношения для резисторов составляют:

и (5.4)

Для фильтра верхних частот (рис.5.3б) передаточная функция и соотношения для резисторов имеют вид:

, и (5.5)

Приведенные выражения для передаточных функций (5.1), (5.3) и (5.5), справедливы для частот, при которых модуль собственного коэффициента усиления операционного усилителя не сильно зависит от частоты. Для высоких частот изменяется со скоростью 6 дб/октаву и это свойство может быть использовано для реализации фильтра нижних частот при высоких частотах среза. Передаточная функция такого устройства имеет вид:

(5.6)

Учитывая приведенные соотношения, электрическая схема фильтра нижних частот имеет вид, показанный на рис.5.4.

5.2 Преобразователи отрицательного полного

сопротивления и гираторы

Преобразователь отрицательного полного сопротивления (рис.5.5) преобразует полное сопротивление Z1 в ему противоположное по знаку. Легко видеть, что в результате приращения напряжения на входе, приращение входного тока составит:

при коэффициенте обратной связи равном 1, получим

.

Тогда сопротивление устройства со стороны входа будет равно:

(5.8)

Как было отмечено выше, реализация индуктивностей в фильтрах применяемых в ИМС, представляет значительную проблемму. Таким образом преобразователь отрицательного полного сопротивления превращает конденсатор Z=1/jC в катушку индуктивности –Z=j/C, так как генерируемый ток запаздывает относительно приложенного напряжения. Однако полное сопротивление имеет неправильную

частотную зависимость (при возрастании частоты Z – убывает). В связи с этим актуальными являются гираторы - устройства преобразующее емкость в индуктивность.

На рис.5.6 приведена электрическая схема гиратора Легко видеть, что сопротивление со стороны входа составит:

(5.9)

Если , то где .

5.3 Фильтры с частотно-зависимой обратной связью.

5.3а Реализация фильтров низких и высоких частот второго порядка.

В общем виде передаточная функция фильтра НЧ второго порядка

Как отмечалось ранее оптимальные передаточные функции второго и более высокого порядка характеризуются наличием комплексно-сопряженных полюсов. Такие функции могут быть реализованы с помощью пассивных LRC – цепей(рис. ).

С учетом (1) получим

a1=1.414 в1=1,0

Можно использовать аналог L – гиратор. Однако такое схемное решение дорогостоящее. Заданную передаточную функцию можно реализовать с помощью сложной отрицательной обратной связи.

Передаточная характеристика активного фильтра нижних частот, изображенного на рис.5.7, имеет вид:

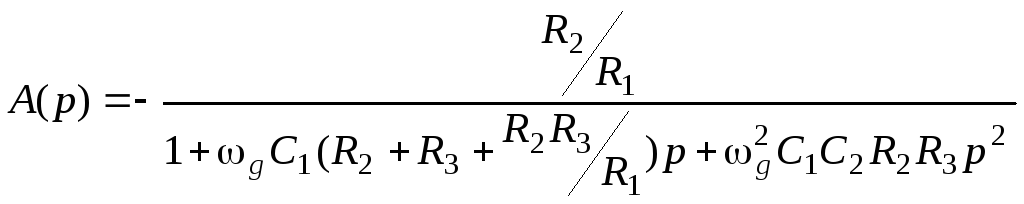
Для расчета фильтра необходимо задать значения емкостей конденсаторов и вычислить номиналы резисторов. Исходя из этого, имеем:

(5.10)

где , , .

Для того чтобы значение сопротивления R₂ ,было действительным необходимо выполнение условия:

(5.11)

Активный фильтр может быть также построен на основе операционного усилителя с положительной обратной связью. Отрицательная обратная связь (рис.5.8), сформированная с помощью делителя напряжения, обеспечивает коэффициент усиления . Положительная обратная связь по переменному току создается с помощью емкости С₂. Передаточная функция фильтра описывается следующим выражением:

(5.12)

Расчет фильтра существенно упрощается, если задать некоторые дополнительные ограничения. Например, можно положить коэффициент усиления по постоянному току равным единице, т.е. . При этом операционный усилитель преобразуется в повторитель со 100% обратной связью. Тогда передаточная функция существенно упрощается и принимает следующий вид:

(5.12а)

Считая, что емкости конденсаторов С₁ и С₂ заданы получим:

(5.13)

где ,

Для того чтобы значения R₁ и R₂ были действительными необходимо выполнение условия:

(5.14)

5.4. Пример реализации фильтра третьего порядка.

Если амплитудная характеристика фильтра недостаточно крутая то, как правило, используют фильтры более высокого порядка. Для этого последовательно соединяют звенья рассмотренные в разделе

5.1. Передаточные характеристики фильтров при этом перемножаются.

На практике существуют различные соображения о последовательности соединения звеньев. Так например, с точки зрения уменьшения вероятности перегрузки схемы лучше располагать звенья фильтров в порядке возрастания частоты среза и фильтр с наименьшей частотой поместить на вход.

Другая точка зрения на порядок расположения звеньев фильтра связана с обеспечением минимального уровня шумов. В этом случае последовательность подключения должна быть обратной, поскольку наличие звена с наименьшей частотой среза в конце цепочки ослабляет шумы предыдущих каскадов.

На рисунке 5.9 показан пример фильтра низкой частоты третьего порядка, коэффициент передачи которого равен единице с частотой среза . Задав значение емкости конденсатора С₁₁=100 пФ для R₁₁ получим:

Для второго каскада фильтра зададим величину емкости С₂₂=100пФ, тогда условие для определения емкости конденсатора С₂₁ в соответствии с (5.14) имеет вид:

Выбрав ближайший номинал С₂₁=47 пФ из стандартного ряда для R₂₁, в соответствии с(5.13), имеем:

Следует отметить, что можно несколько упростить схему, исключив первый операционный усилитель. При этом перед фильтром второго порядка будет включен простой пассивный фильтр нижних частот. Из-за взаимной нагрузки каскадов его

параметры необходимо рассчитать снова, что является непростой задачей.