1.2.5. Системы восстановления несущей.

В спектре сигналов, используемых в цифровых спутниковых системах связи, не содержится несущей частоты, поэтому когерентное колебание выделяют из принимаемого сигнала посредством некоторого нелинейного преобразования и последующей фильтрацией.

Наиболее общим подходом, позволяющим синтезировать устройство восстановления несущей из принимаемого сигнала, является использование критерия максимального правдоподобия. Восстановление несущего колебания можно рассматривать как задачу оптимального оценивания фазы сигнала, пораженного помехой (на интервале длительности символа Т_с):

.

Здесь n(t) - белый гауссовский шум с односторонней спектральной плотностью N₀. Фаза сигнала j_i в процессе модуляции принимает равновероятно одно из возможных значений ,

a_i = 0, ... , M - 1; q₀ - начальная фаза, подлежащая оценке.

Максимально правдоподобная гипотеза формируется с учетом возможных гипотез о посылаемых образцах сигнала

.

При оценке начальной фазы q₀ выбирают такое ее значение, которое доставляет максимум плотности вероятности

.

Поскольку начальная фаза q₀ принимает равновероятно все возможные значения в интервале 0 ... 2p, а плотность p(x) не зависит от q₀, максимуму условной плотности p(q₀ /x) соответствует максимум апостериорного распределения p(x/q₀). С учетом всех возможных гипотез посылки сигнала с фазами j_i можно записать, что

,

а условное распределение при фиксированной фазе j_i

.

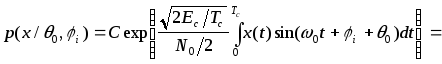
Здесь

,

-

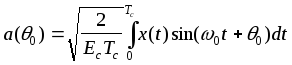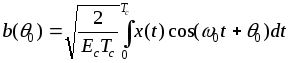выходы когерентных согласованных фильтров с квадратурными опорными колебаниями. Максимально правдоподобная оценка величины q₀ является решением уравнения

,

которое обращает в максимум выражение для p(x/q₀,j_i).

Для сигналов ФМ-4 с учетом того, что фаза j_i принимает четыре возможных значения 0, p/2, p, 3p/2, можно записать:

,

а уравнение для отыскания оценки

.

Поскольку оптимальная оценка a(q) и b(q) обычно заменяется фильтрацией, а th x » sgn x при x >>1, схема квазиоптимальной схемы восстановления несущей будет иметь вид, как на следующем рисунке. Она представляет собой схему Костаса.

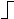
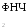
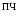
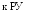
Рис. 12. Схема Костаса.

1.2.6. Тактовая синхронизация.

Система тактовой синхронизации (СТС) предназначена для выделения колебаний тактовой частоты, период которой определяет границы посылок передаваемых дискретных сигналов. Относительно этих границ выбирают момент взятия отсчета в РУ демодулятора.

В спектре случайного цифрового сигнала, как правило, не содержится компонента с тактовой частотой, поэтому ее приходится формировать из принятого сигнала путем некоторого нелинейного преобразования. Известны оптимальные структуры СТС, однако из-за сложности и некоторых упрощающих предпосылок при их синтезе они фактического применения не нашли.

На практике часто используют следующую структуру:

Рис. 13. Схема тактовой синхронизации.

Здесь Ф - фильтр, ВФ - схема выделения фронтов. Имеется большое многообразие схем выделения фронтов, большинство из которых формируют импульс при каждом переходе принятого цифрового сигнала через ноль. Схемы фильтрации в СТС могут быть как пассивными на полосовых фильтрах, так и активными на основе ФАП.