1.2.2. Спектральная характеристика сигнала.

Представление модулированных сигналов в виде суммы квадратурных составляющих удобно также для оценки их спектральных свойств. Симметричный радиочастотный спектр каждой составляющей с центральной частотой w₀ определяется односторонним спектром модулирующего сигнала I(t) либо Q(t), а энергетический спектр результирующего сигнала равен сумме спектров квадратурных составляющих. Энергетический спектр низкочастотного модулирующего сигнала определяют как преобразование Фурье его функции автокорреляции B(t):

.

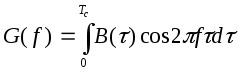Вычисление B(t) производят с учетом формы элементарных модулирующих сигналов p(t) и q(t). При этом предполагается, что информационные символы a и b в каналах независимы и равновероятны. Найденные таким образом функции энергетического спектра для ФМ-4 и СФМ-4 имеют вид:

.

Здесь f - отклонение текущей частоты спектра от центральной частоты f₀ = w₀/2p.

На рисунке 6 показана зависимость нормированного энергетического спектра G(f)/G₀(0) от нормированной расстройки fT для ФМ-4 (СФМ-4). Главный лепесток спектра ФМ-4 (СФМ-4) содержит 90.5% всей мощности сигнала. Первые нулевые значения расположены на расстоянии 0.5/T от несущей. Максимум первого бокового лепестка спектра на 13.5 дБ меньше главного максимума.

При смещенной ФМ-4 энергетический спектр по сравнению с ФМ-4 не изменяется. Спектр ФМ-2 вдвое шире спектра ФМ-4 при той же скорости модуляции V = 1/Т.

Для системы связи «Банкир» была выбрана смещенная (офсетная) четырехпозиционная фазовая модуляция, что, исходя из вышесказанного, во многих отношениях является оптимальным.

Рис. 6. Энергетический спектр сигналов ФМ-2 и ФМ-4.

1.2.3. Сравнение помехоустойчивости сигналов.

При равновероятных передаваемых сигналах средняя вероятность ошибки воспроизведения сигнала на выходе приемника

,

где - вероятность ошибки при передаче сигналаs_i,

i = 1, 2, 3, ... M - 1.

Согласно теории потенциальной помехоустойчивости минимум P₀ достигается при оптимальном приеме, основанном на вычислении апостериорных вероятностей P(S_i / Z), Z = f(Z,N) - принимаемый сигнал с помехой. Алгоритм работы оптимального приемника М - позиционных сигналов имеет вид:

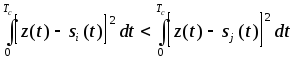
i, j = 0, 1, 2, ... , M - 1; i ¹ j.

При выполнении неравенства приемник выносит решение о приеме

сигнала S_i. Он содержит М каналов обработки, в каждом из которых вычисляется квадрат расстояния

и решающее устройство, которое выносит решение о принятом сигнале по наименьшему из расстояний.

Для сигналов с одинаковыми энергиями алгоритм приема преобразуется к виду:

.

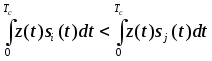В каналах обработки такого приемника содержатся корреляторы, поэтому прием называется корреляционным.

Работу приемника можно представить геометрически. Сигналы S₀, ... , S_{M - 1} отображаются сигнальными точками. Пространство сигналов разбивается на М областей. Границами сигнальных областей служат плоскости, равноотстоящие от сигнальных точек, соответствующих парам сигналов S_i и S_j. Оптимальному приему соответствует такое разбиение пространства на области сигналов, при котором достигается минимум средней вероятности ошибок P₀. Ошибка при передаче сигнала происходит, когда вектор принимаемого сигнала с помехой выходит за пределы области сигнала. Оптимальным выбором расположения сигнальных точек достигается минимум средней вероятности ошибки P₀.

Сигнал ФМ-4 представляет собой два двоичных сигнала, передаваемых одновременно, то есть в каждый момент приема необходимо выбрать один из четырех вариантов. Пространство сигналов ФМ-4 можно изобразить так:

Рис. 7. Пространство сигналов ФМ-4.

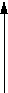
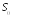
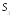
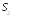
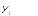
Здесь в качестве ортов возьмем векторы, соответствующие колебаниям с единичной энергией

и

,

,

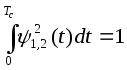а каждый сигнал изображается на плоскости вектором.

Разделение сигналов ФМ-4 в соответствии с описанным алгоритмом можно упростить. Как видно из рисунка, для решения о том, в какой из четырех областей находится вектор, достаточно определить его проекции на орты y₁ и y₂, решение можно вынести по знакам проекций. Если, например,

и ,

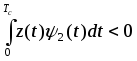то можно принять решение о приеме сигнала S₁.

Схема демодулятора такого приемника содержит два канала с опорными колебаниями cosw₀t и sinw₀t, интеграторами И и решающими устройствами РУ, в которых определяются полярности сигналов в каналах. Для работы этих устройств необходимы сигналы тактовой синхронизации ТС. Сигналы опорной несущей и ТС вырабатываются в специальных вспомогательных схемах демодулятора. В коммутаторе К происходит преобразование решений в квадратурных каналах в последовательности символов на выходе демодулятора. Простейшая структурная схема демодулятора ФМ-4:

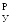
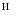
Рис. 8. Демодулятор ФМ-4.

При идеальной демодуляции полагают, что параметры принимаемого сигнала (временные границы посылок, значения частот и начальных фаз и др.) известны точно. В реальных условиях сведения о параметрах сигнала формируются при действии помех. Кроме того, в реальных трактах действуют дестабилизирующие факторы (нестабильности частот гетеродинов, скачки фазы, колебания уровней сигналов и др.), что увеличивает погрешность оценки параметров. Рекомендуемые теорией оптимального приема алгоритмы могут быть реализованы лишь приближенно. Влияние всех этих факторов увеличивает величину энергетических потерь. Допустим зависимость p = f(E_б/N₀) при идеальной демодуляции, определяемой потенциальной помехоустойчивостью, соответствует сплошной кривой на рисунке

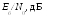
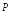
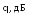
Рис. 9. К определению энергетических потерь.

Помехоустойчивость в реальных условиях будет хуже, и кривая на таком графике будет смещена вправо. На рисунке реальная кривая изображена пунктиром. Энергетические потери q показывают, насколько необходимо увеличить отношение сигнал / шум на входе реального демодулятора, чтобы вероятности ошибок остались прежними. Идеальные кривые помехоустойчивости удобно использовать для экспериментальной оценки того, насколько ухудшает то или иное устройство отношение сигнал / шум. Для такой оценки строят экспериментальную кривую достоверности и сравнивают ее с теоретической. При корректно проведенном эксперименте неизменная по форме кривая оказывается смещенной вправо, что позволяет оценить величину потерь.

На рисунке 10 приведены графики помехоустойчивости при идеальном приеме для разных сигналов.

Рис. 10. Графики помехоустойчивости при идеальном приеме.

Из графиков следует, что помехоустойчивость ФМ-4 такая же, как у ФМ-2. Действительно, ведь канал с ФМ-4 содержит два независимых канала ФМ-2 - следовательно для сигналов с этими видами модуляции вероятность ошибки будет одинакова.

В связи со всем вышесказанным в цифровых системах спутниковой связи широкое применение находит именно ФМ-4 двукратная фазовая модуляция сигналов. В том числе и в системе «Банкир» применяется именно этот вид модуляции, а именно - смещенная (офсетная, от английского offset - смещение) двукратная (ФМ-4) фазовая модуляция с относительным кодированием сигнала.