1.2. Теоретические сведения и обоснование функциональной схемы демодулятора.

1.2.1. Дискретные сигналы, методы модуляции.

Основная тенденция развития современных цифровых систем спутниковой связи - повышение помехоустойчивости и эффективности передачи сигналов. Решению этих задач способствует рациональный выбор сигналов, используемых для передачи сигналов по спутниковым каналам, методов их формирования и обработки на приеме. В современных системах связи широко применяют сигналы с фазовой модуляцией и когерентный прием. Наряду с двоичными применяются многопозиционные методы модуляции.

Коротко рассмотрим основные виды сигналов и методы их формирования. В общем виде колебание модулированной несущей с частотой w₀

s(t) = S(t)cos[w₀t - j(t)].

Здесь функции S(t) и j(t) определяют закон модуляции амплитуды и фазы несущей. Сигнал M- позиционной фазовой модуляции (ФМ-М) на интервале одного символа 0...Т_с

s_i(t) = S₀cos(w₀t - j_i).

Дискретные значения фазы сигнала j_i = 2p a_i/М, М - число возможных сигналов, М-ичные символы a_i выбираются из множества {0,1,2,...,М - 1}. Обычно М = 2^k, k = 1,2,3 ... Тогда каждый М-ичный символ a_i соответствует набору из k = log₂М двоичных информационных символов u, а его длительность Т_с = Т log₂М, где Т - длительность двоичного сигнала.

Энергия ФМ - сигнала постоянна и составляет

.

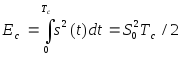Она может быть выражена через энергию Е_б, затрачиваемую на передачу одной двоичной единицы (бита) как Е_с = Е_бlog₂М. Длительность бита Т определяет скорость модуляции V = 1/Т в двоичных символах в секунду.

При М-2 получаем сигналы двоичной фазовой модуляции (ФМ-2, Е_с = Е_б):

,

.

Сигналы с одинаковыми энергиями удобно характеризовать коэффициентом корреляции:

.

Сигналы ФМ-2 противоположны и коэффициент корреляции R₁₂ = -1.

Модулированный сигнал s(t) можно представить в виде суммы квадратурных составляющих:

.

Выражения в квадратных скобках определяются видом передаваемой информации и модулируют ортогональные несущие cosw₀t и sinw₀t. Обозначим

,

.

Вид модулирующих функций I(t) и Q(t) задает метод модуляции и задает свойства сигналов. Представим их в виде

,

,

где a_n, b_n - информационные символы, p(t) и q(t) - элементарные модулирующие сигналы в квадратурных каналах. Последовательности символов a и b получают расщеплением исходной информационной последовательности на четные и нечетные символы. Символы a и b могут быть как двоичными, так и многоуровневыми.

Обычно модулирующие сигналы выбирают такими, чтобы при последовательной передаче в каждом из квадратурных каналов они не перекрывались во времени. Это условие выполняется, если длительность каждого сигнала (p(t) или q(t)) равна Т_с. В этом случае имеет место модуляция полным откликом и в формируемых в модуляторе сигналах отсутствует межсимвольная интерференция. Такие методы достаточно просты и их широко используют на практике. При модуляции частичным откликом длительность сигналов p(t) и q(t) превышает Т_с, допускается взаимное перекрытие сигналов и межсимвольная интерференция. Процесс обработки и демодуляции при этом усложняется, но такие сигналы обладают лучшими спектральными свойствами.

Для сигналов с постоянной огибающей должно выполняться условие:

.

Такому условию удовлетворяют элементарные модулирующие сигналы в виде прямоугольных импульсов:

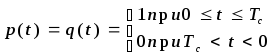
при этом двоичные информационные символы полагаются равными a_n = ±1 и b_n = ±1. В этом случае получаем сигналы двукратной ФМ. На интервале длительностью Т_с = 2Т четыре возможные комбинации символов a и b задают следующие варианты сигналов четырехпозиционной ФМ:

,

,

,

.

Они образуют биортогональный комплекс сигналов, так как сигнал s₀(t) = - s₂(t) и s₁(t) = - s₃(t), а сигналы s₀(t) и s₁(t), s₂(t) и s₃(t) взаимно ортогональны (R₀₁ = R₀₃ = 0).

Представление сигналов в виде суммы квадратурных составляющих определяет простой способ их получения в модуляторе. В частности, сигналы ФМ-4 можно получить как сумму двух сигналов ФМ-2, несущие колебания которых отличаются по фазе на p/2:

Простейшая схема такого модулятора показана на рис. 4.

Двоичная последовательность информационных символов u в коммутаторе К разделяется на последовательности a и b которые модулируют квадратурные несущие cosw₀t и sinw₀t. Длительность каждого символа u равна Т, а длительности a и b равны Т_с = 2Т . Сигналы ФМ-2 квадратурных каналов складываются, образуя четырехфазный канал ФМ-4.

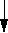
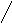
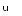
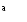
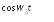
Рис. 4. Структурная схема модулятора ФМ-4.

При одновременной смене символов в каждом из квадратурных каналов модулятора ФМ-4 происходит скачок фазы на p. Прохождение ФМ сигнала через полосовые фильтры тракта сопровождается изменениями огибающей сигнала в моменты, соответствующие скачкам фазы. Скачки на p вызывают провалы огибающей до нуля. Такая паразитная модуляция сигнала нежелательна. Исключить скачки фазы на p возможно, если разнести во времени моменты смены фаз в квадратурных каналах. Обычно модулирующие сигналы в одном из каналов смещают на величину Т_с/2.

Например, выбирая элементарные модулирующие сигналы в виде:

,

,

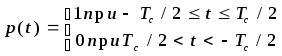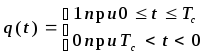и полагая что a_n = ±1 и b_n = ±1, получим сигналы смещенной (или иначе офсетной) ФМ-4. Формы элементарных модулирующих сигналов при СФМ-4 показаны на рисунке 5.

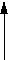
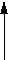
Рис. 5. Формы элементарных модулирующих сигналов при модуляции СФМ-4.

Модулятор офсетной ФМ-4 отличается от ФМ-4 наличием в одном из квадратурных каналов задержки на Т_с/2. На рисунке элемент задержки изображен пунктиром.

Опорная несущая, необходимая для когерентного приема в демодуляторе, выделяется, как правило, из принимаемого сигнала. При этом возникает неоднозначность фазы, когда возможно выделение с ошибкой, кратной 2p/М.

Передача ФМ в каналах с неоднозначностью требует применения специальных мер. Чаще других используют относительное кодирование информации по правилу

,

где u - символы на входе кодера, u - символы на его выходе, а - задержанные на такт выходные символы. Другими словами, в сигнале с относительным кодированием, собственно исходная цифровая информация заключается не в значении символа, а в изменении его значения. Рассмотрим, для примера, сигнал ФМ-2, предварительно подвергнутый относительному кодированию. При перескоке фазы наp в таком сигнале возникает всего две ошибки. В то же время в не кодированном сигнале вся двоичная последовательность после перескока фазы окажется инвертированной.

Символы относительного кода подают на модулятор ФМ, получая на выходе сигнал относительной фазовой модуляции. В демодуляторе производится обратное преобразование.