3.2.2. Общее описание алгоритма коррекции фрагмента.

С использованием вышеперечисленных понятий, алгоритм имеет следующий вид:

1. Определение типа слоя металлизации (горизонтальный слой или вертикальный).

2. Поиск пустых областей во фрагменте топологии.

3. Разбиение каждой пустой области на прямоугольные области. Тип разбиения зависит от типа слоя металлизации.

4. Определение числа лжепроводников, которое способна вместить каждая прямоугольная область.

5. Равномерное заполнение лжепроводниками прямоугольной области.

6. Дополнительная коррекция фрагмента.

Ниже подробно рассмотрен каждый шаг алгоритма.

3.2.3. Детальное описание алгоритма.

Если весь слой заполняется лжепроводниками одного типа, то строго говоря, Шаг 1 необходимо выполнить один раз перед началом коррекции всех фрагментов слоя. Однако если желательно, чтобы лжепроводники имели ориентацию в соответствии с типом корректируемого фрагмента, а не с типом всего слоя, можно «подсунуть» на первом шаге только данный фрагмент слоя. На этом шаге подсчитывается число горизонтально и вертикально направленных проводников.

Если число горизонтальных проводников превышает число вертикальных, то слой полагается горизонтальным; в противном случае слой вертикальный. В дальнейшем все пустые области заполняются лжепроводниками в соответствии с типом слоя.

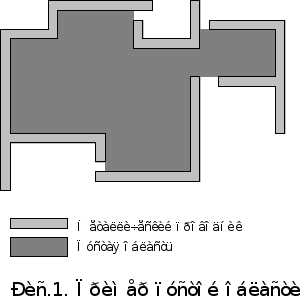
Во время выполнения Шага 2 просматривается весь фрагмент слоя металлизации в целях поиска пустых областей. Так как проводники имеют либо вертикальное, либо горизонтальное направление, то каждая пустая область представляет собой сложную фигуру с прямыми углами. На рис.1 показан пример пустой области.

На Шаге 3 метод разбиения пустой области зависит от типа слоя: для пустой области горизонтального слоя проводится тип разбиения «горизонтальная мозаика», для вертикального - тип «вертикальная мозаика». На рис.2 показаны оба типа разбиения пустой области из рис.1.

Разбиение «горизонтальная мозаика» выполняется следующим образом: в пустой области находится самый верхний левый угол, далее проводится поиск верхнего правого угла; таким образом определяется ширина прямоугольной области. Продвигаемся сверху вниз по сторонам прямоугольной области, пока не обнаружим угол на какой-либо стороне; по трем найденным углам определяем прямоугольную область. Затем эта операция повторяется для оставшейся части пустой области. Разбиение «вертикальная мозаика» проводится аналогично, но сначала определяется самый левый верхний угол, затем нижний левого угол, а третий угол ищется продвижением по верхней и нижней сторонах области слева направо.

Причина применения таких методов разбиения рассматривается ниже после описания алгоритма.

После разбиения пустой области Шагом 4 определяется число лжепроводников, способное разместится в каждой прямоугольной области. Пусть прямоугольная область имеет ширину Width и высоту Height. Тогда для горизонтального слоя число лжепроводников определяется по формуле

N = ,

а для вертикального слоя по формуле

N = ,

где операция [x] означает ближайшее целое, не превосходящее x (т.е. отбрасывание дробной части x).

Однако простое размещение лжепроводников на расстоянии m друг от друга может привести к тому, что в нижней части прямоугольной области горизонтального слоя и в правой части области вертикального слоя может остаться пустая область достаточно большого размера (см. рис. 3). В этом случае лжепроводники необходимо равномерно разместить в области. Равномерным называется такое размещение лжепроводников, при котором все расстояния между соседними лжепроводниками отличаются друг от друга не более, чем на 1. Равномерное размещение области выполняется Шагом 6 алгоритма. При этом используется следующий метод:

• определяется дополнительный зазор последним лжепроводником (последним лжепроводником для горизонтального слоя является самый нижний, а для вертикального - самый правый лжепроводник области) и краем прямоугольной области (нижней стороны области

  

  для горизонтального и правой стороны для вертикального слоя). Дополнительным зазором s называется расстояние между указанными объектами без (m+1).

• если число N лжепроводников больше, либо равно s, увеличить расстояния между первыми s проводниками на 1 (изменяется также расстояние между первым лжепроводником (верхним для горизонтального слоя и левым для вертикального) и соответствующим краем области). В результате расстояния между первыми s лжепроводниками и между последним лжепроводником и краем области будут равны (m+1), а для остальных - просто m (см. рис. 4).

• если число N лжепроводников меньше, чем s, то начинается последовательная раздвижка лжепроводников, начиная с первого. При этом после очередной раздвижки сравниваются расстояния между первым и последним лжепроводниками и их соответствующими краями области: если они отличаются не более, чем на 1, то процесс прекращается. Если после раздвижки всех лжепроводников указанное условие не выполняется, то процесс повторяется.

Дополнительная коррекция, проводимая на Шаге 7, необходима для устранения ситуаций, с которыми приведенный алгоритм справляется нежелательным образом. Ситуация, показанная на рис. 5, возникает, когда существует прямоугольная область в вертикальном слое высотой, равной минимальной длине проводника (аналогичная ситуация может возникнуть и для горизонтального слоя). В этом случае было бы желательней заменить все лжепроводники минимальной

длины на один лжепроводник горизонтальной ориентации. Такая замена легко обеспечивается, если не заполнять такие области лжепроводниками по типу слоя, а после коррекции всего слоя провести повторную коррекцию, заполняя оставшиеся пустоты лжепроводниками другой ориентации.

На рис.6 показан результат применения указанного метода к ситуации на рис. 5.

Опишем теперь причину, по которой для разбиения прямоугольной области применялись указанные выше методы. Для примера рассмотрим пустую область в горизонтальном слое (см рис. 7).

При разбиении этой области методом, отличным от метода «горизонтальная мозаика», может оказаться так, что прямоугольные области касаются друг друга боковыми сторонами, как показано, например, на рис. 8. Как видно из результатов равномерного заполнения данных областей лжепроводниками (рис. 9), расположение

последних может показаться несколько странным и нелогичным с точки зрения человеческой логики. Кроме того, попытка выровнить и соединить концы лжепроводников является достаточно трудоемким занятием. Разбиение области методами, указанными выше при описании алгоритма, автоматически исключает появление таких ситуаций.