Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

лекция 6 для лектора окончат

.pdf

Скачиваний:

Добавлен:

31.03.2015

Размер:

506.43 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

- 1 -

Лекция 6 Условный экстремум

П.1. Условный экстремум. Постановка задачи. Необходимые условия условного экстремума

(без использования метода неопределенных коэффициентов Лагранжа)

Рассмотрим функцию от переменных: ( ) Пусть известны m дополнительных условий

1( x1,..., xn m ) 0
					(*)
...........................					(*)

	( x ,..., x		) 0
	( x ,..., x	n m	) 0
m	1	n m
называемых условиями связи (	(		)	(	) – некоторые

функции ) .

Рассмотрим множество точек, координаты которых удовлетворяют условиям связи, обозначим это множество :

M (x1,..., xn m ) | 1(x1,..., xn m ) 0,..., m (x1,..., xn m ) 0 .

Определение.	Говорят, что функция f (x1,..., xn m ) имеет условный минимум
(максимум) при условиях связи (*) в точке M		(x0	,..., x0	n m	) , если существует
	0	1		n m
окрестность U (M0 )	точки , такая, что для любой точки , принадлежащей
множеству U (M0 ) , выполнено неравенство
	f (M ) f (M0 ).
	()

Пусть функции f (M ), 1(M ),..., m (M ) имеют непрерывные частные производные по всем переменным в некоторой окрестности рассматриваемой

точки	M	(x0	,..., x0	) . Составим матрицу из частных производных функций
	0	1	n m
(			) (	) в точке			M		(x0	,..., x0			) :
							0		1		n m
					1	...		1		...	1
					x1	...		xn 1		...

											xn m
				......			.........				....... .
					m			m			m
					m	...		m		...	m
					x	...		x		...	x
					1				n 1			n m

Пусть отличен от 0 хотя бы один из миноров этой матрицы – го порядка ( то есть ранг этой матрицы равен )

Пусть для определенности

		1	.........	1
		1		1
D( 1	,..., m )	xn 1		xn m
		xn 1		xn m
		........ .........		.......	0 .
D( xn 1	,..., xn m )	........ .........		.......	0 .
		m	.........	m
		xn 1	.........	xn m
		xn 1		xn m

- 2 -

Из теоремы о существовании и дифференцируемости неявных функций, определяемых системой уравнений, получаем, что существует окрестность точки M0 (x10 ,..., x0n m ) , в которой определены и дифференцируемы неявные функции:

xn 1 1 (x1,..., xn )

............................. ,

xn m m ( x1,..., xn )

определяемые системой уравнений (*).

1случай. Пусть функции 1,..., m могут быть выписаны явно. Тогда задача об условном экстремуме функции f при условиях связи (*) сводится к задаче об обычном экстремуме сложной функции

g(x1,..., xn ) f (x1,..., xn ,1(x1,..., xn ),....,m (x1,..., xn )) .

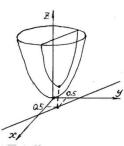
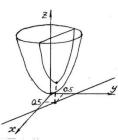
Пример 1. Рассмотрим задачу о поиске условного экстремума функции

при условии связи
Выразим переменную	из условия связи:		, подставим это
выражение в выражение для функции		:
	(	)
Далее ищем экстремум функции одной переменной, как обычно:
(	)	при
Найдем значение , используя условие связи:			Отсюда
получаем точку возможного условного экстремума: (			). Из рисунка видим,

что эта точка является точкой условного минимума функции ( ).

2 случай. Пусть не удается явно выписать выражения для функций 1,..., m . Пусть функции f (M ), 1(M ),..., m (M ) имеют непрерывные частные производные по всем переменным в некоторой окрестности рассматриваемой точки M0 (x10 ,..., x0n m ),

якобиан не равен 0 в точке . Следовательно, в некоторой окрестности точки существуют и дифференцируемы неявные функции

xn 1 1(x1,..., xn ),..., xn m m (x1,..., xn ) .
Предположим, что функция ( ) имеет условный экстремум в точке	при
условиях связи (*).

- 3 -

	Сложная функция g(x1,..., xn ) f (x1,..., xn ,1(x1,..., xn ),....,m (x1,..., xn )) имеет в точке
N	(x0 ,..., x0 ) безусловный экстремум. Вычислим первый дифференциал dg(N					) :
0	1	n			0
		n m	f
		dg(N0 )	f	dxi .
		dg(N0 )		dxi .
		i 1	x
		i 1	i
Точка		– точка экстремума, следовательно, ( )			Но dxn 1 ,..., dxn m -

дифференциалы неявных функций. Поэтому мы не можем сделать вывод о том,

что в точке	выполнено
				(		̅̅̅̅̅̅̅̅̅̅̅ ).
				(		̅̅̅̅̅̅̅̅̅̅̅ ).
Найдем дифференциалы зависимых переменных							Используем
условия связи (*):
		1 ( x1,..., xn m ) 0

			...........................

				( x ,..., x		) 0
				( x ,..., x	n m	) 0
		m		1	n m

Возьмем дифференциал от левых и правых частей этих равенств, используем инвариантность 1-го дифференциала:

1 dx ...
	x	1

	1
		......

	m
			dx ...

		1

1	dx		0
xn m	dx	n m	0
		n m

......			......(**)
m	dx		0
xn m	dx	n m	0
		n m

Мы предположили, что в окрестности точки M 0 якобиан					не равен 0:
	1	.........	1

	xn 1		xn m	0 .	(***)

	........ .........		.......
	m	.........	m
	xn 1		xn m

Рассмотрим систему (**) как систему из m уравнений относительно m неизвестных dxn 1 ,..., dxn m . Определитель этой системы совпадает с определителем в

левой части соотношения (***), он не равен 0, следовательно, решения системы (**) существуют. Найдем эти решения:

dxn 1 ... (dx1,..., dxn )

................................. .

dxn m ... (dx1,..., dxn )

Подставим эти выражения для дифференциалов dxn 1 ,..., dxn m в исследуемое уравнение:

n m f

dg x dxi 0 .

i 1 i

Получим уравнение вида

A1dx1 ... Andxn 0 ,

- 4 -

содержащее только дифференциалы независимых переменных				Левая
часть последнего равенства должна быть равна 0 для любых значений
дифференциалов	, следовательно, должны быть справедливы
равенств
	A1 0
	...........

	A 0
	n
Выписанная система из уравнений вместе с		условиями связи (*) и является
системой из (	) уравнений, позволяющей вычислить координаты
точки условного экстремума.
Таким образом, найдена система из (		) уравнений, представляющая собой
необходимое условие наличия условного экстремума в точке M			(x0 ,..., x0	n m	).
		0	1	n m

Пример 2. Решим задачу примера 1 вторым способом. Возьмем дифференциал от функции , приравняем его нулю. Приравняем также нулю первый дифференциал от условия связи. Допишем условие связи, получим систему

	{	.
Выразим из второго уравнения дифференциал				через
дифференциал	подставим в первое уравнение,
получим
	(	)
отсюда, учитывая условие связи, получим
		{
следовательно,		Точка (	) является точкой возможного
условного экстремума.

П.2. Необходимые условия условного экстремума в случае одного уравнения связи

(без использования метода неопределенных коэффициентов Лагранжа)

Рассмотрим задачу о поиске условного экстремума функции (

)

при условии связи

(

)

Справедлива теорема.

Теорема. Пусть в некоторой окрестности точки (

)

1) функции (

) (

) имеют непрерывные производные 1-го

порядка по всем переменным;

2) y (M0 ) 0 ;

3) M 0 - точка условного экстремума.

Тогда в точке (

(i 1, n) .

- 5 -

Доказательство. Из условий 1), 2) теоремы следует, что в некоторой

окрестности точки

(

) определена дифференцируемая неявная

функция y y(x1...xn ) , более того,

(i 1, n) .

(**)

Здесь производные в левой части берутся в точке

(

), производные в

правой части берутся в точке

(

Задача об условном экстремуме сводится к задаче об обычном экстремуме

сложной функции f (x1,..., xn , y(x1,..., xn )) g(x1,..., xn )

. Следовательно, все производные

функции в точке

(

)

должны быть равны нулю:

(

)

Отсюда получаем

, (в точке

(i 1, n) .

...........................

Используем соотношения (**):

............................

следовательно,

................................... .

▲

Пример. Опишем, как можно использовать утверждение

теоремы для поиска условного экстремума в задаче,

рассмотренной ранее. Имеем:

условие связи:

(

)

		- 6 -
Выпишем соотношение, доказанное в теореме:
			.
Дополним условием связи, получим систему			.
Дополним условием связи, получим систему
{	(	)	,
{			,

решаем, находим координаты точки возможного экстремума:

П.3. Условный экстремум. Необходимые условия условного экстремума

				Метод неопределенных коэффициентов Лагранжа
		Рассмотрим функцию			переменных: f (M ) f (x1,..., xn , xn 1,..., xn m ).
	Теорема.
	Пусть
1)	M	(x0	,..., x0	) является точкой условного экстремума для функции f (x ,..., x						)
	0	1	n m					1	n m
при условиях связи (*):
					1 ( x1,..., xn m ) 0
										(*)
					...........................					(*)

						( x ,..., x		) 0
						( x ,..., x	n m	) 0
					m	1	n m

2) функции f (x1,..., xn m ) , 1(x1,..., xn m ),..., m ( x1,..., xn m ) имеют непрерывные частные

производные первого порядка по всем переменным в некоторой окрестности точки

M 0 .

3) в точке

	1	.........	1

	xn 1		xn m

J	........ .........		.......	0 .
	m	.........	m
	xn 1		xn m

Тогда существуют числа

0 ,..., 0 такие, что точка (x0 ,..., x0

, 0

,..., 0 )

является

n m

стационарной точкой функции Лагранжа L(x1 ,..., xn m , 1

,..., m ) :

L(x1 ,..., xn m , 1

,..., m ) f (x1 ,..., xn m ) k k ( x1 ,..., xn m ) .

k 1

Здесь

– так называемые неопределенные множители Лагранжа.

Доказательство.

1) Вычислим производные функции

относительно переменных

L f

k , (

̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ ) .

k 1

(**)

- 7 -

Фиксируем коэффициенты 1 ,..., m такими, чтобы m производных функции

по переменным					(			̅̅̅̅̅̅̅̅̅̅̅ )	были равны нулю в точке M 0 :
	L		f		m	k			̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ )
					k			0 (		(***)
	x		x			x
		i		i	k 1		i

Система уравнений (***) является системой из m линейных уравнений

относительно неизвестных 1 ,..., m . Определитель этой совпадает с якобианом ,

но в силу условий теоремы					в точке	Следовательно, система (***)
является системой из			уравнений с квадратной невырожденной матрицей,
следовательно, она имеет единственное решение 1 ,..., m .
	Фиксируем это решение : 0			,..., 0 .
			1		m
2) Докажем, что, если			0 ,...,	m	0 , то есть равны нулю производные
		1	1		m
	(	̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ )	то производные функции и по другим переменным

равны нулю в точке M 0 .

Приведем некоторые дополнительные рассуждения, на которые сошлемся ниже. 1. Якобиан не равен нулю в точке , следовательно, в некоторой точке

окрестности точки M 0 существуют и дифференцируемы m неявных функций от переменных x1,..., xn :

xn 1 xn 1 (x1,..., xn )

................................. .

xn m xn m ( x1,..., xn )

2. M 0 - точка условного экстремума, следовательно, ее координаты удовлетворяют условиям связи

1 (M0 ) 0
...................

	(M		) 0
		0
m

3. M 0 - точка условного экстремума функции f

при условиях связи (*) ,

поэтому сложная функция

g(x1,..., xn ) f (x1,..., xn , xn 1(x1,..., xn ),..., xn m (x1,..., xn ))

имеет безусловный экстремум в точке (

) , и ее производные первого

порядка должны быть равны нулю в этой точке:

n m

x j

(i 1, n) .

(1)

j n 1

4. Производные от сложных функций

k (x1,..., xn , xn 1(x1,..., xn ),..., xn m (x1,..., xn )) (k 1, m)

по всем переменным

должны быть равны нулю, так как 1

0,...,m 0 :

n m

x j

, (i 1, n, k 1, m) .

(2)

j n 1

Вернемся к доказательству теоремы. Имеем:

- 8 -

̅̅̅̅̅)

{

(

выразим из соотношений (1)} =

k 1

n m

x j

j n 1

k 1

={ 1 ,..., m

выбраны так, что формула (***) верна. Выразим и подставим

производные

(

̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅) из соотношений (***)

n m

x j

k x

j n 1

k 1

={ bij

bij }=

i 1 j 1

j 1 i 1

n m

x j

k 1

j n 1

k 1

n m

x j

k 1

j n 1

n m

x j

так как

в силу соотношений (2).

j n 1

Таким образом, если в функции Лагранжа

положить

,...,

, где

коэффициенты

0 ,..., 0 являются решениями системы (***), то верны

соотношения

(****)

			{					0	,..., 0 такие, что точка
			{
Следовательно, действительно существуют числа
								1	m
(x0	,..., x0	, 0 ,..., 0 ) является стационарной точкой функции Лагранжа
1	n m	1	m
L(x1 ,..., xn m , 1 ,..., m ) :
								m
			L(x1 ,..., xn m , 1 ,..., m ) f (x1 ,..., xn m ) k k ( x1 ,..., xn m ) .
							k 1
									▲
Замечание. Система (****) является системой из									уравнений
относительно			переменных x0	,..., x0		, 0	,..., 0	. Эта система является
			1		n m	1	m

необходимым условием наличия условного экстремума в точке . Таким образом, вычислив все решения системы (***), найдем множество точек, «подозрительных» на наличие условного экстремума. Подтвердить наличие

- 9 -

условного экстремума в найденной точке можно, используя второй дифференциал функции Лагранжа ( смотри следующий пункт).

Часто заранее известно, например, исходя из геометрических соображений, что функция обладает условным экстремумом, следовательно, «подозрительная» точка действительно является точкой условного экстремума.

П.4. Условный экстремум. Достаточные условия наличия условного экстремума

(с использования метода неопределенных коэффициентов Лагранжа). Алгоритм решения задачи о поиске точек условного экстремума

Пусть точка (

) является стационарной точкой функции

Лагранжа

Ответ на вопрос о наличии условного экстремума в точке

(

) зависит от знака приращения

в точке

Имеем:

(

)

(

)

(

)

(

)

( ∑

∑

)

( ∑

∑

)

Здесь

, т.к.

– стационарная точка функции Для независимых

переменных

верно, что

Для зависимых

переменных верны равенства:

∑

(

) Найдем

выражения для дифференциалов

(

) используя условия

связи, подставим их в выражение для

Окончательно получим

(

), где

– квадратичная форма.

Аналогично тому, как это было сделано в случае безусловного экстремума, можно показать, что, если квадратичная форма является положительно (отрицательно) определенной, то функция имеет условный минимум (максимум) в точке

Рассмотрим алгоритм решения задачи поиска точек условного экстремума

функции (	) при условиях связи
	1( x1,..., xn m ) 0

	...........................

		(x ,..., x		) 0
		(x ,..., x	n m	) 0
	m	1	n m

1. Составляем функцию Лагранжа

L(x1 ,..., xn m , 1 ,..., m ) f (x1 ,..., xn m ) k k ( x1 ,..., xn m )

k 1

		- 10 -
Находим стационарные точки (			) ( вообще говоря, их может
быть несколько).
2. Строим для каждой стационарной точки функцию
(	)	(	)
Вычислим для этой функции второй дифференциал, который является
квадратичной формой переменных			(	)

3. Возьмем дифференциалы от левых и правых частей уравнений, входящих в систему (*), получим систему вида

{ .

Разрешим эту систему относительно дифференциалов зависимых переменных

	. Это можно сделать, так как определитель этой системы
совпадает с якобианом который по предположению не равен нулю.
	Подставим полученные выражения для дифференциалов	в
выражение для квадратичной формы . Получим квадратичную форму
(	) Исследуем ее на знакоопределенность. Если она является

положительно (отрицательно) определенной, то соответствующая стационарная точка является точкой минимума (максимума). Если же квадратичная форма не является знакоопределенной, то условного экстремума в соответствующей точке нет.

Пример. Рассмотрим задачу о поиске условного экстремума, решаемую выше:

( )		условие связи
Строим функцию Лагранжа:
	(				)
Ищем стационарные точки:

			,
	{
получим				Подставим в выражение для функции значение
и вычислим второй дифференциал

эта квадратичная форма является положительно определенной, следовательно,

точка	(	) является точкой условного минимума.
Рассмотрим еще один пример.
Пример. Найдем условный экстремум функции			условии
связи	x2 y2 9 0.
Составим функцию Лагранжа:
		L 6 5x 4 y (x2 y2 9).

Ищем стационарные точки:

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.03.20151.88 Mб28Лекция 4 микроэлектроника.doc
#
31.03.201553.26 Кб12ЛЕКЦИЯ 4 по ИЭ.docx
#
31.03.201575.78 Кб10ЛЕКЦИЯ 4 по ИЭУ.doc
#
31.03.2015233.98 Кб27Лекция 5 микроэлектроника.doc
#
31.03.2015165.38 Кб18ЛЕКЦИЯ 5 по ИЭУ.doc
#
31.03.2015506.43 Кб4лекция 6 для лектора окончат.pdf
#
31.03.2015805.38 Кб27Лекция 6 микроэлектроника.doc
#
31.03.201567.07 Кб17ЛЕКЦИЯ 6 по ИЭ.doc
#
31.03.20151.44 Mб27Лекция 7 микроэлектроника.doc
#
31.03.201590.62 Кб10ЛЕКЦИЯ 7 по ИЭ.doc
#
31.03.2015107.01 Кб6ЛЕКЦИЯ 7 по ИЭУ.doc