Petri EC signal deconvolution

defect. Furthermore, it is unclear how to select EC signal features that account for the combined effect of an array of cracks.

8. Lissajous pattern phase-angle rotations can arise when artifacts such as magnetite or copper deposits interfere with the eddy currents. For example, laboratory experiments have demonstrated that the presence of a copper foil wrapped around a tube can produce a 90 8C phase angle shift for a machined notch. Since the phase angle is related to crack depth and is an important signal feature used for ANN analyses, these distortions can severely affect ANN results. The EC deconvolution technique, by itself, cannot correct this error.

In spite of these potential complications, which would make it difficult to automate the deconvolution process, the technique gives promising results when used to predict tube burst pressures, as is illustrated in the following section.

5.EXAMPLE NEURAL NETWORK ANALYSIS OF EDDY CURRENT SIGNALS

Instead of characterizing and sizing individual tubing defects—a very difficult task—predicting the failure pressure of the tubes may be a more successful way to assess tube integrity. Eddy current bobbin probes respond to the overall extent of cracking in a tube, so EC signals should contain information relevant to tubing burst pressure. Artificial neural networks offer a way to relate EC results to burst pressure. The key to this problem, however, is to identify the important discriminating features of the EC signals to be used as input to the ANNs. In the example presented here, it is shown how the Gaussian deconvolution technique can improve the ANN analysis of steam generator tube eddy current signals.

5.1. Burst Pressure Data Set

Laboratory data were provided by the U.S. Nuclear Regulatory Commission as part of its ongoing steam generator tube integrity program at Argonne National Laboratory.(44) The data set included, along with the EC readings, measurements of the pressure required to rupture the tubes at room temperature. A large number of tubes were included, but only a few were suitable for the ANN study. Some tubes were rejected because they developed crack openings during burst pressure testing that allowed substantial leakage without rupture. Other tubes were dismissed because of a lack of complete calibration information. For these reasons, the data set used

in this Argonne ANN project consisted of only fourteen tubes.

The 7/8-inch outside-diameter (OD) Alloy 600 tubes were fit with collars along their axes to simulate various tube support plate configurations and were packed with simulated steam generator sludge. The tubes were exposed to an aggressive environment in the experiment facility to promote accelerated cracking. In most cases, the tubes developed cracks with complete penetration through the tube wall at the collars. Bobbin probes were used to collect EC signals through the cracked regions. Afterward, the tubes were removed from their collars, were burst-pressure tested, and were destructively examined. The burst pressure tests were performed at room temperature using an air-driven differential piston water pump. The reported burst pressures were normalized to account for differing roomtemperature flow stresses of the Alloy 600 lots, where the flow stress is defined as the average of the yield and ultimate tensile strengths.

All tube cracks originated on the outer (OD) tube wall and were, in general, oriented axially along the tube, which is typical of stress corrosion cracking in operating steam generators.(2,3) The crack morphologies ranged from single axial cracks to interconnected networks of small cracks. These various geometries would complicate the description of the cracking by a single measure, such as “crack length” or “crack depth.” Therefore, using eddy current signals to characterize these crack descriptions would not likely be successful. Instead, eddy current measurements are sensitive to the overall crack geometry—including length, depth, volume, and extent of branching. The combination of these geometric features directly affects the structural integrity (i.e., the burst pressure) of the tube. Thus, the use of eddy current signals to characterize burst pressure is a more promising approach.

The EC data set consisted of differential bobbinprobe voltage signals taken along the axis of each tube at four test frequencies (400, 200, 100, and 10 kHz). An ac frequency of 10 kHz gives a penetration depth far deeper than the thickness of a steam generator tube wall. Although EC readings taken at this frequency are useful in quickly locating tube support plates and other structures, their use in identifying and characterizing tube defects is minimal. Thus, this analysis was based on the other three frequencies. The amplitudes of the voltage signals for the fourteen tubes were normalized and their phases rotated based on EC measurements of tubes with standard notches.

160

5.2.Neutral Network Study Based on Raw Eddy Current Readings

As a first attempt to analyze the data set, signal features that could be used as neural network input variables were extracted directly from the original eddy current readings. That is, the deconvolution technique was not applied to the data. The candidate signal features included the radial vector lengths and radial vector angles for each of the three ac test frequencies (Fig. 1) along with numerous other Lissajous-pattern characteristics.

For this study feedforward artificial neural networks were trained using software that employs the method of conjugate gradients to improve the learning process.(45) ANN testing was performed with a separate program. Parametric studies were performed to determined which combination of features best predicted tubing burst pressure. In all cases, a leave-one-out (single-dropout) crossvalidation technique was used to assess the ANNs. This assessment technique is appropriate when only small data sets are available for training and testing. For a data set with, say, ten tubes, nine tubes would be used for ANN training; the tenth would be used as an unknown test case. The ANN prediction for the tenth case would be compared with the known burst pressure for that tube. The process would then be repeated such that ten ANN models would be trained, each with a different dropout tube used for testing. In addition to examining various EC signal features, the parametric studies also considered the dependence of the burst pressure predictions on the ANN architecture (i.e., on the number of hidden layers and the number of nodes in each hidden layer). Furthermore, the ANN models were optimized in terms of the fixed convergence criterion selected or, alternatively, in terms of the fixed number of training iterations. The standard deviation of the residuals between the ANNpredicted burst pressures and the measured burst pressures was used to judge the quality of each ANN.

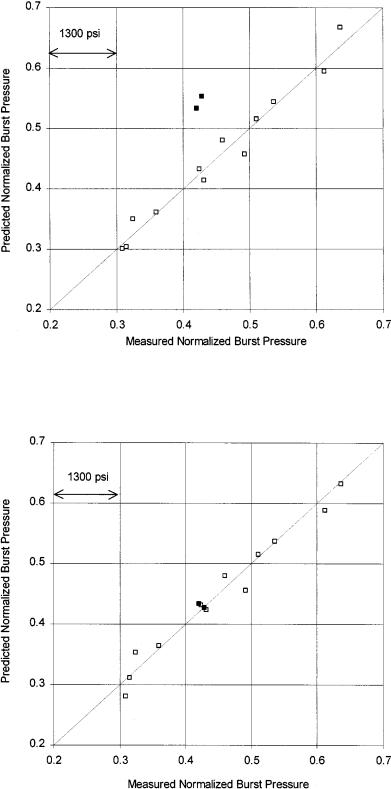
The parametric studies showed that the best ANN models required five EC signal features as input variables, features that could be related to crack length, crack depth, and the volumetric extent of cracking. The studies also showed that two of the fourteen tubes had consistently poor ANN predictions. These outliers were removed from the ANN training set. A plot of predicted burst pressure versus measured burst pressure is presented in Fig. 8. Here, each open symbol represents the ANN prediction of a tube when the model was trained using the remaining eleven tubes. The standard deviation of the ANNpredicted burst pressures about the 458 line is 258 psi, an average error on the order of 4%. The worst burst pressure prediction residual is less than 450 psi. This

Petri et al.

result is a substantial improvement over previous reported attempts to predict tubing burst pressure from EC inspection signals. We recognize, however, that the generalization capability of the ANN model is limited because of the sparse data available.

An important caveat to these ANN modeling results, of course, is that two outliers were not included. The solid symbols in Fig. 8 are the predictions for the outliers tubes using an ANN trained with the remaining twelve tubes. In both cases, the ANN model greatly over-pre- dicted the burst pressure—by up to 1650 psi. It could be that these cases represent a different tubing failure mechanism than the other tubes or that additional variables were not accounted for. As will be shown in the next section, however, the true explanation for the outliers is that the crack-related Lissajous-pattern lobes could not be correctly identified from the original eddy current voltage data. The signal deconvolution technique can be used to make the correct identifications.

5.3.Neural Network Study Based on Deconvolved Eddy Current Readings

To demonstrate the usefulness of the deconvolution technique, the data set was re-analyzed using the eddy current signal deconvolution procedure described in Section 4. Signal features were extracted from the Lissajouspattern crack lobes generated through the deconvolution. ANNs were trained and tested using the same EC signal features as determined through the earlier parametric studies. A new parametric analysis was used to determine the optimal ANN architecture and convergence criterion. The best ANN architecture had a single-dropout standard deviation of 236 psi (Fig. 9), an improvement of 22 psi over the ANNs based on the original (un-deconvolved) data. More significant, the two tubes that were dismissed as outliers in the first analysis were successfully predicted by the new ANNs. That is, signal deconvolution resulted in a more accurate identification of the critical crack in the EC signals, which allowed for a better ANN analysis.

The leave-one-out cross-validation technique, though useful in comparing different ANN models, may not provide accurate estimates of the model errors for each tube prediction. For example, the prediction for a dropout tube may depend heavily on the presence in the training set of a tube with a similar burst pressure and signal features. That is, if not for that particular training tube, the model prediction for the dropout case would be substantially different. Instead, errors for each tube are better estimated through a multiple-dropout cross-valida- tion analysis, which consists of constructing a large number of random training sets from the original data set.

For example, for the tubes in a given data set, one random set may include three replicates of tube 1 and two replicates of tube 2, but may not include tubes 3, 5, and 7. An ANN model is trained for each of these random sets and testing is performed on all dropouts (the tubes not used for training).

In the multiple-dropout cross-validation technique, one can calculate for each tube a mean ANN burst pressure prediction and a standard deviation about that mean over the number of ANN models for which that tube was a dropout. The standard deviations calculated in this manner indicate the sensitivity of the ANN predictions for a given tube to the absence of groups of tubes from the training set. Moreover, the spread of the mean ANN predictions from the measured burst pressures can be quantified as a standard deviation. This value gives a sense of the overall quality of the ANN architecture.

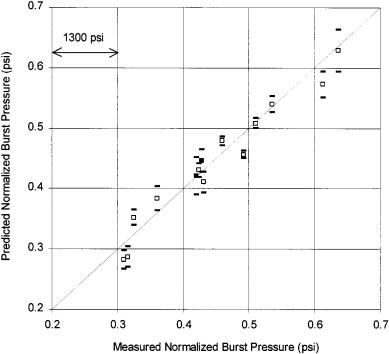
A multiple-dropout analysis was performed for the final ANN architecture. One hundred ANN models were created from training sets of fourteen randomly selected tubes created from the original fourteen tubes. Each model was tested on the remaining tubes not used for training. The results are presented in Fig. 10, which displays the mean predictions and one standard deviation for each dropout tube. The standard deviation of the residuals of the mean predictions was 299 psi. In compari-

son, the multiple-dropout standard deviation for the ANNs using undeconvolved data was 384 psi. This result demonstrates that the final ANN modeling is robust. Predictions were still good even when training was based on very few tubes. Notable in Fig. 10 are the results of the two tubes previously identified as outliers. The burst pressure estimates were consistently accurate even with multiple dropouts in the training set. This improvement in modeling performance was possible once a proper identification of the crack-related Lissajous-pattern lobes could be made through the peak deconvolution technique.

The current ANN results represent a substantial improvement over previous attempts by other researchers to predict tubing burst pressure from EC inspection signals. Nevertheless, some qualifications should be noted:

1.The data set is extremely small, limiting the confidence of the ANN predictions.

2.The tube defects were created in a controlled environment and do not include complexities found in field data.

3.The tube defects simulate axial cracks at tube support plates; other defect geometries have not been considered.

4.Leave-one-out cross-validation testing was used to optimize the ANN architecture. This approach does

Eddy Current Signal Deconvolution

not represent an independent validation of the ANNs and may overestimate the predictive capabilities of the models.(25)

6. CONCLUSIONS

Degradation of steam generator tubing continues to be a critical issue for the nuclear power industry. Eddy current inspection techniques can readily detect abnormalities in the tubes. Eddy current signals are complicated, though, so it has proven difficult to use them in the characterization of flaws and in the assessment of tube integrity. One complication is that voltage signals that arise from the presence of a crack are often obscured by signals from other sources, such as tube support plates. Because of the ambiguities of the EC signals, nuclear utilities must plug or repair a tube upon detection of a flaw, regardless of its likely effect on burst pressure. These costly remedies are often unwarranted.

In this study a new signal processing technique has been described to deconvolve raw eddy current signals into separate Gaussian peaks that represent signal contributions from different sources. From the individual peaks, signals associated with the dominant crack can be identified. Signal features extracted from those specific crackgenerated peaks can then be used for predicting the burst pressure of the tube.

As an example, eddy current and burst pressure data for tubes subjected to an aggressive environment were analyzed with the deconvolution technique and were modeled with artificial neural networks. The ANN predictions were significantly more accurate than results reported in previous investigations. The current study, therefore, demonstrated the potential improvement in modeling that can be achieved through signal deconvolution. Nevertheless, several challenges must be addressed before it can be fully automated for use in the field. In particular, the method still requires expert judgment to determine the best peak fit for the EC voltage signal and to select the combination of fitted peaks that represents the critical tube flaw.

Eddy current signals for tubes pulled from service are often more complex than those from tubes with labora- tory-grown cracks. Pulled tubes can have signals from small cracks and crack networks that are further obscured by the presence of tube support plates, crevice deposits, and other defects. Nonetheless, preliminary attempts to assess pulled-tube data through the combination of signal deconvolution and neural network modeling have been promising.

163

ACKNOWLEDGMENTS

The authors thank Dr. S. Bakhtiari for useful suggestions and discussions. The data used in this study were provided by the U.S. Nuclear Regulatory Commission as part of its ongoing steam generator tube integrity program at Argonne National Laboratory. This work was supported by the U.S. Department of Energy, Science and Technology, under contract W-31-109-ENG-38.

REFERENCES

1.S. J. Green, “Steam Generator Failure or Degradation,” in Metals Handbook, 9th ed., Vol. 13 (Metals Park, Ohio: ASM International, 1987), pp. 937–945.

2.D. R. Diercks, W. J. Shack, and J. Muscara, “Overview of Steam Generator Tube Degradation and Integrity Issues,” in TwentyFourth Water Reactor Safety Information Meeting, Vol. 2, Nuclear Regulatory Commission, NUREG/CP-0157, 1997, pp. 297–312.

3.Interim Plugging Criterion Task Group, “Voltage-Based Interim Plugging Criteria for Steam Generator Tubes,” Nuclear Regulatory Commission, NUREG-1477, June 1993.

4.P. Rodriguez and B. Raj, “Development of In-Service Inspection Techniques for Nuclear Power Plants in India,” Int. J. Pres. Ves. & Piping, 73, 59–68 (1997).

5.F. Cattant, “Lessons Learned from the Examination of Tubes Pulled from Electricite´ de France Steam Generators,” Nucl. Eng. Des., 168, 241–253 (1997).

6.R. Comby, “Secondary Side Corrosion in Steam Generator Tubes: Lessons Learned in France from the In-Service Inspection Results,” Nucl. Eng. Des., 168, 255–259 (1997).

7.G. Frederick, P. Hernalsteen, and D. Dobbeni, “Belgian Approach to Steam Generator Tube Plugging for Primary Water Stress Corrosion Cracking,” Belgatom, EPRI NP-6626-M, March 1990.

8.E. L. Murphy and E. J. Sullivan, “Steam Generator Tube Integrity— U.S. Nuclear Regulatory Commission Perspective,” in TwentyFourth Water Reactor Safety Information Meeting, Vol. 2, Nuclear Regulatory Commission, NUREG/CP-0157, 1997, pp. 313–322.

9.C. J. Denton, “Eddy Current Inspection Systems for Steam Generator Tubing in Nuclear Power Plants,” in Eddy Current Nondestructive Testing, ed. G. M. Free (Washington, D.C.: National Bureau of Standards, 1981), pp. 57–61.

10.L. de la Pintiere, “Multifrequency Eddy Current Examination of Heat Exchanger Tubing,” in Electromagnetic Methods of Nondestructive Testing, ed. W. Lord (New York: Gordon and Breach Science Publishers, 1985), pp. 195–305.

11.D. E. Bray and R. K. Stanley, Nondestructive Evaluation: A Tool in Design, Manufacturing, and Service (New York: CRC Press, Inc., 1997).

12.“Eddy Current Examination of Tubular Products,” ASME Boiler and Pressure Vessel Code: An International Code, Section V, Article 8 (New York: The American Society of Mechanical Engineers, 1998), pp. 161–177.

13.T. Stepinski, “Analysis of Eddy Current Patterns,” British J. NDT, 32, 631–633 (1990).

14.B. Benoist, P. Gaillard, M. Pigeon, and P. Morizet-Mahoudeaux, “Expert System for the Characterization of Defect Signals in Steam Generator Tubes,” Eng. Appl. Artif. Intell., 8, 309–318 (1995).

15.B. R. Upadhyaya, W. C. Hooper, M. M. Behravesh, and G. Henry, “Automated Diagnosis of Steam Generator Tubing by Eddy-Current Testing,” Trans. Am. Nucl. Soc., 78, 181 (1998).

16.C. F. Morabito, “Independent Component Analysis and Feature Extraction Techniques for NDT Data,” Mater. Eval., 58(1), 85–92 (Jan. 2000).

164

17.B. Georgel and R. Zorgati, “EXTRACSION: A System for Automatic Eddy Current Diagnosis of Steam Generator Tubes in Nuclear Power Plants,” in Non-Destructive Testing 92, Vol. 1, eds. C. Hallai and P. Kulcsar (New York: Elsevier Science Publishers B.V., 1992), pp. 278–282.

18.A. J. Levy, et al., “Dodger: An Expert System for Eddy Current Evaluation,” Mater. Eval., 51 (1), 34–44 (Jan. 1993).

19.“Eddy Current Sizing Technique Found Invalid,” Nuclear News, 40(7), 20 (June 1997).

20.P. G. Doctor, et al., “Pattern-Recognition Methods for Classifying and Sizing Flaws Using Eddy-Current Data,” in Eddy-Current Characterization of Materials and Structures, eds. G. Birnbaum and G. Free (Philadelphia, Penn.: American Society for Testing and Materials, 1981), pp. 464–483.

21.R. J. Kurtz, et al., “Steam Generator Tube Integrity Program / Steam Generator Group Project: Final Project Summary Report,”

Pacific Northwest Laboratory, NUREG/CR-5117, May 1990.

22.J. Jarmulak, P. P. van’t Veen, and E. J. H. Kerckhoffs, “Use of Case-Based Reasoning for Interpretation of Data from NDT,” INSIGHT, 41, 642–649 (1999).

23.J. H. Garrett, Jr., D. J. Gunaratnam, and N. Ivezic, “Introduction,” in Artificial Neural Networks for Civil Engineers: Fundamentals and Applications, eds. N. Kartam, I. Flood, and J. H. Garrett, Jr. (New York: American Society of Civil Engineers, 1997), pp. 1–18.

24.L. Tarassenko, A Guide to Neural Computing Applications (New York: John Wiley & Sons Inc., 1998).

25.J. A. Burns and G. M. Whitesides, “Feed-Forward Neural Networks in Chemistry: Mathematical Systems for Classification and Pattern Recognition,” Chem. Rev., 93, 2583–2601 (1993).

26.R. Sikora, et al., “Identification of Flaws Using Eddy Current Testing,” COMPEL Int. J. Comput. Math. Electr. Electron. Eng.,

17, 516–527 (1998).

27.T. Chady, M. Enokizono, and R. Sikora, “Crack Detection and Recognition Using an Eddy Current Differential Probe,” IEEE Trans. Magn., 35, 1849–1852 (1999).

28.L. Udpa and S. S. Udpa, “Eddy Current Defect Characterization Using Neural Networks,” Mater. Eval., 48, 342–347 (1990).

29.H. Komatsu, et al., “Basic Study on ECT Data Evaluation Method with Neural Network,” in Non-Destructive Testing 92, Vol. 1, eds. C. Hallai and P. Kulcsar (New York: Elsevier Science Publishers B. V., 1992), pp. 322–326.

30.C. V. Dodd, J. R. Pate, and J. D. Allen, Jr., “Improved EddyCurrent Inspection for Steam Generator Tubing,” Oak Ridge National Laboratory, CONF-8910222-7, 1989.

Petri et al.

31.C. V. Dodd and J. R. Pate, “Improved Eddy-Current Inspection for Steam Generator Tubing,” Oak Ridge National Laboratory, CONF- 9010185-9, 1990.

32.C. V. Dodd and J. R. Pate, “Advancement in Eddy-Current Technology for Steam Generator Tube Inspection,” in Twentieth Water Reactor Safety Information Meeting, Vol. 3, Nuclear Regulatory Commission, NUREG/CP-0126, 1990, pp. 267–276.

33.C. V. Dodd, “Data Analysis for Steam Generator Tubing Samples,” Oak Ridge National Laboratory, NUREG/CR-6455, ORNL/ TM-13206, 1996.

34.B. R. Upadhyaya and W. Yan, “Hybrid Digital Signal Processing and Neural Networks for Automated Diagnostics Using NDE Methods,” The University of Tennessee, NUREG/GR-0010, Nov. 1993.

35.W. Yan and B. R. Upadhyaya, “An Integrated Signal Processing and Neural Networks System for Steam Generator Tubing Diagnostics Using Eddy Current Inspection,” Ann. Nucl. Energy, 23, 813– 825 (1996).

36.S. J. Kang and Y. R. Kwon, “Hybrid Knowledge-Based Architecture for Building an Intelligent Nondestructive Signal Inspection System,” Knowledge-Based Systems, 8(1), 21–31 (Feb. 1995).

37.B. R. Upadhyaya, W. Yan, M. M. Behravesh, and G. Henry, “Development of a Diagnostic Expert System for Eddy Current Data Analysis Using Applied Artificial Intelligence Methods,” Nucl. Eng. Des., 193, 1–11 (1999).

38.S-J Song and Y-K Shin, “Eddy Current Flaw Characterization in Tubes by Neural Networks and Finite Element Modeling,” NDT E. Int., 33, 233–243 (2000).

39.L. A. Wainstein and V. D. Zubakov, Extraction of Signals from Noise, (Englewood Cliffs, N. J.: Prentice-Hall, Inc., 1962).

40.C. V. Dodd, J. R. Pate and J. D. Allen, “Advancement in EddyCurrent Test Technology for Steam Generator Tube Inspection,” Mater. Eval., 53(1), 49–54 (Jan. 1995).

41.L. D. Sabbagh and H. A. Sabbagh, “Eddy-Current Modeling and Flaw Reconstruction,” J. Nondestructive Evaluation, pp. 95–110, Vol. 7, Nos. 1/2, 1988.

42.B. A. Auld, “Probe-Flaw-Interactions with Eddy-Current Array Probes,” in Review of Progress in Quantitative Nondestructive Evaluation, Vol. 10A, eds. D. O. Thompson and D. E. Chimenti (New York: Plenum Press, 1990), pp. 951–956.

43.PeakFit, Version 4.05, SPSS Inc., Chicago, Illinois (1997).

44.D. Stellfox, “Argonne Steam Generator Mock-Up Could Improve Inspection Effort,” Nucleonics Week, 41(17), 7–8 (April 27, 2000).

45.J. Reifman and J. E. Vitela, “Accelerating Learning of Neural Networks with Conjugate Gradients for Nuclear Power Plant Applications,” Nucl. Technol., 106, 225–241 (1994).