
Lek_26-33_Cher
.pdf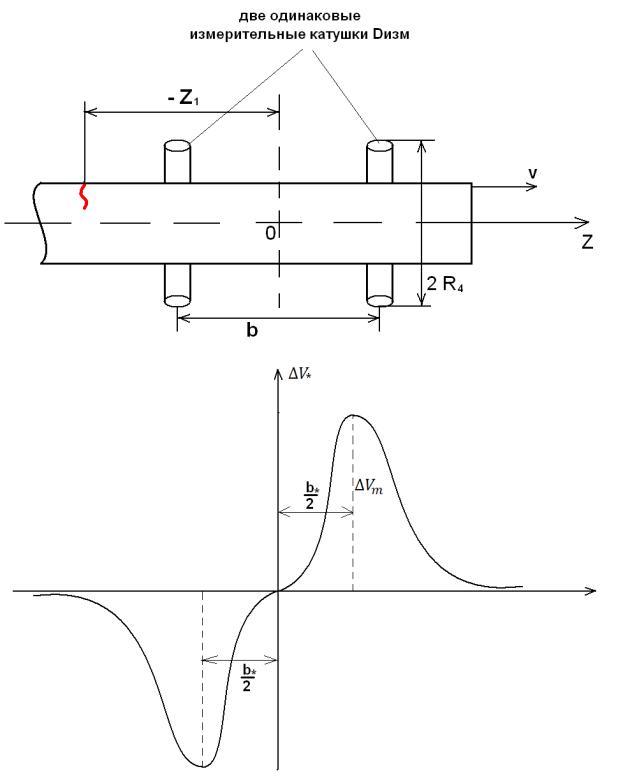
Сигналы дифференциального проходного ВТП от точечных дефектов
Рисунок 14
Можно аппроксимировать кривую выражением:
|
|
|
4t 2 |
2b2 |
|
|
2 |
b |
|
||
u* (t) 2um* |
|
|
|
|
0 * |
|
sh |
|
0 |
* |
t |
|
|
|
|
|
|
||||||
( ) exp |
2 |
2 |
|
|
|
2 |
|
||||
|
|
|
И |
|
|
|
И |
|
|
||
И длительность импульса определяется по уровню 0,6.
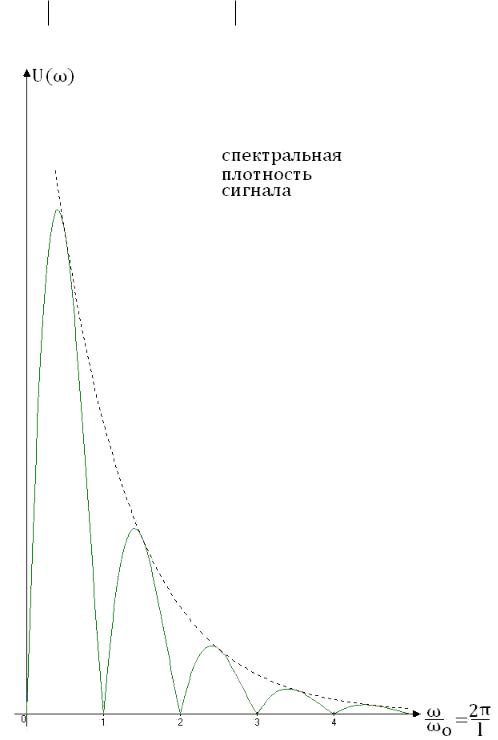
Нас интересует спектральный анализ.
Для спектра сигнала:
v( ) 2 vm ( )sin(0,5b* 0 ) exp( 0,0186 2 02 )
Можем построить график:
Рисунок 15
(1)
(2)
Вывод:
спектр не имеет постоянной составляющей;
зависит от базы (от базы зависит положение нулей).
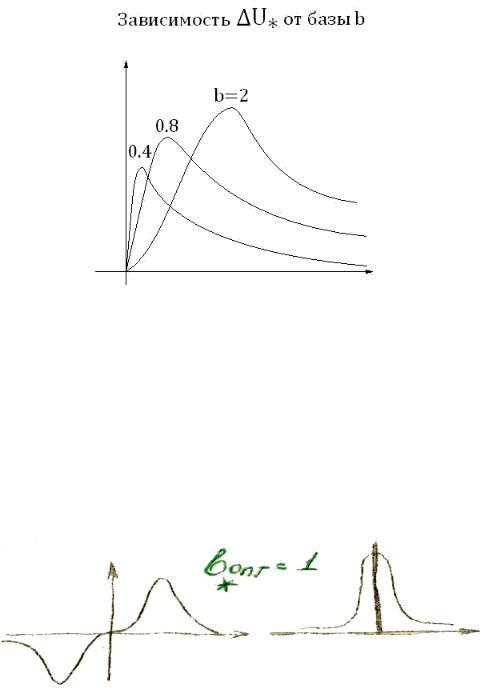
Зависимость амплитуды и формы импульсов сигналов ВТП от базы b
Изображаем графически в виде семейства кривых:
Рисунок 16
Вывод:
-форма импульса не зависит от базы;
-наибольшее значение импульса уменьшается с уменьшением базы.
При b* 1 наибольшее значение импульса отличается от наибольшего значения импульса абсолютного преобразователя не более, чем на 20%.
При b* 1 получаем оптимальные условия контроля.
Рисунок 17
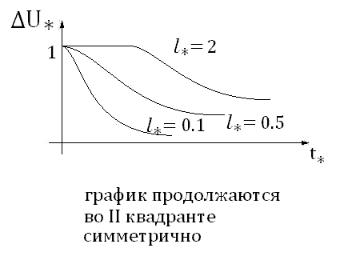
Для подавления влияния мешающих факторов выгодно базу уменьшать.
Влияние длины и формы дефектов на форму импульсов сигналов ВТП
На практике чаще встречаются не точечные, а протяженные вдоль оси дефекты.
Влияние длины дефектов на амплитуду сигналов рассмотрели в статическом режиме.
Здесь анализируем только форму. Нормируем каждый импульс по своему max значению.
1. для абсолютного ВТП:
Рисунок 18
l* |
|
e |
|
|
|
|
|||
2RИ |
нормировка по диаметру измерительной катушки |
|||
|
|
|||
|
|
|
Вывод:
- наибольшее значение импульса достигается при z и t* 0 для абсолютного ВТП;
- при l* 0,5 |
И * |
l* |
длительность импульса примерно равна длине дефекта; |
- при l* 0,5 |
И * |
l* |
и при l* 0,2 практически зависимости от l* нет, можно считать |
дефект точечным. |
|
|
|
2. для дифференциального ВТП:
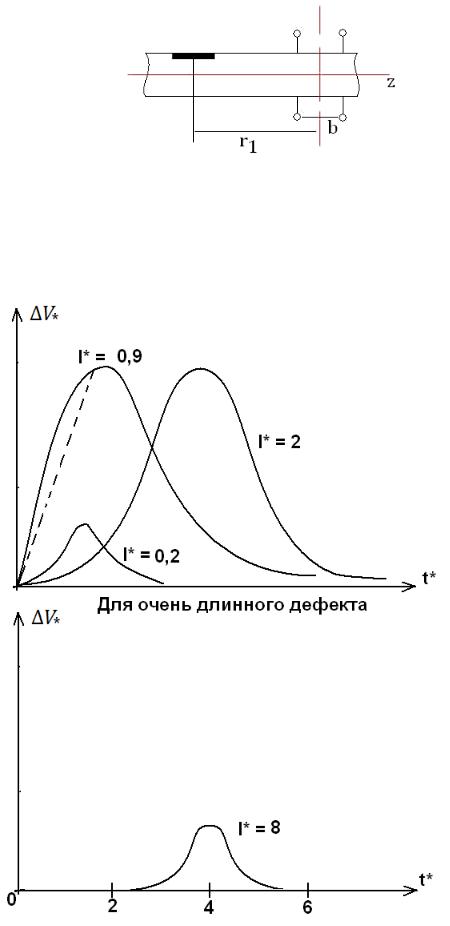
Рисунок 19
Определяем расстояние до середины длины дефекта.
Рисунок 20
Вывод:
-для длинного дефекта дифференциальный преобразователь фиксирует только его начало и конец;
-при l* 2 форма импульса мало зависит от l* , а между наибольшими значениями импульсов расстояние равно длине дефекта.
Форма сигналов накладных ВТП от точечных дефектов
Вопрос изучен существенно меньше, задача трехмерная.
Рисунок 21
Введем относительные координаты :
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
t |
|
|
|
|
|
|
|
|
v |
|
|
|
t |
|
|
||||||
* |
|
|
|
|
|
* |
|
||||||||||
|
|
|
|
RЭ |
|
|
|
RЭ |
|
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
||
|
|
|
RЭ |
|
- время прохождения дефекта через R |
|
|||||||||||
0 |
|
|
Э |
||||||||||||||
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
RЭ радиус эквивалентного контура вихревых токов в объекте
В первом приближении принимаем RЭ R ( RЭ RЭ (R, h) )
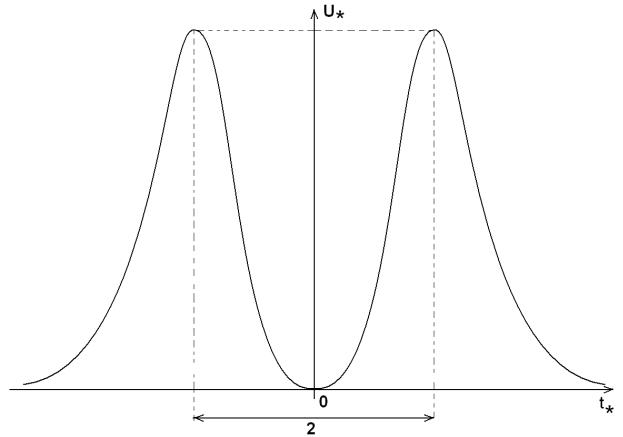
Огибающая сигналов:
Случай прохождения дефекта через центр катушки
Рисунок 22
Max соответствие нахождению дефекта под витком.
Аппроксимируем кривой:
u(1) v |
t 2 |
exp( |
t |
)2 |
|
|
|
|
|||
2 |
|
0 |
(3) |
||
0 |
|
|
|||
Под v понимается напряжение на выходе ВТП в отсутствие дефекта.
В зависимости от траектории движения дефекта вдоль оси преобразователя форма импульса будет меняться.
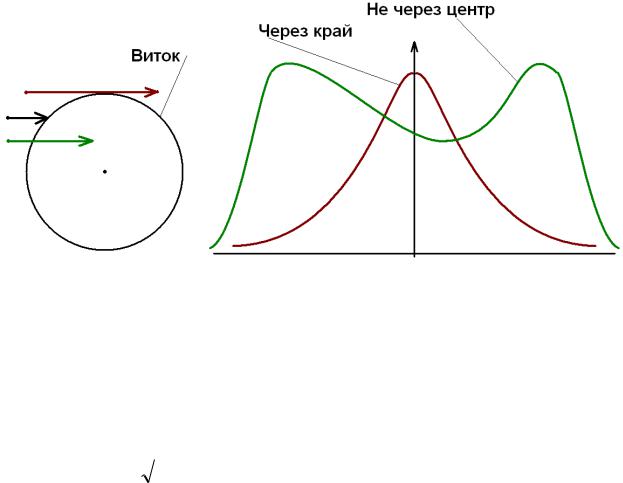
Рисунок 23
Max уменьшается и ноль достигаться не будет.
Если проходит через край, то вообще один max.
Выражение для спектра:
|
|
|
(1 0,125 2 02 ) exp( 0,25 2 2 ) |
v( ) 0,5 |
v 0 |
||
|
|
|
(4) |
Определение параметров дефектов при модуляционной вихретоковой дефектоскопии
Переход от дефектоскопии к дефектометрии становится актуальной задачей на современном этапе развития неразрушающего контроля.
Исследование возможности определения параметров дефектов при модуляционном способе электромагнитной дефектоскопии с помощью проходных преобразователей сводится к определению сигналов преобразователей от произвольно расположенных дефектов конечных размеров. Ввиду значительных математических трудностей в строгой постановке такая задача пока не разрешена.
Имеется приближенное решение этой задачи для накладного преобразователя. И экспериментально полученные зависимости сигнала от дефекта. Сигналы проходного преобразователя по приближенной методике Берроуза. Основное внимание уделяется выбору оптимального значения обобщенного параметра :  , где R —радиус изделия; σ —
, где R —радиус изделия; σ —
удельная электрическая проводимость материала изделия; μ0 — магнитная постоянная) для различных случаев взаимного расположения преобразователя и изделия с дефектом.
Анализируется также форма импульса сигнала, соответствующая прохождению точечного дефекта через дифференциальный проходной преобразователь.

Для модуляционного способа дефектоскопии необходимо знать форму огибающей высокочастотного сигнала от дефекта при движении изделия с поверхностным дефектом конечной длины относительно преобразователя. Знание формы или частотного спектра этого сигнала позволит применить оптимальные фильтры для выделения сигналов на фоне помех. Имеется приближенный метод расчета формы огибающей сигнала проходного дифференциального трансформаторного преобразователя с однородным монохроматическим возбуждающим магнитным полем при движении изделия с дефектом. При следующих допущения:
распределение плотности вихревых токов в объекте контроля с продольным поверхностным дефектом конечной длины такое же, как в случае бесконечно длинного дефекта такого же поперечного сечения;
искажение распределения плотности вихревых токов на краях дефекта и влияние скорости движения объекта контроля на распределение вихревых токов не учитываются.
Очевидно, что при уменьшении длины дефекта погрешность расчетов будет возрастать в силу сделанных допущений. Однако, как показано ниже, при определении формы сигнала преобразователя от короткого дефекта это несущественно, поскольку форма сигнала в этом случае определяется в основном параметрами преобразователя, а не длиной дефекта.
Напряжение вносимое в измерительную катушку преобразователя под влиянием дефекта, можно представить в виде
вносимое в измерительную катушку преобразователя под влиянием дефекта, можно представить в виде
где М — взаимная индуктивность элементарного объема изделия и измерительной обмотки преобразователя; .δ — плотность вихревых токов в элементарном объеме изделия без дефекта; δД — то же для изделия с дефектом бесконечной длины; dV — элемент объема объекта контроля. Интегрирование ведется по объему V участка изделия с дефектом, так как в остальных случаях плотность вихревых токов дефектного изделия «е отличается от плотности вихревых токов в элементарном объеме бездефектного изделия. Однако и в этом случае расчет напряжения измерительной катушки преобразователя остается довольно сложным, так как аналитические выражения распределения плотности вихревого тока в сечении изделия с дефектом имеются лишь для ограниченного диапазона изменения обобщенного параметра х. Такие задачи решаются методом математического моделирования.
Для больших значений параметра х настил тока численно равен напряженности магнитного поля на поверхности изделия
Расчеты упрощаются при больших значениях обобщенного параметра х, когда вихревые токи сосредоточены в тонких поверхностных слоях и почти вплотную огибают дефект. В этом случае изделие с дефектом можно заменить эквивалентной катушкой (или металлической полосой) с током, причем форма витков катушки повторяет форму поверхности изделия. Вносимое в измерительную катушку напряжение можно определить, рассчитав величину взаимной индуктивности между измерительной и эквивалентной катушками. Ток на единицу длины изделия можно представить, как настил тока.
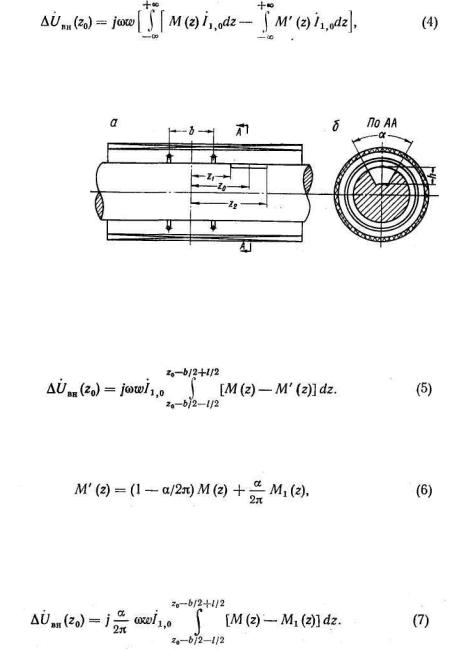
На рис. 1 изображен круговой цилиндр с продольным дефектом, расположенный в однородном продольном магнитном поле проходного преобразователя. Встречно включенные измерительные катушки с числом витков w в каждой расположены симметрично относительно середины возбуждающей. Расстояние между катушками (база) равно Ь. Ось z совпадает с осью изделия и катушек, начало оси z совмещено с серединой возбуждающей катушки. Середина поверхностного дефекта длиной l=z2—z1) находится на расстоянии Z0 от середины возбуждающей катушки. Поперечное сечение объекта контроля в виде длинного кругового цилиндра с дефектом показано на рис. 1б. Боковые стороны дефекта глубиной h совпадают с радиусами цилиндра, угол между которыми равен α. Основание дефекта совпадает с дугой окружности радиуса (R-h).
Приращение напряжения  (z0) вносимое дефектом в правую измерительную катушку преобразователя (рис. 1а), может быть подсчитано по формуле
(z0) вносимое дефектом в правую измерительную катушку преобразователя (рис. 1а), может быть подсчитано по формуле
где M(z) —взаимная индуктивность витка измерительной катушки и элементарного контура шириной dz бездефектного (образцового) цилиндра; Mr(z) —то же для цилиндра с дефектом.
Рисунок 24. Объект контроля в проходном преобразователе
Учитывая, что взаимная индуктивность М' (z) равна M(z) на всей длине цилиндра за исключением участка (z2— z1), и полагая настил тока в дефектном участке равным настилу тока в образцовом цилиндре
Взаимная индуктивность для элемента dz на дефектном участке может быть представлена,
как
выражение (4) можно преобразовать к виду, где М1 (z) — взаимная индуктивность витка измерительной катушки и кругового контура диаметром (2R – 2h). Подставив выражение (6) в (5), получим
При дифференциальном включении измерительных катушек преобразователя (см. рис. 1) приращение сигнала, вызванное дефектом, определяется выражением
