В каждой лекции все формулы, определения и теоремы нумеруются так же, как и в предыдущей лекции, с цифры 1 (т.е. нумерация не продолжается от лекции к лекции). Это удобно при чтении лекций.

Лекция 1. Пространство геометрических векторов. Линейные операции над векторами. Скалярное, векторное и смешанное произведение векторов, их вычисление в координатной форме и геометрический смысл

1. Векторы. Координаты векторов и линейные операции над векторами

Множество всех геометрических векторов в трехмерном пространстве обозначают буквой 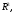а множество всех векторов на плоскости – буквой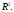Ниже все понятия и утверждения формулируютя для пространства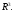Ясно, что они очевидном образом переносятся и на пространство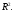Перейдем к изложению основных понятий.

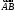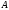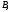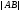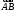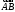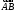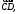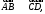Определение 1. Вектором называется направленный отрезок с начальной точкойи конечной точкойпричем два вектора считаются р̀авными, если один из них получен из другого параллельным переносом(см. Р1). Длинанаправленного отрезканазывается длиной вектора. Векторыилежащие на одной прямой или на параллельных прямых называются коллинеарными; если при этом их направления совпадают, то пишута если они имеют противоположные направления, то пишут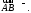Таким образом,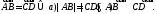Если начало и конец вектора совпадают, то такой вектор называется нулевым (обозначение: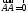). Считают, что нулевой вектор коллинеарен любому другому вектору и имеет произвольное направление.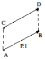

Заметим, что векторы обозначаются также малыми латинскими буквами:

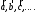
Напомним, что осью (в пространстве или на плоскости) называется прямая с выбранной на ней (положительным) направлением и масштабом (единицей измерения). Обозначение: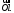При этом каждой точке оси соответствует единственное действительное число, и обратно: каждому действительному числу числу соответствует единственная точка на числовой оси. Единичный вектор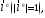лежащий на оси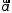и направленный так же, как ось, называетсяортом оси

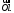
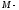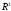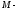Пусть произвольная точка в пространстве( или на плоскости). Проведем черезплоскость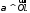Тогда точка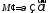называетсяпроекцией точки 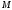на ось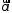(обозначение: ).

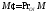Определение 2. Если 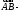вектор, то вектор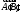где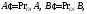называетсягеометрической проекцией вектора 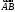на ось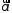(см.Р2) а число

называется просто проекцией вектора 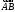на ось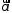и обозначается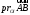(обратите внимание на различие в написаниях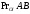и ).

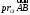В пространстве 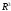рассмотрим декартовую систему координат, определяемую осями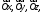с ортами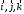соответственно.

Определение 3. Числа 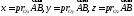называются координатами вектора 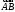в декартовой системе координат. Обозначение:

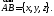
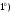Если 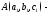начало вектор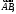аа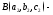конец вектора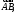то=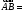

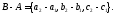
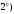Орты осей декартовой системы координат 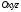имеют следующие координаты: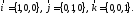

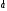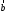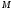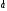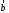Определим теперь линейные операции над геометрическими векторами. Выпустим векторы ииз общего началаи построим параллелограмм со сторонамии. Пусть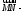диагональ этого параллелограмма.

1. Суммой двух векторов 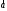и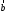называется вектор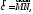совпадающий с диагональю параллелограмма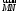, построенного указанным образом на векторах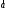и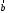(см.Р3).

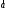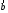2. Разностью векторов и называется такой вектор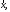что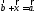Обозначение:

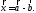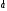Если векторы и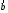имеют общее начало, то вектор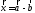будет совпадать с вектором, выпущенным из конца вектора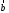в конец вектора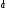(см.Р4).

3. Произведением вектора 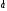на число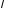называется вектор 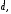имеющий длину 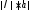и направленный так же, как 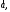иесли 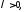и противоположно векторуесли

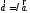Обозначение: Если же 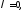то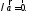

Введенные операции над векторами (их называют линейными операциями) обладают свойствами аналогичных операций для чисел (свойства асоциативности, коммутативности, дистрибутивности и т.д.), которые используются при вычислениях. Например,

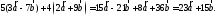
Из определения коллинеарных векторов вытекает, что

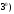векторы 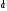и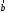коллинеарны тогда и толко тогда, когда существует число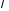такое, что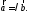

Теперь ясно, что по векторам и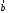можно построить любую их линейную комбинацию

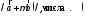Используя геометрические соображения, легко доказать следующее утверждение.

Теорема 1. Любой вектор 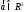может быть разложен в линейную комбинацию ортов 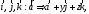причем это разложение единственно, а числаявляются

координатами вектора 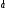в выбранной декартовой системе координат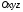

Замечание 1. Ниже будет дано определение базиса в 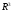и будет показано что орты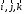образуют базис в 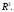Кроме того, будет показано, что в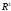существует бесконечное множество базисов. Базис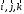обычноназываютстандартным базисом в .

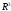Теорема 1 устанавливает взаимно однозначное соответствие между векторами пространства 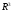и упорядочными тройками чисел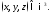Именно: каждому вектору

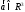соответствует единственная упорядочная тройка чисел 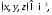гдекоординаты векторав базисеи наоборот: каждой упорядочной тройке чисел 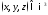соответствует единственный вектор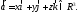Поэтому часто оттождествляют векторы и их координаты и пишут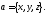При этом вместо того, чтобы совершать геометрически линейные операции над векторами совершают их аналитически, в координатной форме. Это оправдывается следующим утверждением.

Теорема 2. Пусть векторы 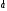и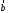заданы своими координатами: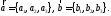Тогда их линейная комбинация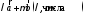в координатной форме имеет вид

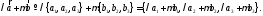
Доказательство. Имеем

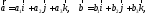
поэтому

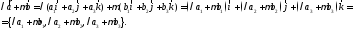
Теорема доказана.

Используя теорему о диагонали прямоугольного параллелепипеда, легко доказать следующее утверждение.

Теорема 3. Если вектор 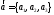задан своими координатами в базисе 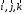, то его длина вычисляется по формуле

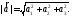
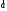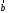Определение 4. Углом между векторами иназывается угол, на который нужно повернуть первый вектор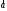до совпадения со вторым вектором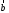против часовой стрелки. Обозначение:

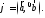
Проекция вектора 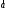на вектор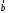определяется так же, как и проекция вектора на ось.

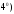Проекция вектора 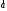на вектор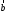вычисляется по формуле

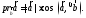
Числа 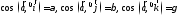называются направляющими косинусами вектора 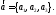Так как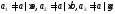и

то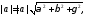поэтому имеет место следующее соотношение между направляющими косинусами вектора : 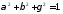Значит, вектор

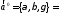
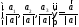₌ является ортом вектора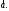

Из 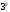вытекает следующее утверждение.

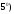Вектор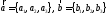ы коллинеарны тогда и только тогда, когда их координаты пропорциональны: