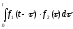- •Курс лекций по предмету
- •История развития тау как науки.
- •Классификация сау. Автоматические системы
- •Пример системы стабилизации на примере стабилизатора напряжения
- •4. Структурная схема сау.
- •5. Принципы управления.
- •Глава 1. Составление и линеаризация дифференциальных уравнений систем автоматизированного управления. Прохождение регулярных сигналов через линейные звенья.
- •1.1 Составление и линеаризация дифференциальных уравнений сау.
- •1.2. Общая характеристика регулярных сигналов.
- •Глава 2. Основные характеристики линейных сау и их звеньев.
- •2.1 Некоторые сведения о прямом и обратном преобразовании Лапласа.
- •Обратное преобразование Лапласа
- •2.2 Передаточная функция и переходная характеристика звена (системы).
- •2.3 Комплексный коэффициент усиления.
- •2.4 Типовые звенья сау.
- •5. Дифференцирующие звенья.
- •6. Упругое (интегро-дифференцирующее) звено.
- •Общие свойства минимально-фазовых звеньев и систем.
- •Виды соединения звеньев в сау.
- •Структурные преобразования схем.
- •Построение асимптотических характеристик линейных непрерывных сау.
- •Порядок построения асимптотических лачх по передаточной функции.
- •Составление дифференциальных уравнений и передаточной функции сау по структурной схеме.
- •Глава 3. Устойчивость линейных непрерывных сау.
- •3.1.Суждение об устойчивости нелинейной системы по её линейному приближению.
- •3.2.Суждения об устойчивости линейной сау.
- •3.3.Критерии устойчивости.
- •Cпособы построения годографа Михайлова
- •Структурно-неустойчивые сау.
- •Глава 4. Стабилизация сау.
- •Определение предельного коэффициента усиления.
- •4.2 Методы стабилизации.
- •Сравнение методов стабилизации.
- •Глава 5. Анализ качества процесса управления.
- •5.1.Приближённые оценки качества переходного процесса.
- •3. Косвенные показатели качества сау.
- •5.2.Точные оценки качества переходного процесса.
- •5.3. Качественные показатели в установившемся режиме.
- •Глава 6. Элементы синтеза сау.
- •6.1 Введение, или общая постановка задач.
- •6.2. Частная постановка задач.
- •Синтез последовательного корректирующего устройства.
- •Синтез последовательного корректирующего устройства в цепи с ос.
1.2. Общая характеристика регулярных сигналов.
Любое САУ может
рассматриваться как некое звено,
преобразовывающее вход ( )
в выход (
)
в выход ( ).
).


Все звенья, рассматриваемые в ТАУ, являются звеньями направленного действия.
Регулярные сигналы:

Дифференциальные
уравнения, связывающие
 и
и ,
полностью определяются характеристиками
звена или системы.
,
полностью определяются характеристиками
звена или системы.
В ТАУ рассматриваются 2 задачи:
Задача анализа:
Дано:
 и дифференциальное уравнение звена или
системы. Найти
и дифференциальное уравнение звена или
системы. Найти при заданных начальных условиях. Эта
задача однозначна.
при заданных начальных условиях. Эта
задача однозначна.
Задача синтеза:
Заданы
 и
и
 .
Найти структуру и характеристики САУ,
которые бы удовлетворяли заданному
значению
.
Найти структуру и характеристики САУ,
которые бы удовлетворяли заданному
значению .
.
Регулярный сигнал на входе может быть любой, но рассмотрим 3 вида сигнала:
Гармонический:
 или
или
Единичный скачок:

 ;
;
Реакция системы на единичнвй скачок, называется переходной характеристикой.

Единичный импульс:

 –весовая
функция.
–весовая
функция.
Оказывается, что:
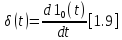
Преобразования Фурье и Лапласа от этих сигналов см. [Нетушил, стр. 385 – 392].
Любой сигнал можно представить в виде совокупности:
-гармонических сигналов;
-единичных скачков;
-единичных импульсов.
Пусть
 – некоторая функция времени. Тогда
выражаем её в виде совокупности
гармонических сигналов, применяем ряд
Фурье для периодических сигналов и
преобразования Фурье для непериодических
сигналов. Применяя интеграл Дюамеля,
функцию
– некоторая функция времени. Тогда
выражаем её в виде совокупности
гармонических сигналов, применяем ряд
Фурье для периодических сигналов и
преобразования Фурье для непериодических
сигналов. Применяя интеграл Дюамеля,
функцию
 можно представить в виде совокупности
единичных скачков.
можно представить в виде совокупности
единичных скачков.


Если рассмотрим линейные звенья, то:



Отсюда:




В виде гармонического сигнала:



Глава 2. Основные характеристики линейных сау и их звеньев.
2.1 Некоторые сведения о прямом и обратном преобразовании Лапласа.
Прямым преобразованием Лапласа называется преобразование, при котором функция действительных переменных преобразуется в функцию комплексных. Дифференциальные уравнения преобразуются в алгебраические.

 -
оригинал;
-
оригинал;
 - изображение
- изображение


Таблица соответствий
|
|
|
|
|
(1) |
|
|
|
(2) |
|
|
|
(3) |
|
|
|
(4) |
|
|
|
(5) |
|
|
|
(6) |
|
|
|
(7) |
|
|
|
(8) |
|
|
|
(9) |
|
|
|
(10) |
|
|
|
(11) |
|
|
|
(12) |
|
1 |
|
(13) |
|
|
|
(14) |
|
|
|
(15) |
|
|
|
(16) |
|
|
|
(17) |
|
|
|
(18) |
|
|
Обратное преобразование Лапласа
Функция комплексных переменных превращается в функцию вещественных переменных.
 (2.1)
(2.1)
Если функция
 не имеет
нулей и полюсов в правой части, то
не имеет
нулей и полюсов в правой части, то
 (2.2)
(2.2)
 - часто
дробно-рациональная функция.
- часто
дробно-рациональная функция.

По физическим
соображениям

Тогда
 (2.3)
(2.3)

Рассмотрим случай, когда

Как видно, один корень нулевой.
Тогда
 (2.4)
(2.4)
2.2 Передаточная функция и переходная характеристика звена (системы).

Передаточная функция называется отношением лапласовского преобразования.
 (2.5)
(2.5)
 (2.5’)
(2.5’)
Переходной
характеристикой называется
закон изменеия во времени или переходной
процесс выходной величины
 при подаче на вход единичного скачка.
при подаче на вход единичного скачка.

 в данном случае
в данном случае
 (2.6)
(2.6)
Импульсная
переходная характеристика (весов.
функция) – переходной
процесс на выходе при подаче на вход
 -импульса.
-импульса.

 (2.7)
(2.7)
Тогда
 (2.7’)
(2.7’)