2.3 Электропроводность полупроводников

2.3.1 Электронная проводимость

При комнатной температуре электроны зоны проводимости хаотически двигаются по кристаллу с тепловой скоростью v_т, его средняя скорость в заданном направлении равна нулю. При этом можно считать, что электроны находятся в тепловом равновесии с нагретой кристаллической решеткой и средняя температура электронов (как мера их кинетической энергии) соответствует температуре кристалла. Средняя тепловая скорость движения электронов будет определяться классическим соотношением:

(2.21)

где v_т ~10⁷ см/с – средняя тепловая скорость электронов, k – постоянная Больцмана.

Электроны взаимодействуют с дефектами кристаллической решетки, между собой и ядрами, изменяя (рассеивая) свою кинетическую энергию. Усредненное значение участков пути, пройденное электроном между актами рассеяния, называются средней длиной свободного пробега. Время между двумя актами взаимодействия – временем свободного пробега: .

При приложении к полупроводнику электрического поля с напряженностью Ē электрон приобретает ускорение , где – эффективная масса электронов у дна зоны проводимости и, соответственно, дополнительную дрейфовую скорость, направленную против поля: , так что, продолжая участвовать в тепловом движении, он постепенно смещается под действием поля.

Рис. 3.2

Электрон под действием электрического поля в твердом теле не может набирать энергию до бесконечности, он провзаимодействует с другим объектом, отдаст ему накопленную энергию (не обязательно всю). Вероятность взаимодействия частиц тем выше, чем меньше их время свободного пробега – τ (зависящая от длины свободного пробега):

(2.22)

_{Коэффициент пропорциональности между дрейфовой скоростью и напряженностью электрического поля называют подвижностью носителей заряда и обозначают μ [см}²_/(В∙с)].

(2.23)

_{Предположим, что ток через образец создается электронами, концентрация которых n см}^-3 _{и средняя дрейфовая скорость vдр. Поскольку величина тока равна заряду, проходящему через сечение образца в единицу времени, плотность тока при слабом электрическом поле По закону Ома}

_. , , , где σ -_{проводимость.}

_{Отсюда легко получить закон Ома в дифференциальной форме:}

Jn = σn·E,

(2.24)

где σ_n – электронная проводимость (Ом∙см).

(2.25)

Проводимость материала определяется двумя основными параметрами: подвижностью носителей заряда и их концентрацией.

Существует несколько механизмов рассеяния энергии свободных носителей заряда. Для полупроводников наиболее важные два: рассеяние в результате взаимодействия с колебаниями решетки (решеточное рассеяние) и рассеяние в результате взаимодействия с ионизованной примесью.

Экспериментальные исследования температурной зависимости подвижности показывают, что при низких температурах преобладает рассеяние на ионах примеси, а при более высоких – рассеяние на тепловых колебаниях решетки.

При рассеянии на заряженной примеси

,

(2.27)

μ_ni~τ~T^3/2. Если в образце доминирует рассеяние на примесях, то с ростом температуры подвижность возрастает.

Для рассеяния на решетке справедливо выражение:

,

(2.26)

то есть с ростом температуры подвижность падает. Действительно, длина свободного пробега носителей заряда тем меньше, чем выше температура решетки (чем сильнее колеблется решетка): l~1/T. Для скорости носителей справедливо v ~ T ^1/2 (mv²=3kT), тогда: μ_r ~ τ = l/v ~ 1/T^-3/2.

При одновременном действии нескольких механизмов рассеяния для расчета подвижности можно воспользоваться понятием эффективной подвижности носителей:

.

(2.28)

Поскольку в собственном полупроводнике отсутствуют примеси, рассеяние электронов и дырок в нем должно происходить только на тепловых колебаниях решетки, т.е. в собственных кристаллах значение подвижности носителей заряда должно быть максимальным.

Рис. Температурная зависимость подвижности носителей заряда с разным уровнем легирования (N1<N2<N3)
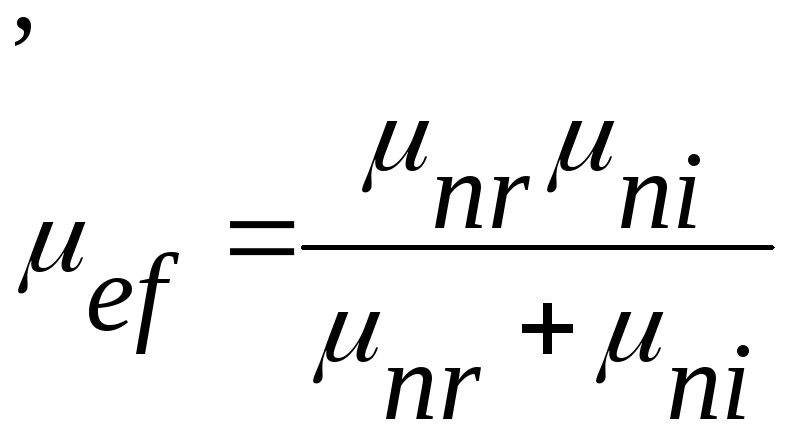