ВМ1(3 семестр)шпоры2

БИЛЕТ 30. Условный экстремум. Изопериметрическая задача. Необходимое условие.

Требуется найти экстремум функционала при условии, что другой функционал имеет заданное значение . Предполагается, что функционалы и дифференцируемы в рассматриваемом банаховом пространстве.

Лемма 1.

Если функционал достигает экстремума в точке при условии и не является экстремалью функционала , то для любого , удовл.

, , , .

По условию леммы

Так как - точка условного экстремума для функционала , то достигает экстремума в точке при условии .

По определению производная Гато

по теореме о существовании неявной функции , причем , .

Получаем имеет экстремум при .

Лемма 2.

Если линейный функционал обращается в ноль на тех же элементах, на которых обращается в ноль линейный функционал , то существует: .

Если , то утверждение леммы очевидно.

Если , то .

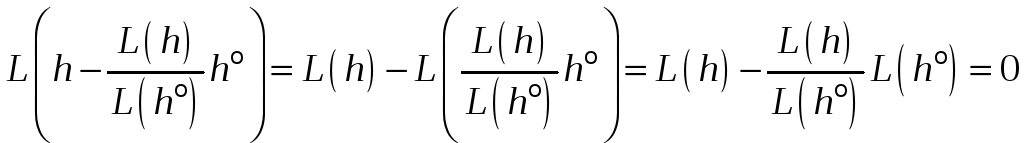
По условию:

где .

Теорема 1 (Эйлера).

Пусть кривая реализует экстремум функционала при условии , причем не является экстремалью , и и дифференцируемы в точке , тогда является экстремалью .

Доказательство.

Из условий теоремы следует, что при любом допустимом приращении . Кроме того, функционалы дифференцируемы является экстремалью .

Таким образом, чтобы решить изопериметрическую задачу, нужно найти общее решение уравнения Эйлера для функционала , где произвольные постоянные и параметр определяются из граничных условий и условий связи .

Теорема 2.

Если реализует экстремум дифференцируемого функционала в точке при условии , причем не является экстремалью ни одного из , и линейно независимы, то является экстремалью следующего функционала: (без доказательства).

Пример (задача Дидоны).

- при условии .

(первый интеграл интеграл уравнения Эйлера (интеграл энергии))

- дуга окружности

Проходит через точки , . Длина дуги равна , .

БИЛЕТ 10. Представление аналитической в круге функции рядом Тейлора. Нули аналитической функции.

Теорема.

Пусть аналитична при , тогда представима рядом Тейлора.

при

Доказательство:

Рассмотрим , тогда

По интегральной формуле Коши: .

Рассмотрим

.

Тогда подставим разложение в наш интеграл:

,

где - коэффициенты ряда Тейлора.

формула Вейерштрасса-Коши

Так как , , то

где .

Замечание 1:

То есть

3°. Нули аналитичной функции.

Определение: Если аналитична в , то точка называется нулем аналитичной функции кратности , если , то есть

Замечание 2:

- ноль кратности , , так как

Пример:

1)- ноль кратности 1.

2) - ноль кратности 4.

БИЛЕТ 11. Представление аналитической в кольце функции рядом Лорана.

Теорема:

Пусть аналитична при , тогда , где

.

Доказательство:

Рассмотрим , тогда . По интегральной формуле Коши . Знак минус потому что направление обхода против часовой стрелки.

1). , где , но , так как не определена в точке .

2).

, причем этот ряд сходится равномерно.

Подставим в интеграл:

.

Таким образом

,

где

- регулярная часть

- главная часть.

При

При

Лемма. (О единственности разложения ряда Лорана)

Пусть сходится при , тогда аналитична при и , .

Доказательство:

1). При сходится равномерно. (это простое следствие теоремы Абеля). По теореме Вейерштрасса функция аналитична в .

2). Вычислим

.

Так как

БИЛЕТ 16. Преобразование Лапласа: определение, свойства.

Пусть функция действительного переменного определена при (комплексно-значная функция). Тогда (1), где - комплексное число.

Функция удовлетворяет следующим свойствам:

1. Функция на любом конечном интервале непрерывна, за исключением, быть может, конечного числа точек разрыва 1-го рода.

2. Функция при .

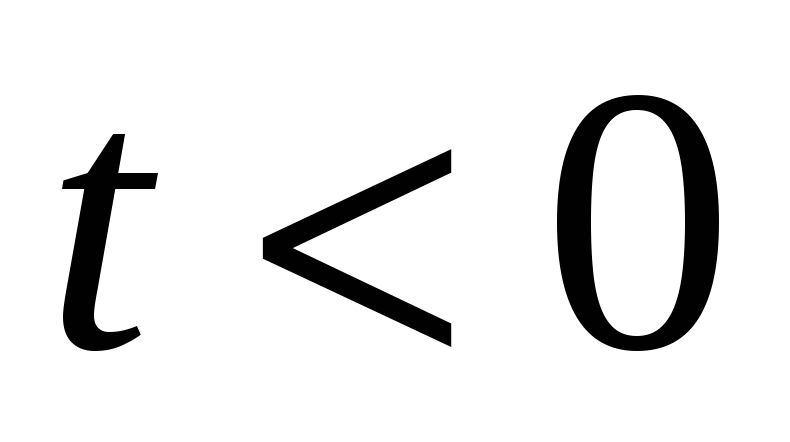3. Функция растет при 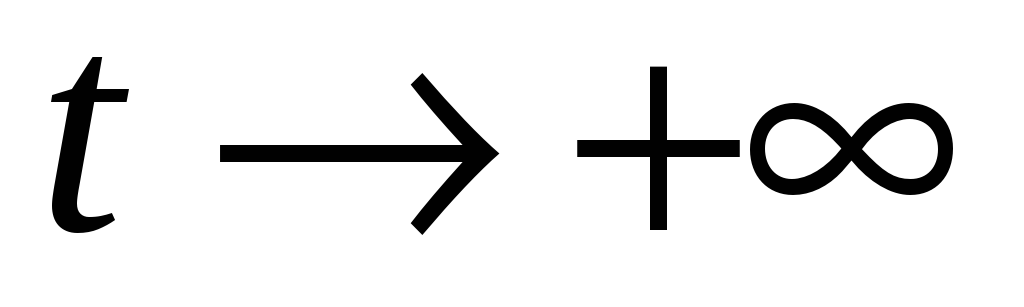не быстрее показательной функции (не быстрее экспоненты), то есть (2).

Точная нижняя грань чисел , входящих в формулу (2), называется показателем роста функции и обозначается .

Пример.

функция Хевисайда.

удовлетворяет трём выше написанным условиям.

(3)

Для функции Хевисайда: , .

Функцию , удовлетворяющую трём свойствам, будем называть оригиналом, а - изображением.

Начиная с этого момента и далее значок «» эквивалентен значку « »

или (так обозначается соответствие между оригиналом и изображением).

(3’).

Введем функцию , которая удовлетворяет условиям 1 и 3, но не удовлетворяет условию 2.

. Такая функция удовлетворяет условию 2.

Функции , удовлетворяют трем условиям. Для упрощения записи мы не будем писать функцию Хевисайда , но будем подразумевать, что функции , при .

Формулу (3’) можем записать так: .

Пример.

. Найти преобразование Лапласа, если - произвольное комплексное число.

.

А значит (4).

Очевидно, что данная функция будет аналитическая при .

Теорема (без доказательства).

Пусть - оригинал с показателем роста . Тогда изображение определено в полуплоскости и является аналитической функцией в этой полуплоскости.

Процесс нахождения по оригиналу изображения и обратное преобразование называется операционным исчислением.

Каждой функции соответствует единственное изображение : , но в некотором смысле обратное преобразование тоже единственно.

Теорема (единственности) (без доказательства).

Любое изображение однозначно определяет оригинал , кроме значений оригинала в точках разрыва.

2°. Свойства преобразования Лапласа.

1. Свойство линейности.

Если , а , , то .

Рассмотрим примеры.

Найдем преобразование Лапласа от тригонометрических и гиперболических функций.

Поскольку , то из формулы (4) вытекает:

,

2. Теорема подобия.

Если функция , - некоторая константа, то тогда .

Докажем это свойство.

Пусть . .

3. Дифференцирование оригиналов.

Пусть , кроме того, пусть или в более общем случае являются оригиналами.

Тогда (1).

(2).

Здесь , , где .

Докажем формулу (1).

Воспользуемся формулой интегрирования по частям:

{. Будем устремлять } . Формула (1) доказана.

4. Дифференцирование изображения.

(3).

Докажем эту формулу.

- аналитическая при .

.

Далее по индукции…

Примеры.

, , , , где - натуральное число.

Найдем изображения для этих функций.

.

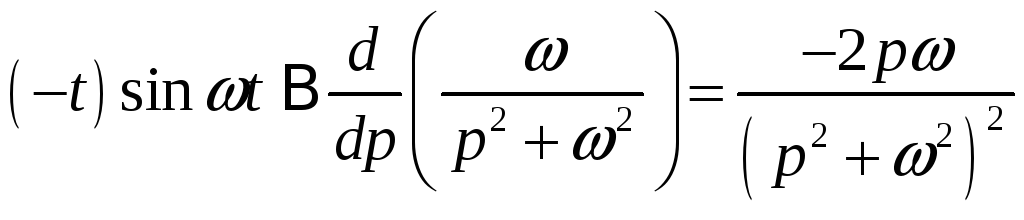
5. Интегрирование оригинала.

Пусть , тогда (4).

Если - оригинал, то можно легко проверить, что также является оригиналом. ,

Воспользуемся формулой (1). Пусть . Тогда по формуле (1)

, откуда вытекает формула (4).

6. Интегрирование изображения.

Пусть . Предположим, что функция является оригиналом.

Тогда (5).

Лемма.

Если - оригинал, то тогда .