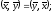Геометрические векторы.
Рассмотри
на плоскости 2 точки А и Б. По соединяющему
их от резку можно двигаться в обе стороны.
Если А – начало, а Б – конец, получим
направленный отрезок АБ, иначе БА.
Определение – геометрический вектор
– направленный отрезок который можно
перемещать параллельно самому себе.
Если у вектора совпадает начало и конец,
то вектор 0й. Длинной вектора вектора
будем называть величину соответствующей
направлению отрезка или расстояния
между нач. и конечными точками вектора
и обозначается – модуль(AB).
Если длинна вектора равна 1му, то
вектор-единичный. 2 вектора равны, если
они лежат на одной или на параллельных
прямых, направленных в одну сторону и
их длинны равны. 1й вектор имеющий
одинаковое направление с векротом АБ
– орт вектора АБ. Орт = (вектор АБ/длину
вектора). Угол между векторами А и Б –
угол С причем 0<C<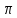 ,
при условии что А и Б имеют общее начало.
,
при условии что А и Б имеют общее начало.
Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов.
Скалярное произведение векторов – число которое находится по формуле |a|*|b|* cos(c), с – угол между векторами. Скалярное произведение (А,Б)=|а|*пр.а Б. = |Б|* пр.б. А.
Свойства скалярного произведения:
(а,б)=(б,а) тк cos(-c) = cos(c);
(а,б+с)= (а,б)+(а,с)
(α*а,б)=(а, α*б)= α(а,б)
(а,а)=|a|*|a| * cos(0) = |a|^2
Скалярное произведение |a|*|a|=0 только тогда, когда вектор а =0
Для того чтобы векторы а и б были ортогональны достаточно, чтобы их векторное произведение равнялось 0.
Скалярное произведение векторов в координатной форме
А{x1,y1,z1} B{x2,y2,z2}
(a,b)= x1x2+y1y2+z1z2
Док-во : рассмотрим 2 вектора в базисе ijk. А=x1i+y1j+z1k, b=x2i+y2j+z2k
(А,B) = (x1i+y1j+z1k, x2i+y2j+z2k)=x1x2(I,j) + x1y1(I,j)+x1z2(I,k)+y1x2(j,i)+y1y2(j,j)+y1z2(j,k)+z1x2(k,i)+z1y2(k,j)+z1z2(k1,k2) т.к i,j,k попарно ортогональны векторное произведение I,j,k = 0, а векторное произведение ijk вектора самого на себя = 1 получаем
(а,б)=x1x2+y1y2+z1z2
Векторное произведение векторов. В векторном произведении [a,b]=с
Такой
что 1) |c|=|a|*|b|*sin(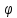 ),
2) вектор с ортогонален плоскости в
которой лежат вектора а и б. 3) вектора
а,б,с расположены таким образом, что из
конца вектора с кратчайший поворот от
вектора а к б виден против часовой
стрелки.(правая тройка векторов)
),
2) вектор с ортогонален плоскости в
которой лежат вектора а и б. 3) вектора
а,б,с расположены таким образом, что из
конца вектора с кратчайший поворот от
вектора а к б виден против часовой
стрелки.(правая тройка векторов)
Свойства векторного произведения:
[a,b]=-[b,a]
[a,b+c]=[a,b]+[a,c]
[a+b,c]=[a,c]+[b,c]
[
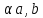 ]=
α[a,b]
]=
α[a,b][a,a]=0
Необходимость
и достаточность условия коллинеарности
векторов для того, чтобы а||б необходимо
и достаточно, чтобы векторное произведение
было равно 0. А||B
если их координаты пропорциональны
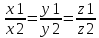 .
.
Геометрический смысл векторного произведения. |[a,b]|= площади параллелограмма, построенного на векторах а и б. Векторное произведение в координатной форме.
А={x1,y1,z1} b={x2,y2,z2}
[a,b]=
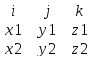 = определитель 3-го порядка вычисл. По
формуле:
= определитель 3-го порядка вычисл. По
формуле:
I*|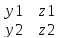 |
-J*|
|
-J*|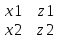 |
+K*|
|
+K*|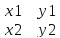 |
Получаем определители 2-го порядка,
которые вычисляются по формуле
(y1*z2-z1*y2)
получаем [a,b]={x3,y3,z3}
|
Получаем определители 2-го порядка,
которые вычисляются по формуле
(y1*z2-z1*y2)
получаем [a,b]={x3,y3,z3}
Смешенные произведения векторов
Смешенным произведением векторов называется число равное векторному произведению 2х векторов [a,b] скалярно умноженные на вектор c
([a,b],c)
Условие компланарности 3х векторов(лежат в одной плоскости) их смешенное произведение равно 0.Геометрический смысл смеш. Произв. – объем параллелепипеда построенного на векторах a,b,c численно равен их смешенному произведению. Смешенное произведение в координатной форме.
([a,b],c)=
| |
=x1*|
|
=x1*| |
-y1*|
|
-y1*|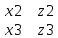 |+z1*
|
|+z1*
|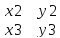 |
|
Плоскость и прямая в пространстве. Основные задачи о прямых и плоскостях.
Уравнение
плоскости α
проходящую через точку Мо перпендикулярн.
Вектору
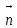 A(x-x0)+B(y-y0)+c(z-z0)=0
Мо{x0,y0,z0}
n{A,B,C}
M{x,y,z}
A(x-x0)+B(y-y0)+c(z-z0)=0
Мо{x0,y0,z0}
n{A,B,C}
M{x,y,z}
Полученное уравнение является (ММо,n) n-нормальный вектор перпендик к плоскости α. Преобразуем уравнение A(x-x0)+B(y-y0)+c(z-z0)=Ax-Axo+By-Byo+Cz-Czo=0 D=-Axo-Byo-Czo – число Ax+By+Cz+D=0(общее уравнение плоскости)
Угол
между плоскостями
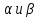 – угол, полученный при пересечении этих
плоскостей, причем 1 из углов будет равен
углу при пересечении нормальных векторовn1
и n2.
– угол, полученный при пересечении этих
плоскостей, причем 1 из углов будет равен
углу при пересечении нормальных векторовn1
и n2.
α: A1x+B1y+C1z+D1=0 n1={A1,B1,C1}
β: A2x+B2y+C2z+D2=0 n2={A2,B2,C2}
Из
скалярного произведения векторов
φ=arcos(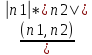 )
=
)
=
Уравнение плоскости, проходящую через 3 данные точки.
М1(x1,y1,z1); M2(x2,y2,z2); M3(x3,y3,z3)
Тогда произведение точка пространства с координатами x,y,z будет принадлежать плоскости когда M1M, M1M3, M1M2 будут компланарны, а значит их смешенное произведение будет равно 0. (M1M,[M1M3,M1M2])=0
M1M{x-x1;y-y1;z-z1}
M1M2{x2-x1;y2-y1;z2-z1}
M1M3{x3-x1;y3-y1;z3-z1}
α:
| |
Решаем уравнение, приравниваем к 0 и
получаем уравнение плоскости.
|
Решаем уравнение, приравниваем к 0 и
получаем уравнение плоскости.
Уравнение плоскости в отрезках.
Рассмотрим общее уравнение плоскости α, которое не проходит через начало координат, при этом D≠0
α:
Ax+By+Cz=
‑D|÷
(‑D)
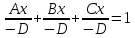 Вынесем в знаменательA,B,C
Вынесем в знаменательA,B,C
a=(-D/A),
b=(-D/B),
c=(-D/c)
 – уравнение плоскости α в отрезках
отсекаемых этой плоскостью от координатных
осей. Плоскость заданную таким образом
легко строить, т.к. она проходит через
точки (a;0;0),(0;b;0),
(0;0;c)
– уравнение плоскости α в отрезках
отсекаемых этой плоскостью от координатных
осей. Плоскость заданную таким образом
легко строить, т.к. она проходит через
точки (a;0;0),(0;b;0),
(0;0;c)
Уравнение плоскости проходящее через начало координат. D=0
Ax+Bx+Cx=0 Ax+By+D=0 –уравнение плоскости || OZ
N{0,0,1}, Ax+Cz+D=0 - || OY By+Cz+D=0 ||OX Ax+D=0 ||YOZ
Пример: найти расстояние от Мо {x,y,z} до плоскости α проходящей через точки М1{x1,y1,z1},М2{x2,y2,z2},М3{x3,y3,z3}. Для этого необходимо найти нормальный вектор n плоскости α, расстояние от Мо до α будет равен проекции ММо на n, т.е |MMo|*cos(β) β- угол между n и MMo. N=[M1M2,M1M3] (n,MMo)=|n|*|MMo|*cos(β).
Линия
в пространстве – как частный случай –
линия пересечения 2х плоскостей. Для
решения щадач неудобно использовать
общее уравнение прямой
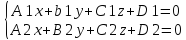
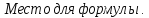
Каноническое уравнение прямой:
n1={A1,B1,C1} ǂǂ n2={A2,B2,C2}. Рассмотрим прямую D которая проходит через точку Мо{Xo,Yo,Zo}, которая принадлежит прямой D. A{l,m,n}-направляющий вектор прямой D. Тогда произвольная точка пространства M{x,y,z} будет принадлежать прямой D только тогда когда MoM||a.
MoM{x-xo;y-yo;z-zo}, если их координаты пропорциональны и
D=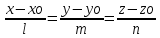
Параметрическое уравнение прямой:
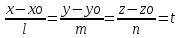
x=lt+xo y=yo+mt z=zo+nt ‑‑‑‑‑‑ параметрическое ур-е прямой.
Пример: составить каноническое уравнение прямой проходящ через 2 точки
М1(x1,y1,z1) M2(x2,y2,z2) ,берем любую из точек, лежащую на прямой к примеру М1, а за направляющий вектор возьмем вектор М1М2. Получим
 =t
Параметрическое уравнение прямой:
x=tx2-tx1+x1
=t
Параметрическое уравнение прямой:
x=tx2-tx1+x1
Y=ty2-ty1+y1, z=tz2-tz1+z1 Общее уравнение прямой: D-линия пересечения бесконечного множества плоскостей в том числе и следующих 2х.
(x-x1)/(x2-x1)=(y-y1)/(y2-y1) (x-x1)/(x2-x1)=(z-z1)/(z2-z1)
Подставив числа получим неполное уравнение плоскости. Одна или даже 2 координаты направляющего вектора прямой могут равняться 0, т.е. в каноническом уравнении в знаменателе может стоять 0, и это будет не деление на 0, а отношением к 0.
Составление
канонического уравнения прямой как
пересечение 2х плоскостей.

D=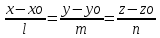 Любая прямая в пространстве пересекает
хотя бы одну координатную плоскость,
поэтому за точку прямой можно взять
точку пересечения данной плоскости и
и координатной плоскости приравняв
соответствующую координату к 0. Если
при этом получится система, которая не
имеет решений, значит данная прямая не
пересекает данную плоскость и следует
рассмотреть точку пересечения этой
прямой с какой-нибудь другой плоскостью.
Получим несколько точек лежащих на
данной прямой. Направляющий вектор
нашей прямой || последней следовательно
он || заданным плоскостям и перпендикулярен
нормальным векторам наших плоскостей,
а это значит что направляющий вектор
А=[n1,n2].
Находим произведение и подставляем в
уравнение D=
Любая прямая в пространстве пересекает
хотя бы одну координатную плоскость,
поэтому за точку прямой можно взять
точку пересечения данной плоскости и
и координатной плоскости приравняв
соответствующую координату к 0. Если
при этом получится система, которая не
имеет решений, значит данная прямая не
пересекает данную плоскость и следует
рассмотреть точку пересечения этой
прямой с какой-нибудь другой плоскостью.
Получим несколько точек лежащих на
данной прямой. Направляющий вектор
нашей прямой || последней следовательно
он || заданным плоскостям и перпендикулярен
нормальным векторам наших плоскостей,
а это значит что направляющий вектор
А=[n1,n2].
Находим произведение и подставляем в
уравнение D=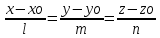
Найти Точку пересечения прямой D и плоскости α. Прямая пересекает плоскость в 1м месте, если направляющий вектор А, прямой D не перпендикулярен нормальному вектору n плоскости. (n,a)≠0, тогда есть точка пересечения. Для нахождения необходимо приравнять параметрическое уравнение прямой к уравнению плоскости.
Найти
координаты проекции в точке Р(1.0.1) на
плоскость
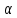 :
4x+6y+4z-25=0
:
4x+6y+4z-25=0
Проекция
P
есть точка пересечения прямой D
проходящей через точку Р и плоскость
α. Нормаль к
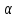 -
направляющий вектор прямойD.
Составляем параметрическое уравнение
прямой и решаем систему.
-
направляющий вектор прямойD.
Составляем параметрическое уравнение
прямой и решаем систему.
Найти
точку симметричную точке Р(1.-1.3)
относительно прямой d:
 Строим плоскость α, которой будет
принадлежать точка Р, причем α
перпендикулярнаd,
cледовательно
нормальный вектор к плоскости α равен
направляющему вектору прямой D.
N=a{1;-1;1}
ур-е плоскости
Строим плоскость α, которой будет
принадлежать точка Р, причем α
перпендикулярнаd,
cледовательно
нормальный вектор к плоскости α равен
направляющему вектору прямой D.
N=a{1;-1;1}
ур-е плоскости
1(x-0)-1(y+1)+1(z-3)=0 α: x-y+z-4=0 Теперь найдем точку пересечения прямой и плоскости приравняв уравнения прямой и плоскости. Q=(2;-1;1) Вектор PQ равен вектору P1Q Следовательно Q – середина PP1
X(q)=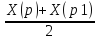 НаходимXp1
также для координат y
и z
и получаем точку симметричную данной
относительно прямой.
НаходимXp1
также для координат y
и z
и получаем точку симметричную данной
относительно прямой.
Взаимное расположение прямых в пространстве.
Прямые а || b если их направляющие векторы ||.
Найдем
расстояние от точки Мо(xo,yo,zo) до прямой
D
в пространстве. D=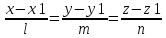 M1(x1,y1,z1)
a1||a
a1принадлежит
d
достроим до параллелограмма
М1Мо={xo-x1,yo-y1,z0-z1}
s=|[M1Mo,a]|
s=|a1|*h
M1(x1,y1,z1)
a1||a
a1принадлежит
d
достроим до параллелограмма
М1Мо={xo-x1,yo-y1,z0-z1}
s=|[M1Mo,a]|
s=|a1|*h
H=
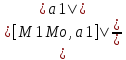
Расстояние между скрещивающимися прямыми.
А:
=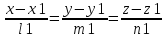 B:=
B:=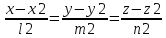
Их направляющие вектора равны a1 и a2
Возьмем 2 точки М1 на а и М2 на b M1M2={x2-x1;y2-y1;z2-z1}
H=

Определители n-го порядка. Вычисление и свойства.
n-порядок определяется в матрице по кол-ву строк и столбцов квадратной матрицы(число строк и столбцов равны). Определитель матрицы – это число, которое постоянно в соответствии целой таблице, т.е. матрицы.
Определитель 1го порядка равен элементу матрицы. Определитель 2го порядка – произведение главной диагонали – произведение побочной диагонали. Определитель 3го порядка: метод треугольн. Определитель не может быть разным у одной и той же матрици каким бы способом его не высчитывали.
Минором
какой-либо квадратной матрицы называется
определитель, полученный из матрицы
путем вычеркивания строки и столбца на
котором он находится
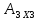 =
=
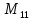 =
= и т.д.
и т.д.
Алгебраическим дополнением какого-либо элемента квадратной матрицы является минор этой матрицы, умноженный на (-1) в стпени №строки+№столбца на пересечении которых он находится.
Свойства определителей:
Определитель не поменяется, если матрицу транспонировать
Перестановка любых 2х строк или столбцов равносильна умножению определителя на -1.
Если в матрице 2 одинаковые строки или столбцы, то опред. = 0. Док-во, т.к. мы меняем местами одинак строки, то опред * на (-1), но строки не меняются, следоват-но определит. = 0.
Если каждый элемент какой-либо строки-столбца определителя умножить на действит число α, то это равносильно произведению всего определителя на число α .
Если в матрице есть 0вая строка или столбец, то опред=0
Если в матрице есть пропорциональные строки, то определитель = 0
Если каждый элемент какого-либо столбца(строки) матрицы представляет собой сумму 2х слагаемых, то определ. Можно представить в виде суммы 2х определителей.
Величина определителя не изменится, если к столбцу, строке прибавить другую стоку, столбец умноженное на действительное число α.
Величина определителя численно равна сумме элементов какой-либо строки или столбца, умноженное на свои алгебр. Дополнения. Разложение определителя по какой-либо строке или столбцу. Определители 4 и более высокого порядка можно вычислить только разложением по строке или столбцу. Перечисленные свойства справедливы для определителей любых порядков больше 1.
Пример
 = 4*
= 4* =0
=0
Для облегчения расчетов выбираем столб, где есть хотя бы один 0.
Определитель треугольной матрицы равен произведению элементов на главной диагонали или элементов на побочной диагонали умножен. На (-1) . Определитель диагональной матрицы равен произведению элементов стоящих на главной диагонали. Определитель AB равен определителю А умноженный на определитель B.Для нахождения определителя необходимо выделить строку или столбец где больше всего 0,далее как показано в примере сверху.
Матрица. Линейные операции с матрицами. Умножение матриц, обратная матрица.
Матрица
– таблица чисел, состоящая из m
строк и n
столбцов
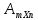
Под линейными операциями над матрицами понимают: сложение матриц, умножение матриц на любое действительное число. Для данных операций справедливо 8 аксиом:
A+B=B+A
A+(B+C)=(A+B)+C
A+θ=A
A+(-A)= θ
1*A=A
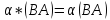
α(A+B)=αA+Αb
(α+β)A=αA+Βa
Умножение матриц. Для перемножения матриц необходимо чтобы кол-во столбцов у 1й матрицы = кол-ву строк у 2й матрицы. Матрица-строка умножается на матрицу столбец. Свойства умножения матриц:
1)A*B≠B*A 2) A*E(1я матрица)=E*A=A
3)A*(BC)=(AB)*C 4) A*(B+C)=AB+AC
5) (A+B)*C=AC+BC (матрицы умножаются строго по порядку)
Обратные
матрицы. Обр. матр. Называется вырожденной,
если ее определитель равен 0, в противном
случае невырожденной. Если С=AB
и определитель С=0, то матрица С-вырожденная
и хотя бы одна из А и B
тоже вырожденная. B
– обратная матрица к А, если справедливо
равенство AB=BA=E
и обозначается
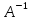 .
Теорема о существовании обратной
матрицы. Если матрица А невырожденная,
то у нее существует обратная матрица,
которая находится по формуле
.
Теорема о существовании обратной
матрицы. Если матрица А невырожденная,
то у нее существует обратная матрица,
которая находится по формуле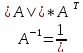 Матрица
Матрица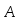 получается из матрицы А заменой каждого
элемента матрицы А его алгебраическим
дополнением. Теорема о единственности
обратной матрицы. Если матрица обратима,
то у нее существует только 1 обратная
матрица. Док-во: предоложим, что у матрицы
А есть 2 обратных матрицыB,C.
Тогда т.к. B
– обратная к А, следовательно AB=BA=E,
но с другой стороны AC=CA=E
Рассмотрим матрицу B=BE
по 5 свойству умножения матриц
B=BE=B(AC)=(BA)C=EC=C,что
противоречит свойству, следовательно
B=C.
Свойства
обратных матриц:
1)
получается из матрицы А заменой каждого
элемента матрицы А его алгебраическим
дополнением. Теорема о единственности
обратной матрицы. Если матрица обратима,
то у нее существует только 1 обратная
матрица. Док-во: предоложим, что у матрицы
А есть 2 обратных матрицыB,C.
Тогда т.к. B
– обратная к А, следовательно AB=BA=E,
но с другой стороны AC=CA=E
Рассмотрим матрицу B=BE
по 5 свойству умножения матриц
B=BE=B(AC)=(BA)C=EC=C,что
противоречит свойству, следовательно
B=C.
Свойства
обратных матриц:
1)
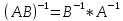 Док-во:
Док-во: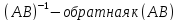 Докажем, что
Докажем, что *
*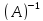 ‑ обратная к (AB)
(AB)(
‑ обратная к (AB)
(AB)(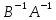 )=A(B
)=A(B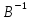 )
) =AE
=AE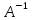 =E(
=E(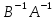 )(AB)=
)(AB)=
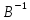 (
(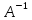 A)B=
A)B=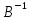 EB=
EB=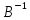 B=E
Следовательно
B=E
Следовательно
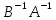 – обратная к (AB)
– обратная к (AB)
2)
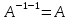 3) |
3) |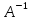 |=
|=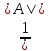 4) определитель транспонированной
матрицы
4) определитель транспонированной
матрицы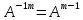 |(
|(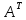 )|=
)|=
Элемнтарные преобразования матриц. Приведение к ступенчатому виду.
Эл. Преобразования: 1) перестановка местами любых 2х строк или столбцов матрицы. 2) Умножение любой строки или столбца на любое действ. Число не равное 0. В результате преобразований получается новая матрица эквивалентная данной, причем их определители равны.
Метод
гаусса, ранг матрицы. Матрица А порядка
MxN называется ступенчатой, если для
любых Аij=0
при i>j,
для любых i>r,
для любых Aii≠0
при i≤r
и r≥1,
r≤min(m,n)
Amxn= rg=1
Любую прямоугольную матрицу можно
привести к ступенчатому виду с помощью
элементарных преобразований путем
перестановки любых 2х строк, умножения
любой строки на число или сложения любых
2х строк. Способ приведения любой
прямоугольной матрицы к ступенчатой
форме-метод Гаусса.
rg=1
Любую прямоугольную матрицу можно
привести к ступенчатому виду с помощью
элементарных преобразований путем
перестановки любых 2х строк, умножения
любой строки на число или сложения любых
2х строк. Способ приведения любой
прямоугольной матрицы к ступенчатой
форме-метод Гаусса.
Пространство
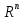 арифметических
векторов (линейное пространство).
арифметических
векторов (линейное пространство).
Множество
элементов x,y,z….![]() L
называется линейным пространством,
если для любых элементов x
и y
из L
и для любых α
L
называется линейным пространством,
если для любых элементов x
и y
из L
и для любых α![]() R
определены операции сложения элементов
и умножение элементов на число такие
что:
R
определены операции сложения элементов
и умножение элементов на число такие
что:
X+Y=Z
 L(действит
числа) 2) α*X=y
L(действит
числа) 2) α*X=y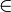 L
Примеры линейных пространств:
L
Примеры линейных пространств:
Множество действ чисел 2) множество геометрических векторов 3) множество матриц одного порядка 4) множество многочленов какой-либо степени и т.д.
N-мерным
арифметическим вектором называется
упорядоченная совокупность n-чисел(действит)
и записывается
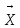 =(x1,x2,…,xn)
=(x1,x2,…,xn)
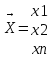 Для арифметических векторов справедливы
операции сложения векторов и умножение
вектора на число и аналогичные операции
с векторами. Геометрические векторы
можно рассматривать, как трехмерные
арифметические вектора, а пространство
геометрических векторов можно
рассматривать, как пространство 3х
мерных арифметических векторов.
Для арифметических векторов справедливы
операции сложения векторов и умножение
вектора на число и аналогичные операции
с векторами. Геометрические векторы
можно рассматривать, как трехмерные
арифметические вектора, а пространство
геометрических векторов можно
рассматривать, как пространство 3х
мерных арифметических векторов.
Рассмотрим линейное пространство L для него справедливы 8 аксиом, удовлетворяющие введенным в пространстве L операций сложения элементов и умножения элементов на число.
1)
x+y=y+x
2) x+(y+z)=(x+y)+z
3) x+θ=x
4)
![]() x
x![]() L,
L,
![]() (-x)
(-x)![]() L
5) 1*x=x
6)
L
5) 1*x=x
6)
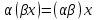 7)
7)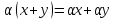 Элементы
линейного пространства принято называть
векторами. Пространство- векторное
линейное пространство.
Элементы
линейного пространства принято называть
векторами. Пространство- векторное
линейное пространство.
Линейная зависимость. Базис. Линейное пространство в
 (линейного
пространства)
(линейного
пространства)
Линейно
зависимые и линейно независимые системы
векторов. Опр. Система векторов (e1,e2,…ek
)![]() L
называется линейно зависимой, если
найдутся числа α1,α2,…αk
L
называется линейно зависимой, если
найдутся числа α1,α2,…αk
![]() R
действительные, причем не все равные
0, чтобы выполнялось равенство(α1e1+α2e2+…+αkek=0)
Если же данное равенство выполняется,
когда α1,α2,…αk=0
, тогда система векторов e1,e2,…ek
называется линейно независимой. Опр.
Если произвольный вектор X
из L
можно записать в виде равенства
x=x1e1+x2e2+…+xken,
где Xk
R
действительные, причем не все равные
0, чтобы выполнялось равенство(α1e1+α2e2+…+αkek=0)
Если же данное равенство выполняется,
когда α1,α2,…αk=0
, тогда система векторов e1,e2,…ek
называется линейно независимой. Опр.
Если произвольный вектор X
из L
можно записать в виде равенства
x=x1e1+x2e2+…+xken,
где Xk
![]() R
то говорят, что x
является линейной комбинацией векторов
(e1,e2,…ek
)
R
то говорят, что x
является линейной комбинацией векторов
(e1,e2,…ek
)![]() L
L
Теорема
необходимое и достаточное условие
линейной зависимости системы векторов.
Для того, чтобы система векторов
(e1,e2,…ek
)![]() L
была линейно зависимой необходимо и
достаточно, чтобы хотя бы 1 из векторов
системы можно было бы представить в
виде линейной комбинации остальных
векторов этой системы. Доказательство.
Необходимость. Пусть (e1,e2,…ek
)линейно
зависимые. Докажем, что при этом хотя
бы 1 из векторов можно представить в
виде линейной комбинации остальных
векторов этой системы. Из определения
ЛЗ системы следует что Ǝ α1,α2,…αk
L
была линейно зависимой необходимо и
достаточно, чтобы хотя бы 1 из векторов
системы можно было бы представить в
виде линейной комбинации остальных
векторов этой системы. Доказательство.
Необходимость. Пусть (e1,e2,…ek
)линейно
зависимые. Докажем, что при этом хотя
бы 1 из векторов можно представить в
виде линейной комбинации остальных
векторов этой системы. Из определения
ЛЗ системы следует что Ǝ α1,α2,…αk
![]() R
И все α≠0
α1e1+α2e2+…+αkek=0|÷αk,
которая не равна 0.
R
И все α≠0
α1e1+α2e2+…+αkek=0|÷αk,
которая не равна 0.
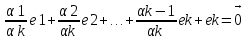 Достаточность: Пусть 1 из векоров
системы можно представить в виде лин.
Комбинации остальных векторов системы.
Тогда докажем, что система линейно
зависимая. Пусть для определенияek
является линейной комбинацией остальных
векторов системы. Тогда для него найдутся
числа
Достаточность: Пусть 1 из векоров
системы можно представить в виде лин.
Комбинации остальных векторов системы.
Тогда докажем, что система линейно
зависимая. Пусть для определенияek
является линейной комбинацией остальных
векторов системы. Тогда для него найдутся
числа
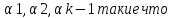 ek=
ek=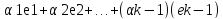
 +(‑
1)*ek=
+(‑
1)*ek=
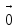 А значит αk=-1≠0
А это значит, что не все α1, α2, αk
равны 0. Это значит что система линейно
зависимая ч.т.д.
А значит αk=-1≠0
А это значит, что не все α1, α2, αk
равны 0. Это значит что система линейно
зависимая ч.т.д.
Свойства линейно зависимых и линейно независимых систем векторов:
1)
Любая система содержащая
 линейно зависимая. 2) любая система
содержащая 2 равных вектора линейно
зависимая. 3) Любая система, содержащая
2 взаимно противоположных вектора
линейно зависимая.
линейно зависимая. 2) любая система
содержащая 2 равных вектора линейно
зависимая. 3) Любая система, содержащая
2 взаимно противоположных вектора
линейно зависимая.
Базис
линейного пространства. Опред. Линейное
пространство L
называется n-мерным,
если в нем существует линейно-независимые
системы n
векторов, а любая система состоящая из
n+1
вектора линейно зависимая. В этом случае
число n
называется размерностью линейного
пространства L
и обозначается dimL=n
или
 .
Базисом линейного пространстваL
называется любая система из n
линейно-независимых векторов пространства
L,
причем любой вектор x
принадлежащий пространству L
может быть представлен в виде линейной
комбинации базисных векторов, т.е. если
система векторов (e1,e2,…,en)
из L
образует базис пространства L,
то любой вектор x
из L
можно представить в виде
.
Базисом линейного пространстваL
называется любая система из n
линейно-независимых векторов пространства
L,
причем любой вектор x
принадлежащий пространству L
может быть представлен в виде линейной
комбинации базисных векторов, т.е. если
система векторов (e1,e2,…,en)
из L
образует базис пространства L,
то любой вектор x
из L
можно представить в виде
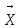 =α1e1+
α2e2+
α3e3+….+
αnen
‑‑‑‑‑‑ является
разложение вектора x
по базису e1,e2,en,
а действительные числа α1, α2,… αn
называются координатами вектора x
в базисе e1,e2,….,en.
=α1e1+
α2e2+
α3e3+….+
αnen
‑‑‑‑‑‑ является
разложение вектора x
по базису e1,e2,en,
а действительные числа α1, α2,… αn
называются координатами вектора x
в базисе e1,e2,….,en.
Теорема
в n
мерном пространстве L
существует базис из n
векторов. Без док-ва. Рассмотрим
арифметическое пространство
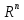 e1(1,0,0,…,0)
e2
(0,1,0,…0) e3
(0,0,1,..,0) en
(0,0,0,…,0,1 ) Данная система линейно
независимая, т.к. чтобы α1e1+
α2e2+
α3e3=0
равенство выполнялось каждое α должно
быть равно 0. Причем любой вектор x
принадлежащий пространству
e1(1,0,0,…,0)
e2
(0,1,0,…0) e3
(0,0,1,..,0) en
(0,0,0,…,0,1 ) Данная система линейно
независимая, т.к. чтобы α1e1+
α2e2+
α3e3=0
равенство выполнялось каждое α должно
быть равно 0. Причем любой вектор x
принадлежащий пространству
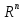 можно представить в виде линейной
комбинации (e1,e2,…,en)
т.к. вектор x=(x1,x2,x3…xn)=(
x1e1,x2e2,x3e3,…,xnen)
из определения операций сложения
векторов и умножения вектора на число.
Поэтому система векторов e1,e2,…,en
образует базис в пространстве en,
который будем называть естественным
базисом пространства
можно представить в виде линейной
комбинации (e1,e2,…,en)
т.к. вектор x=(x1,x2,x3…xn)=(
x1e1,x2e2,x3e3,…,xnen)
из определения операций сложения
векторов и умножения вектора на число.
Поэтому система векторов e1,e2,…,en
образует базис в пространстве en,
который будем называть естественным
базисом пространства
 ,
а действительные числаx1,x2,…,xn
координатами вектора x
в естественном базисе.
,
а действительные числаx1,x2,…,xn
координатами вектора x
в естественном базисе.
Теорема
о единственности разложения вектора
по базису. Если система векторов
e1,e2,…,en
образует базис в пространстве
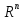 может быть единственным образом
представлен в видеx=(
c1e1+c2e2+c3e3..+..cnen)
где все с принадлежат R.
Док-во от противного. Пусть существует
2 различных вектора x
по базису en.
x
=( c1e1+c2e2+c3e3..+..cnen)
x=(
b1e1+b2e2+b3e3..+..bnen)
bi=ci
Причем все Сn=Bn,
Приравниваем уравнения и получается
(c1-b1)e1+(c2-b2)+..+(cn-bn)en=вектор
0. Но т.к. система векторов en
образует базис в системе векторов то
по определению базиса en,
система линейно независимая следовательно
равенство выполняется только тогда,
когда система линейно зависимая,
следовательно разложение вектора по
базису единственно. Ч.т.д.
может быть единственным образом
представлен в видеx=(
c1e1+c2e2+c3e3..+..cnen)
где все с принадлежат R.
Док-во от противного. Пусть существует
2 различных вектора x
по базису en.
x
=( c1e1+c2e2+c3e3..+..cnen)
x=(
b1e1+b2e2+b3e3..+..bnen)
bi=ci
Причем все Сn=Bn,
Приравниваем уравнения и получается
(c1-b1)e1+(c2-b2)+..+(cn-bn)en=вектор
0. Но т.к. система векторов en
образует базис в системе векторов то
по определению базиса en,
система линейно независимая следовательно
равенство выполняется только тогда,
когда система линейно зависимая,
следовательно разложение вектора по
базису единственно. Ч.т.д.
Подпространство
линейного пространства
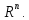 МножествоL
элементов из
МножествоL
элементов из
 называется линейным подпространством
линейного пространства
называется линейным подпространством
линейного пространства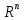 ,
если для любых векторовx,y
,
если для любых векторовx,y
![]() L
и для любых α
L
и для любых α![]() R
выполняется условие 1) x+y
R
выполняется условие 1) x+y![]() L
2)αx≤L
Другими словами множество L
из
L
2)αx≤L
Другими словами множество L
из
 является линейным подпространством
линейного пространстваL,
если множество L
само является линейным пространством,
относительно лин. Операций введенных
в линейном пространстве
является линейным подпространством
линейного пространстваL,
если множество L
само является линейным пространством,
относительно лин. Операций введенных
в линейном пространстве
 Пример. Рассмотрим множествоL,
арифметических векторов пространства
Пример. Рассмотрим множествоL,
арифметических векторов пространства
 таких, что последняя координата векторов
равна 0. Для любыхx(x1,x2,…,xn-1,0)
таких, что последняя координата векторов
равна 0. Для любыхx(x1,x2,…,xn-1,0)
![]() L
L
![]()
 .
Для любыхx,y
.
Для любыхx,y![]() L
и для любых α
L
и для любых α![]() R.
1) x+y=(x1+y1,x2+y2,…,xn-1+yn-1,0) 2)αx=(
αx1,
αx2,…,
αxn-1,0)
R.
1) x+y=(x1+y1,x2+y2,…,xn-1+yn-1,0) 2)αx=(
αx1,
αx2,…,
αxn-1,0)
![]() L
Следовательно
L-лин.
Подпространство линейного пространства
L
Следовательно
L-лин.
Подпространство линейного пространства
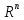 .
Линейное пространство
.
Линейное пространство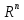 само является линейным подпространством
линейного пространства
само является линейным подпространством
линейного пространства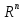 .
.
Билет 9 Размерность линейного подпространства. Ранг матрицы.
Определение. Число k называется размерностью линейного подпространства L, если в L существует система из k линейно независимых векторов, а любые k+1 вектора — линейно зависимы. Обозначаем dimL=k.
Нетрудно доказать следующее утверждение.
Теорема. В k-мерном линейном подпространстве существует базис их k векторов.
Доказательство
теоремы.
Действительно, если dimL=k,
то существует система из k
линейно независимых векторов
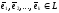 ,
а любая система из k+1
вектора
,
а любая система из k+1
вектора
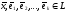 — линейно
зависима, но тогда любой вектор
— линейно
зависима, но тогда любой вектор
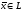 линейно выражается через векторы :
линейно выражается через векторы :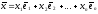 ,
т.е.
,
т.е.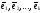 — базис в
L.
— базис в
L.
Справедливы также следующие утверждения (оставим их без доказательства).
Теорема. Любая упорядоченная система из k линейно независимых векторов k-мерного линейного подпространства является базисом в этом подпространстве.
Теорема. Размерность линейного подпространства равна числу векторов в базисе этого подпространства.
Отсюда следует: dim(Rn) = n.
Действительно, в пространстве Rn есть базис из n векторов — естественный базис в Rn.
Пример. Размерность линейного подпространства L арифметических векторов из Rn, у которых последние компоненты — нулевые, равна n – 1.
Действительно,
векторы
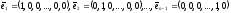 — очевидно, принадлежатL
и линейно
независимы. Покажем, что они образуют
базис в L.
Для произвольного вектора
— очевидно, принадлежатL
и линейно
независимы. Покажем, что они образуют
базис в L.
Для произвольного вектора
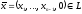 имеет место разложение справедливо:
имеет место разложение справедливо: ,
т.е. векторы
,
т.е. векторы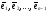 образуют
базис в L.
В этом базисе n-1
вектор, следовательно, dimL
= n
–1.
образуют
базис в L.
В этом базисе n-1
вектор, следовательно, dimL
= n
–1.
Тогда можно использовать другое определение базиса.
Определение. Любая упорядоченная линейно независимая система из k векторов k-мерного линейного подпространства L образует базис этого линейного подпространства L.
Это
означает, что если
dimL=k
и арифметические
векторы
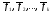 из
L
линейно
независимы, то для любого
из
L
линейно
независимы, то для любого
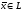 существуетединственный
набор чисел
существуетединственный
набор чисел
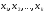 таких, что
таких, что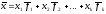 .
.
Подпространство строк и подпространство столбцов прямоугольной матрицы
Рассмотрим прямоугольную матрицу Am, n, у которой m строк и n столбцов:
 .
.
Её
строки —
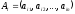 —являются векторами изRn,
—являются векторами изRn,
А
столбцы —
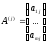 — являются векторами изRm.
— являются векторами изRm.
Понятно, что множество строк матрицы Am, n , к которому добавили все строки, которые могут быть получены при элементарных преобразованиях матрицы (исключая транспонирование) — линейное подпространство в Rn.
А аналогично образованное множество столбцов — линейное подпространство в Rm.
Это означает, что мы можем говорить о линейной зависимости и о линейной независимости строк и столбцов матрицы, о размерности подпространства строк и подпространства столбцов матрицы, о базисах в соответствующих подпростьранствах.
Ранг матрицы
Определение. Ранг матрицы равен максимальному числу линейно независимых строк матрицы. Обозначаем RgA, rgA.
Т.е., если ранг матрицы равен r, то среди строк матрицы есть r линейно независимых строк, а любые r +1 строки — линейно зависимы.
Определение. Матрицы, имеющие одинаковый ранг, называются подобными.
Утверждение. Элементарные преобразования не меняют ранга матрицы.
Доказательство
утверждения. Пусть
Am,
n
— прямоугольная матрица и RgA
= r.
Не умаляя общности, положим — линейно
независимы первые r
строк:
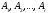 .
Выполним элементарные преобразования
строк матрицы. Обозначим полученную
матрицуA’,
ее строки —
.
Выполним элементарные преобразования
строк матрицы. Обозначим полученную
матрицуA’,
ее строки —
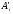 .Очевидно, что перестановка строк или
умножение строки на число не может
повлиять на количество линейно независимых
строк.
.Очевидно, что перестановка строк или
умножение строки на число не может
повлиять на количество линейно независимых
строк.
Выполним такое преобразование: к одной из строк матрицы прибавим другую, умноженную на отличное от нуля число.
Сначала выполним такое преобразование с первыми r линейно независимыми строками.
Например,
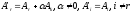 .
Тогда
.
Тогда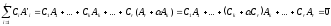
Т.к.
строки
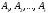 ,
то линейная комбинация равна нулю тогда
и только тогда, когда
,
то линейная комбинация равна нулю тогда
и только тогда, когда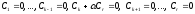 .
Отсюда немедленно следует, что и
.
Отсюда немедленно следует, что и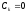 ,
т.е. первыеr
строк
преобразованной матрицы
,
т.е. первыеr
строк
преобразованной матрицы
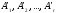 —
линейно независимы. Покажем, что любая
система
—
линейно независимы. Покажем, что любая
система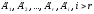 строк
преобразованной матрицы линейно
зависима, т.е. покажем, что строка
строк
преобразованной матрицы линейно
зависима, т.е. покажем, что строка линейно выражается через строки
линейно выражается через строки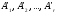 :
:
поскольку
строки
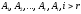 линейно зависимы, то
линейно зависимы, то
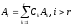 ,
а отсюда —
,
а отсюда —
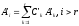 и
и
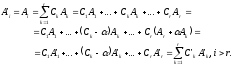
Если
же
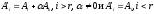 ,
то первыеr
строк
преобразованной матрицы линейно
независимы, а любые r+1
линейно
зависимы, т.к. любая строка преобразованной
матрицы линейно выражается через ее
первые r
линейно независимых строк:
,
то первыеr
строк
преобразованной матрицы линейно
независимы, а любые r+1
линейно
зависимы, т.к. любая строка преобразованной
матрицы линейно выражается через ее
первые r
линейно независимых строк:
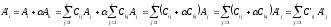
Утверждение доказано.
Теорема. Ранг матрицы равен числу ненулевых строк в ступенчатой форме матрицы.
Доказательство теоремы. Рассмотрим ступенчатую матрицу

т.е.
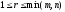 ,
,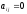 для
всех
для
всех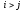 ,
и
,
и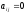 для
всех при
для
всех при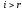 .
Важно понимать, то у ступенчатой матрицы
первыеr
диагональных
элементов
отличны от
нуля:
.
Важно понимать, то у ступенчатой матрицы
первыеr
диагональных
элементов
отличны от
нуля: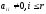 .
.
Первые
r
строк этой
матрицы линейно независимы. Действительно,
приравняем к нулю линейную комбинацию
этих строк:
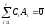 и вычислим ее в естественном базисе:
и вычислим ее в естественном базисе:
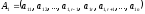 ,
,
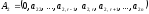 ,
…,
,
…,

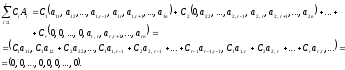
Равенство нулю линейной комбинации возможно тогда и только тогда, когда:
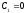 ,
поскольку
,
поскольку
 ,
,
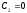 ,
поскольку
,
поскольку
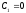 и
и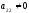 ,
…,
,
…,
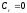 ,
поскольку
,
поскольку
 ,
,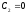 ,
…,
,
…,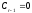 и
и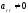 .
.
Итак, первые r ненулевые строки линейно независимы, а любые r+1 строки — линейно зависимы, т.к. линейно зависима любая система векторов, содержащая нулевой вектор.
Теорема доказана.
Отсюда — алгоритм вычисления ранга матрицы.
Приведем матрицу к ступенчатому виду (доказано, что это можно сделать гауссовым исключением), ранг исследуемой матрицы равен рангу ступенчатой матрицы (выше доказано, что элементарные преобразования не меняют ранга матрицы) , ранг ступенчатой матрицы равен числу ненулевых строк в ступенчатой форме матрицы (по только что доказанной теореме).
Билет № 10. Скалярное произведение в пространстве Rn, метрические соотношения.
Метрические соотношения в Rn
Определение.
Если
каждой паре векторов
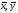 из
пространстваRn
поставлено
в соответствие действительное число
из
пространстваRn
поставлено
в соответствие действительное число
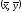 ,
так, что для любых
,
так, что для любых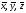 изRn
и любого действительного числа
изRn
и любого действительного числа
 справедливы следующие равенства:
справедливы следующие равенства:
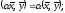
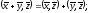
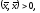 при
при
 ,
, ,
,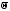 —
нулевой вектор,
—
нулевой вектор,
то
говорят, что в пространстве Rn
определено скалярное
произведение
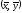 .
.
Пример. Легко проверить, что изученное в разделе «аналитическая геометрия» скалярное произведение известное из школьного курса скалярное произведение в трехмерном пространстве геометрических векторов (в R3) является скалярным произведением в определенном выше смысле.
Пример. Рассмотрим пространство арифметических векторов R2 ={X=(x1, x2)}. Определим скалярное произведение следующим образом:
(X, Y) = 2x1y1 + 3x2y2.
Легко убедиться, что для определенного таким образом скалярного произведения справедливы аксиомы 1. — 4.:
(X, Y) = 2x1y1 + 3x2y2 = 2y1x1 + 3y2x2 = (Y, X),
(X, Y) = 2(x1)y1 + 3(x2)y2 = (2y1x1 + 3y2x2) = (X, Y),
(X+Y, Z) = 2(x1+y1)z1 + 3(x2+y2)z2 = (2x1z1 + 3x2z2) + (2y1z1 + 3y2z2) = (X, Z) + (Y, Z),
(X,
X)
= 2x1x1
+ 3x2x2
= 2x12
+ 3x22
>0 если
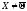 ,
если жеX
= (0, 0), то (X,
X)
= 0.
,
если жеX
= (0, 0), то (X,
X)
= 0.
Вернемся
к пространству арифметических векторов
Rn
= { }
}
Определим
в Rn
естественное
скалярное
произведение:
каждой паре векторов
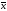 и
и из
этого пространства поставим в соответствие
действительное число
из
этого пространства поставим в соответствие
действительное число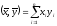 .
Нетрудно доказать, что для любых векторов
.
Нетрудно доказать, что для любых векторов ,
,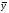 и
и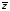 и
любого действительного числа
и
любого действительного числа для
для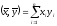 справедливо:
справедливо:

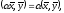
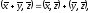
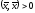 при
при
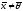 ,
и
,
и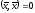 тогда и только тогда, когда
тогда и только тогда, когда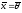 ,
,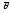 —
нулевой вектор.
—
нулевой вектор.
Пространство арифметических векторов Rn с определенным в нем естественным скалярным произведением называют евклидовым пространством арифметических векторов и иногда обозначают En.
Свойства скалярного произведения. Неравенство Коши-Буняковского
Теорема
(неравенство Коши-Буняковского).
Для любых векторов
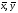 из
пространстваRn
справедливо
следующее неравенство
из
пространстваRn
справедливо
следующее неравенство
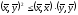 .
.
Доказательство
теоремы. Возьмем
произвольное число
 и рассмотрим
и рассмотрим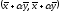 .
По последнему свойству скалярного
произведения для любых векторов
.
По последнему свойству скалярного
произведения для любых векторов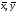 и
любого числа
и
любого числа справедливо:
справедливо: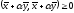 .
С другой стороны,
.
С другой стороны,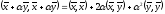 ,
т.е.
,
т.е.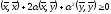 .
Выражение в левой части неравенства —
квадратный трехчлен относительно
.
Выражение в левой части неравенства —
квадратный трехчлен относительно .
Он неотрицателен тогда и только тогда,
когда дискриминант
.
Он неотрицателен тогда и только тогда,
когда дискриминант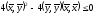 .
Из последнего неравенства немедленно
следует неравенство Коши-Буняковского:
.
Из последнего неравенства немедленно
следует неравенство Коши-Буняковского: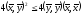 ,
, .
Теорема доказана.
.
Теорема доказана.
Метрические соотношения в Rn
Определение.
Число
 называется длиной вектора
называется длиной вектора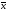 ;
число
;
число
 — расстоянием между векторами
— расстоянием между векторами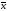 и
и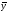 ;
угол
;
угол
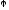 ,
косинус которого
,
косинус которого
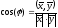 — углом между векторами
— углом между векторами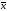 и
и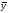 .
.
Если
в Rn
скалярное
произведение определено формулой
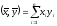 ,
то для любых
,
то для любых
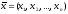 ,
,
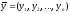 из Rn
справедливо:
из Rn
справедливо:
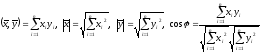
Ортогональность, ортогональные системы, ортонормированные базисы
Определение.
Векторы
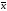 и
и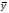 из
пространстваRn
называются ортогональными, если
из
пространстваRn
называются ортогональными, если
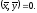
Определение.
Система
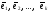 векторов из пространстваRn
называется ортогональной, если векторы
системы попарно ортогональны.
векторов из пространстваRn
называется ортогональной, если векторы
системы попарно ортогональны.
Теорема (о линейной независимости ортогональных систем). Ортогональная система векторов линейно независима.
Доказательство теоремы.
Предположим
противное: векторы
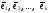 попарно
ортогональны, но они линейно зависимы.
Тогда один из векторов линейно выражается
через остальные. Например, пусть это
первый вектор:
попарно
ортогональны, но они линейно зависимы.
Тогда один из векторов линейно выражается
через остальные. Например, пусть это
первый вектор:
 ,
,
 (ясно, что речь идет о ненулевых векторах).
Тогда
(ясно, что речь идет о ненулевых векторах).
Тогда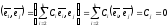 ,
для всехj
= 2,
3, …, k,
т.е.
,
для всехj
= 2,
3, …, k,
т.е.
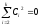 .
Полученное противоречие доказывает
теорему.
.
Полученное противоречие доказывает
теорему.
Определение.
Система
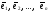 векторов
из пространстваRn
называется
ортонормированной, если векторы системы
попарно ортогональны и имеют единичную
длину.
векторов
из пространстваRn
называется
ортонормированной, если векторы системы
попарно ортогональны и имеют единичную
длину.
Определение. Базис пространства Rn называется ортонормированным базисом, если образующие его векторы попарно ортогональны и имеют единичную длину.
В
пространстве Rn
в
естественном скалярном произведении
 естественный
базис — ортонормированный базис.
естественный
базис — ортонормированный базис.
Билет №11
Система линейных алгебраических уравнений. Матричные уравнения.
Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида

Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными.
Составим матрицу А- матрица системы из коэфицентов при неизвестных (матрица)
Тогда исходную систему можно записать как матричное уравнение АХ=В
В том случае если число ур. = числу неизвестных m=n то матрич. Ур-ие АХ=В можно решить домножив обе части равенства на А^-1 слева!
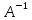 *А*Х=
*А*Х=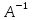 *В
*В
E*X=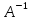 *В
*В
Х=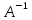 *В
*В
Если домножим на
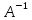 справа!
справа!
Х=В*
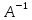
А*Х*В=С слева на
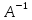 справа на
справа на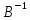
Х=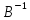 *С
*
*С
*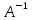
Если m не равно n то матричное уравнение решают другим способом
Билет №12
Системы n линейных алгебраических уравнений относительно n неизвестных. Правило Крамера.
Правило Крамера — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно).
Применяется для решения систем линейных уравнений у которых совпадает число неизвестных с числом уравнений.
Если в системе линейных уравнений с неизвестными (дельта не равно 0) , то система имеет решение и притом единственное. Это решение задается формулами
Х= и так же с остальными
и так же с остальными
Определитель
дельта равен

Определитель дельта1 получим из определителя дельта путем замены первого столбца определителя дельта (коэф. Прих1) на столбец свободных членов

Дельта Х2 получаем из определителя дельта путем замены второго столбца определителя дельта коэф при Х2 на столбец своб членов…..аналогично и для энного
Если дельта равна 0,то два случая
Дельта х1= дельта Х2=0---бесконечно много решений
Одно из них не равно нулю то системарешений не имеет
Билет №13
Свойства решений линейной системы. Нейтральная совместность единой системы. Совместность единой системы.
Если вектор x является решением однородной системы A·x = 0, то вектор αx также является решением этой системы. Здесь α — произвольное число.
Если векторы x и y являются решениями однородной системы A·x = 0, то вектор x + y также является решением этой системы.
Если вектор x является решением однородной системы A·x = 0, а вектор и y — решение неоднородной системы A·x = b, то вектор x + y является решением неоднородной системы A·x = b.
Если векторы x и y являются решениями неоднородной системы A·x = b, то вектор x − y является решением однородной системы A·x = 0.
Множество решений однородной линейной системы относительно n неизвестных является линейным подпространствомпространстваRn. Размерностьэтого подпространства равнаn − r, где r − рангматрицы системыA.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранграсширенной матрицы системы равен рангу матрицы системы.
Это утверждение называют теоремой Кронекера-Капелли.
Система линейных алгебраических уравнений
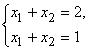
очевидно несовместна.
Ранги расширенной матрицы системы матрицы системы не равны, rank Ap = 2, rankA = 1, rank Ap ≠ rankA:
![]()
Билет №14