
- •Дисциплина «Физика» список литературы
- •Дополнительная
- •2. Учебные пособия
- •I. Учебная программа
- •Лекция №1
- •1. Современная картина строения физического мира.
- •1.5.Практическое использование элементарных частиц
- •1.1. Понятие о векторах и простейших действиях над ними
- •3.Метод размерных оценок в задачах физики
- •3.1. Введение в теорию размерных оценок. Преобразования подобия. Аффинные преобразования
- •3.2. Размерность и ее анализ. Алгоритм поиска размерных оценок
- •1.Размерность произвольной физической величины может быть лишь произведением степеней размерностей величин, принятых за основные.
- •2.Размерности обеих частей равенства, отражающего некоторую физическую закономерность, должны быть одинаковы.
- •3.3. Применение размерных оценок в механике. Примеры иллюстрации алгоритма для струны и маятника.
- •5. Мгновенная угловая скорость.
- •6. Связь линейной и угловой скоростей.
- •7. Модуль и направление углового ускорения.
- •8. Связь тангенциального и углового ускорения.
- •9. Мгновенное угловое ускорение.
- •5. Работа и энергия. Закон сохранения энергии
- •5.1. Работа и кинетическая энергия
- •5.2. Потенциальная энергия материальной точки во внешнем
- •5.3. О законе сохранения энергии и непотенциальных силах
- •5.4. Простые примеры
- •5.5. Равновесие и устойчивость
- •6.1. Особенности движения замкнутой системы из двух взаимодействующих материальных точек. Приведенная масса
- •6.2. Центр масс системы материальных точек
- •6.3. Потенциальная энергия взаимодействия. Закон сохранения
- •6.5. Упругие и неупругие соударения
- •Лекция 4
- •2. Избранные вопросы классической механики
- •2.1. Некоторые положения механики Ньютона.
- •2.2. Принципы механики Лагранжа.
- •2.3. Принцип Гамильтона.
- •7.1. Момент импульса и момент силы
- •7.3. Вращение абсолютно твердого тела вокруг неподвижной оси
- •Динамика твердого тела.
- •Свойства симметрии и законы сохранения. Сохранение энергии.
- •Сохранение импульса.
- •Сохранение момента импульса.
- •9.1. Принцип относительности Галилея
- •9.2. Законы механики в неинерциальных системах отсчета.
- •Некоторые задачи механики. Движение частицы в центральном поле сил.
- •2. Основные физические свойства и параметры жидкости. Силы и напряжения.
- •2.1. Плотность.
- •2.2. Вязкость.
- •2.3. Классификация сил.
- •2.3.1. Массовые силы.
- •2.3.2. Поверхностные силы.
- •2.3.3. Тензор напряжения.
- •8.3. Течение идеальной жидкости. Уравнение непрерывности
- •8.4. Архимедова сила. Уравнение Бернулли
- •8.5. Вязкость. Течение Пуазейля
- •1.4.1. Поток векторного поля.
- •2.3.4. Уравнение движения в напряжениях.
- •Уравнение Эйлера и Навье-Стока.
- •Специальная теория относительности.
- •10. Введение в релятивистскую механику
- •10.1. Постоянство скорости света для всех систем отсчета.
- •10.2. Следствия из преобразований Лоренца. Сокращение длины и замедление времени
- •10.3. Импульс и энергия в релятивистской механике
- •Относительность одновременности событий
- •Зависимость массы тела от скорости
- •Закон взаимосвязи массы и энергии
- •4.1.5. Релятивистская механика материальной точки
- •1.3. Фундаментальные взаимодействия
- •1.4. Стандартная модель и перспективы
- •1.1. Фермионы
- •1.2. Векторные бозоны
- •11.Элементарные частицы
- •11.1. Основные понятия и законы
- •11.1.1.Виды взаимодействий
- •11.1.2.Законы сохранения
- •11.2.Примеры решения задач
- •12.1. Основные свойства элементарных частиц.
- •12.2. Законы сохранения в микромире
- •12.3. Кварковая структура адронов
- •12.4. Электрослабое взаимодействие
- •Физика в конспективном изложении Содержание:
- •1. Вводные сведения - 6
- •Электричество – 49
- •9. Постоянное электрическое поле – 49
- •9.13.4.2. Теорема Гаусса для вектора - 78 10. Постоянный электрический ток – 79
- •10.7. Закон Ома для неоднородного участка цепи – 82 Магнетизм. Уравнения Максвелла – 83
- •11. Магнитное поле в вакууме – 83
- •11.11.3.1. Плотность энергии магнитного поля – 103 12. Магнитное поле в веществе – 103
- •Предисловие
- •1. Вводные сведения
- •1.1. Предсказание будущего - задача науки
- •1.2. Предмет физики
- •1.3. Физическая модель
- •1.4. Язык физики?
- •1.5. Экспериментальная и теоретическая физика
- •Физические основы механики
- •3.1.3. Абсолютно твердое тело
- •3.2. Тело отсчета
- •3.3. Система отсчета
- •3.4. Положение материальной точки в пространстве
- •3.10.1. Нормальное и тангенциальное ускорение
- •4. Динамика материальной точки
- •4.6.1. Система си (System international)
- •4.6.1.1. Размерность силы
- •5.3. Работа
- •5.6.1. Консервативность силы тяжести
- •5.6.2. Неконсервативность силы трения
- •5.7. Потенциальная энергия может быть введена только для поля консервативных сил
- •5.8.Закон сохранения механической энергии
- •6. Кинематика вращательного движения
- •6.1. Поступательное и вращательное движение
- •6.2. Псевдовектор бесконечно малого поворота
- •6.5. Связь линейной скорости материальной точки твердого тела и угловой скорости
- •8. Элементы специальной теории относительности
- •8.2. Принцип относительности Галилея:
- •8.3. Неудовлетворительность механики Ньютона при больших скоростях
- •8.5.1. Вывод преобразований Лоренца
- •8.6. Следствия из преобразований Лоренца
- •9.3. Электрическое поле
- •9.3.6. Принцип суперпозиции электрических полей
- •9.3.7. Напряженность поля точечного заряда
- •9.3.8. Линии напряженности
- •9.3.9. Линии напряженности точечных зарядов
- •9.4.4.1. Поле равномерно заряженной бесконечной плоскости
- •9.4.4.3. Поле однородно заряженного бесконечного цилиндра
- •9.9. Проводник в электрическом поле
- •9.10. Электроемкость уединенного проводника
- •9.11. Электроемкость конденсатора
- •9.12. Энергия электрического поля
- •9.12.1. Плотность энергии электрического поля в вакууме
- •9.13. Электрическое поле в диэлектрике
- •9.13.1. Диэлектрик?
- •9.13.1.1. Два типа диэлектриков - полярные и неполярные
- •9.13.2. Поляризованность диэлектрика (вектор поляризации) - это дипольный момент единицы объема:
- •9.13.4.1. Плотность энергии электрического поля в диэлектрике
- •10.4. Закон Ома для участка цепи
- •10.5. Закон Ома в дифференциальной форме
- •10.6. Закон Джоуля-Ленца в дифференциальной форме
- •Магнетизм. Уравнения Максвелла
- •11.5.6. Магнитное поле тороида
- •11.6. Закон Ампера
- •11.7. Сила Лоренца - это сила, действующая со стороны магнитного поля на движущийся в нем заряд
- •11.7.1. Движение заряженной частицы в однородном магнитном поле
- •11.8. Рамка с током в магнитном поле
- •11.11.1. Потокосцепление
- •11.11.2. Индуктивность соленоида
- •11.11.3. Энергия магнитного поля
- •12. Магнитное поле в веществе
- •12.2. Классификация магнетиков
- •13. Уравнения Максвелла
- •13.3. Система уравнений Максвелла в интегральной форме
- •13.4. Система уравнений Максвелла в дифференциальной форме
13. Уравнения Максвелла
Уравнения Максвелла выражают связи между характеристиками электромагнитного поля:
![]() -
(9.3.3)
,
(11.10.2.1);
-
(9.3.3)
,
(11.10.2.1);
![]() -(11.3);
-(11.3);
![]() -(9.13.4);
-(9.13.4);
![]() -(12.5).
-(12.5).
Сформулированы уравнения в 1861-1865 гг. Дж. К. Максвеллом на основе обобщения эмпирических законов электрических и магнитных явлений. Развивая идеи М. Фарадея, Максвелл впервые ввел точный термин "электромагнитное поле".
13.1. Первая пара уравнений Максвелла в интегральной форме

![]()
13.1.1. Первое уравнение первой пары - это закон Фарадея-Ленца
|
|
|
S - произвольная поверхность, "натянутая" на контур l. Это уравнение - обобщенная формулировка закона электромагнитной индукции (11.10). В самом деле:
значит
в (13.1.1)
справа стоит -
|
Левую
часть уравнения,
![]() ,
домножим и поделим на q - заряд пробной
частицы, помещенной в электрическое
поле :
,
домножим и поделим на q - заряд пробной
частицы, помещенной в электрическое
поле :
Мы получили закон Фарадея-Ленца (11.10.1) :
![]()
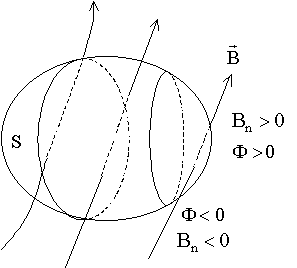
13.1.2. Второе уравнение первой пары - нет магнитных зарядов
|
|
|
Поток
вектора
|
13.2. Вторая пара уравнений Максвелла в интегральной форме

13.2.1. Первое уравнение второй пары - это теорема о циркуляции + что-то еще.
Для
вектора
![]() теорема
о циркуляции (11.5.4) гласит:
теорема
о циркуляции (11.5.4) гласит:
|
|
|
|
(11.5.4) |
В вакууме:
![]() .
.
Тогда
|
|
или |
|
При непрерывном распределении тока через поверхность S
![]() ,
,
здесь j - плотность тока (10.2). Тогда имеем
![]() .
.
Интеграл
слева берется по произвольному
воображаемому контуру, интеграл справа
- по произвольной поверхности, "натянутой"
на этот контур.
В веществе теорема о
циркуляции для вектора
![]() имеет
тот же вид:
имеет
тот же вид:
![]() ,
,
но при этом в интеграле справа не учитываются микроскопические токи вещества, приводящие к изменению магнитной индукции в веществе (12).
13.2.1.1. + что-то еще - это "ток смещения"
Применим
теорему о циркуляции вектора
![]() к
магнитному полю, созданному переменным
электрическим током, перезаряжающим
конденсатор.
к
магнитному полю, созданному переменным
электрическим током, перезаряжающим
конденсатор.

 ,
,
 .
.
См. (9.4.4.1) , (10.1), (10.2).
На
S2
j = 0, но
![]() ,
а по величине
,
а по величине![]() ,
значит ?
,
значит ?![]() .
.
Величину
 Максвелл
назвал"током
смещения".
Максвелл
назвал"током
смещения".
Как видно, "ток смещения" - это переменное во времени электрическое поле. Первое уравнение второй пары утверждает, что магнитное поле создается током проводимости и переменным электрическим полем ("током смещения").
13.2.2.
Второе уравнение второй пары
- это теорема Гаусса для вектора
![]() (9.13.4)
(9.13.4)
![]() ,
,
где qi - свободные, не связанные заряды.
При непрерывном распределении заряда
![]() .
.
13.3. Система уравнений Максвелла в интегральной форме
Первая пара (13.1)
|
|
|
|
|
|
|
|
Вторая пара (13.2)
|
|
|
|
|
|
|
|
13.4. Система уравнений Максвелла в дифференциальной форме
Применяя теорему Стокса можно преобразовать интеграл по замкнутому контуру l в интеграл по поверхности S, натянутой на этот контур.
Теорема Остроградского-Гаусса позволяет преобразовать интеграл по замкнутой поверхности S в интеграл по объему, ограниченному этой поверхностью. Преобразовав левые части уравнений (13.3) можно получить систему Максвелла в дифференциальной форме:
Первая пара:
|
|
|
|
|
|
|
|
Вторая пара:
|
|
|
|
|
|
|
|
Здесь
 .
.
К
этим уравнениям необходимо добавить
закон Ома в дифференциальной форме и
связь
![]() с
с![]() ,
,![]() с
с![]() :
:
|
|
|
см. (10.5), |
|
|
|
см. (9.13.4), |
|
|
|
см. (12.5). |
Эти три векторных уравнения характеризуют свойства среды. Семь записанных выше уравнений составляют основу электродинамики покоящихся сред.



 ,
, ,
, ,
, ,
,