7.3. Вращение абсолютно твердого тела вокруг неподвижной оси

Переходя к рассмотрению движения макроскопических тел, определим сначала наиболее простой тип движения, зависящего от геометрии тела. И первый шаг на этом пути — исключение из рассмотрения движения деформируемых тел, так как заранее очевидно, что движения многих частей тела друг относительно друга (и, соответственно, их математическое описание) могут быть достаточно сложны. Это означает, что мы начнем с изучения движения абсолютно твердых тел. Но и среди всевозможных движений абсолютно твердого тела мы выберем, по-возможности, наиболее простое. Дело в том, что для однозначного определения положения абсолютно твердого тела в пространстве необходимо задать шесть независимых величин — шесть степеней свободы. Мы же на данный момент ограничимся простейшим но практически важным случаем, когда существенна лишь одна степень свободы, — вращением абсолютно твердого тела вокруг неподвижной оси. При этом изменение положения тела в пространстве однозначно определяется единственной координатой φ— углом поворота тела вокруг оси.

Вывод основного уравнения для вращения тела вокруг неподвижной оси мы для наглядности проведем на примере вращения тонкого однородного диска вокруг вертикальной оси, перпендикулярной его поверхности и проходящей через его центр (рис. 7.8).

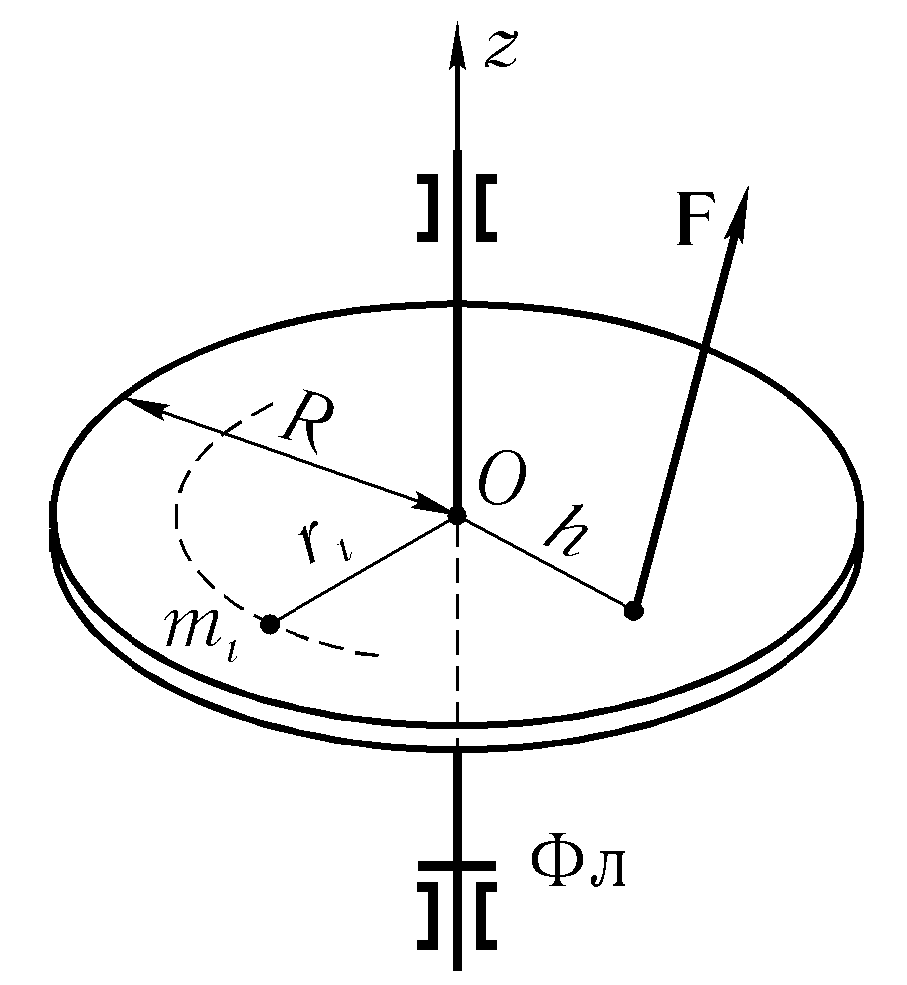
рис. 7.8. вращение тонкого однородного диска вокруг вертикальной оси, перпендикулярной его поверхности и проходящей через его центр

Слово «тонкий» означает, что толщина диска намного меньше его радиуса и что всеми эффектами, зависящими от толщины диска, можно пренебречь. Чтобы ствить такое вращение, диск жестко соединен с твердым стержнем, направленным вдоль оси Oz и

заключенным в подшипники. Опирающиеся на подшипники фланцы Фл, предотвращают перемещение диска в вертикальном направлении. Будем полагать, что масса и радиус стержня пренебрежимо малы по сравнению соответственно с массой и радиусом диска. Допустим также, что в некоторой точке расстоянии h от оси к диску приложена внешняя сила F, модуль и направление которой могут, вообще говоря, меняться со временем. Масса диска равна М, радиус диска — R.

Нашей целью является вывод уравнения движения диска, то есть уравнения, с помощью которого можно было бы находить функцию φ(t), которая

играет в данной задаче ту же роль, что и функция r(t) в задачах о движении материальной точки.

При выводе мы воспользуемся основным приемом, который применяется

в механике для изучения движения тел конечных размеров. Все тело мысленно разбивается на совокупность малых частичек, которые можно рассматривать как материальные точки, взаимодействующие друг с другом и с другими телами. В результате задача сводится к задаче о движении системы материальных точек, для которых справедливы все законы движения, рассмотренные в предыдущих разделах. Такой выделенный элемент макроскопического тела нередко называют физически бесконечно малым объемом, полагая, что все физические параметры внутри каждого из этих

объемов совершенно однородны, а взаимодействие существенно лишь с внешним окружением. (Математически эта идея выражается удержанием лишь первого члена ряда Тэйлора во всех функциональных зависимостях.)

Итак, разобъем мысленно наш диск на совокупность материальных точек

с массами m_iтак что ∑m_i= М. Мы уже отмечали, что при изучении вращательных движений целесообразно пользоваться не вторым законом Ньютона, но уравнением моментов. Для системы материальных точек уравнение для суммарного момента импульса L имеет вид

dL/dt =M_BH

где

L = ∑L_i,

a L_i— момент импульса i-той материальной точки системы относительно одного и того же центра О.

Выберем центр О в точке пересечения оси вращения с плоскостью диска.

Все образующие диск материальные точки будут при его вращении двигаться по окружностям с радиусами r_i, гдеr_i— модуль радиуса-вектора, соединяющего соответствующую i-ую материальную точку с центром О. Момент импульса отдельной материальной точки определяется векторным произведением:

L_i = [r_i р_i] = m_i[r_i v_i]

где р_i— импульс, av_i— скорость i-той материальной точки. Отсюда следуют две важные особенности нашей задачи. Во-первых, поскольку векторное произведение направлено перпендикулярно плоскости, в которой лежат образующие его векторы, то все моменты импульсаL_iнаправлены вдоль оси Oz, так как плоскость векторовr_iиv_iперпендикулярна этой оси. Это означает, что у суммарного момента импульса дискаLотлична от нуля только одна компонентаL_z= ∑L_iz. Во-вторых, при вращении диска все образующие его материальные точки движутся по окружностям, поэтомуr_iиv_i всегда перпендикулярны друг другу, синус угла между ними равен единице, и для L_izв соответствии с определением векторного произведения получаем

L_iz = m_ir_iv_i = m_ir_i²ω_i (7.12)

Мы учли, что

v_i = r_iω_i ,

где

ω= dφ/dt— угловая скорость вращения, одинаковая для всех точек диска. Знак L_izзависит от того, куда направлено векторное произведение [r v] — вдоль выбранного положительного направления оси Oz или против него. Мы выбрали для определенности знак «плюс».

Вернемся теперь к уравнению моментов. Левая часть этого уравнения для отличной от нуля компоненты L_z с учетом (7.12) принимает вид

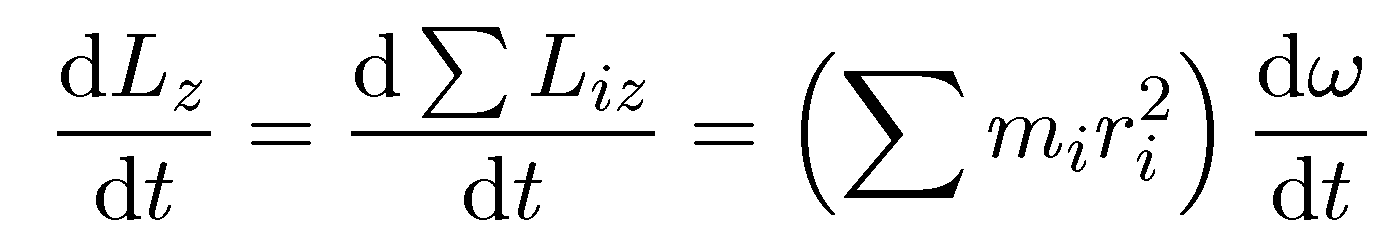(7.13)

Величина, равная сумме произведений элементарных масс на квадрат

их расстояний от некоторой оси Oz называется моментом инерции тела относительно данной оси:

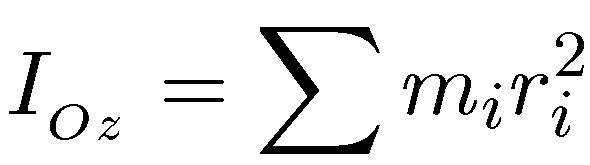
(7.14)

где суммирование производится по всем элементарным массам m_i, на которые мысленно разбито тело. Используя (7.12) и (7.14), выражение для

z-компоненты суммарного момента импульса диска можно записать в виде

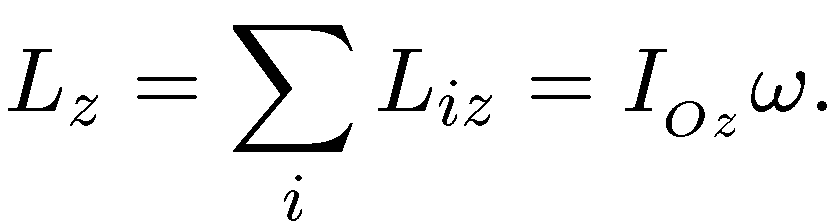
(7.15)

Таким образом, левая часть уравнения моментов может быть записана как

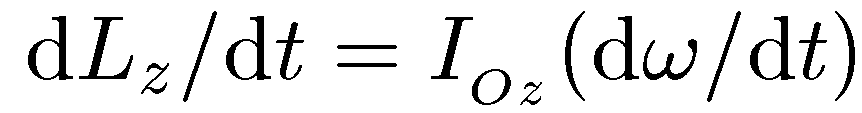
откуда, подставляя ω = dφ/dt, окончательно получаем

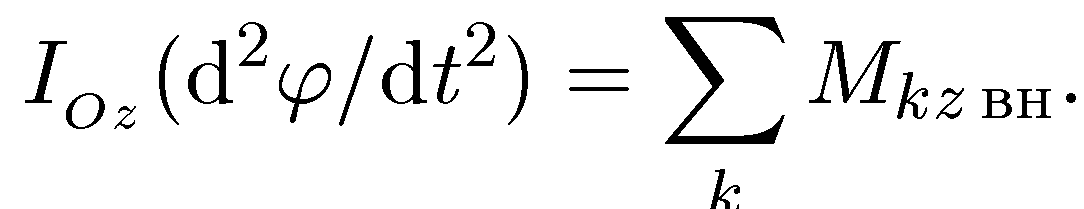
(7.16)

Сделаем одно замечание, касающееся принятой в механике терминологии.

Проекция вектора момента силы М на некоторую ось Oz, проходящую через центр О, относительно которого определен М, назывется моментом силы относительно оси Oz, который мы будем обозначать Моси. С учетом этого замечания уравнение(7.16) можно также представить в виде

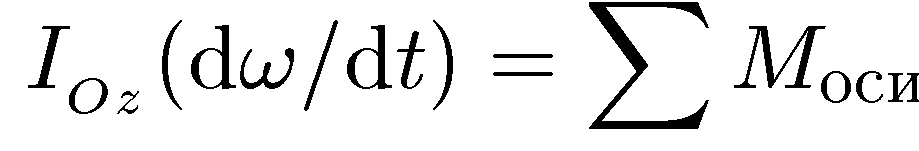
(7.17)

Хотя мы вывели уравнение (7.17) для частного случая (тонкого диска), этот вывод посредством интегрирования по слоям обобщается на случай вращения вокруг неподвижной оси тел любой формы.Итак, основное уравнение для вращения абсолютно твердого тела вокруг неподвижной оси Oz можно записать в виде

Как и второй закон Ньютона, оно является дифференциальным уравнением.

Нахождение из этого уравнения функции φ(t) — зависимости угла поворота тела от времени, решает одну из основных задач механики: предсказать положение движущегося тела в различные моменты времени при задании двух начальных условий: начального положения и скорости. В нашем случае начальные условия — это значение угла поворота в начальный момент времени, φ(0) = φ₀, и начальной угловой скорости ω(0) = ω₀. Значения φ₀ и ω₀определяютя условиями конкретной задачи. Таким образом, задание начальных условий является одним из важнейших элементов строгой математической постановки конкретной задачи о вращении твердого тела.

Характерной отличительной особенностью задачи о вращении тела вокруг оси по сравнению с задачей о движении материальной точки является то, что теперь в основное уравнение входит не масса m, а момент инерцииI_Oz, и не силаF, а момент силы относительно осиМ_0СИ.

Подчеркнем, что момент инерции тела относительно некоторой оси существует безотносительно к тому, вращается тело вокруг этой оси или покоится. Если же тело вращается вокруг некоторой оси под действием внешних сил, то момент инерции служит мерой инертности тела при вращении.

В самом деле, при одном и том же моменте внешних сил относительно оси вращения угловое ускорение будет меньше у того тела, у которого больше момент инерции. Таким образом, момент инерции тела при вращательном движении играет ту же роль меры инертности, что его масса при поступательном движении.

Как видно из определения (7.14), задание полной массы тела mеще ничего не говорит о величине его момента инерции I_Oz, который зависит от того, как расположены различные части тела (различные элементы его полной массы) относительно той или иной оси Oz, конкретное положение которой определяется условиями задачи. Поэтому при решении каждой конкретной задачи о вращении вопрос о величине I_Ozтребует отдельного рассмотрения.

Покажем на примере нашей исходной задачи о вращении тонкого диска, как

определяется момент инерции. Здесь нам необходимо найти момент инерции

однородного диска относительно оси, перпендикулярной к плоскости диска

и проходящей через его центр (рис. 7.8). Каждый из элементарных объемов

с массой m_i, на которые мы мысленно разбили весь диск, можно представить как произведение плотности тела ρ на соответствующий элементарный

объем ∆V_i.

m_i = ρ∆V_i

Следовательно, выражение (7.14) для момента инерции I_Ozможно представить в виде

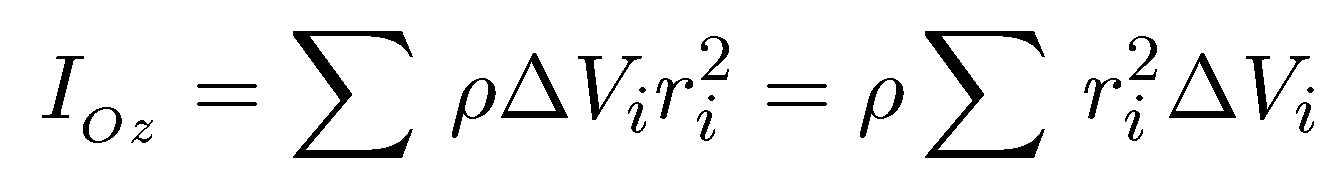
где мы учли, что для однородного диска плотность постоянна, и поэтому вынесли ρ за знак суммирования. При переходе к бесконечно малым значениям ∆V_iсуммирование сводится к интегрированию:

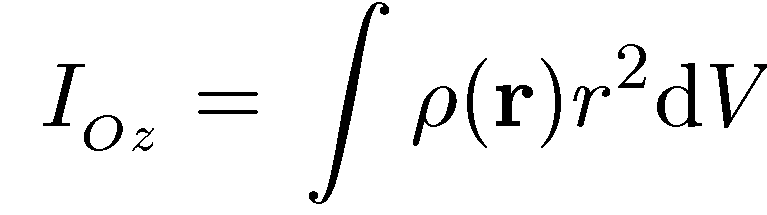
(7.18)

Ради большей общности результата мы вернули р(r) под знак интеграла.

Симметрия задачи подсказывает наиболее простой путь вычисления I_Ozв

случае однородного тела вращения. Разобьем наш диск на кольцевые слои

толщиной dr. Объем такого слоя равен

dV = b 2πr dr,

где b — толщина диска. Подставляя это выражение в (7.18), получаем

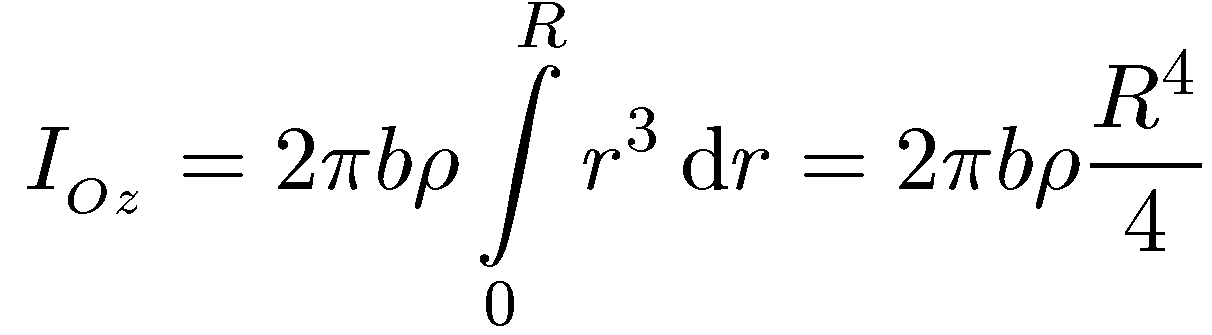
Последний результат можно выразить через полную массу диска m, равную

произведению плотности ρ на объем диска b πR². Окончательно получаем

I_oz =mR²/2. (7.19)

Нахождение момента инерции в рассмотренном примере сильно упрощалось тем, что тело было однородным и симметричным, а момент инерции мы вычисляли относительно оси симметрии. Если бы мы захотели найти момент инерции диска относительно, например, оси, перпендикулярной к диску и проходящей через его край, то вычисления оказались бы более сложными.

В подобных случаях нахождение момента инерции значительно облегчается, если воспользоваться следующей теоремой: «момент инерции I относительно произвольной оси равен сумме момента инерции I_С относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела т на квадрат расстояния а между осями», т. е.

I = I_с+mа².(7.20)

Что касается центра масс твердого тела, то он определяется по уже известному правилу

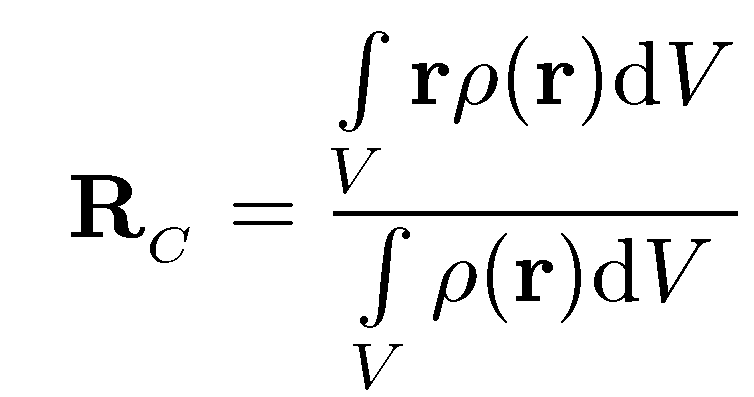
Для доказательства соотношения (7.20) предположим, что «старая» и «новая» оси связаны вектором параллельного переноса R(рис. 7.9):

r_i=r_i0+R,

где r_iиr_i0— старый и новый радиусы-векторы i-той точки в плоскости ее вращения. Тогда моменты инерции связаны следующим образом:

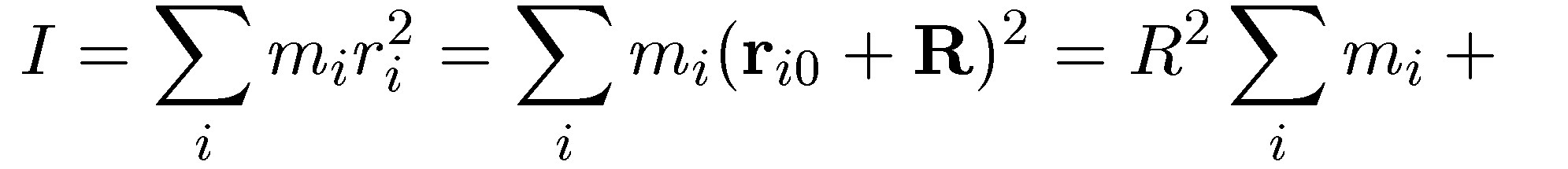
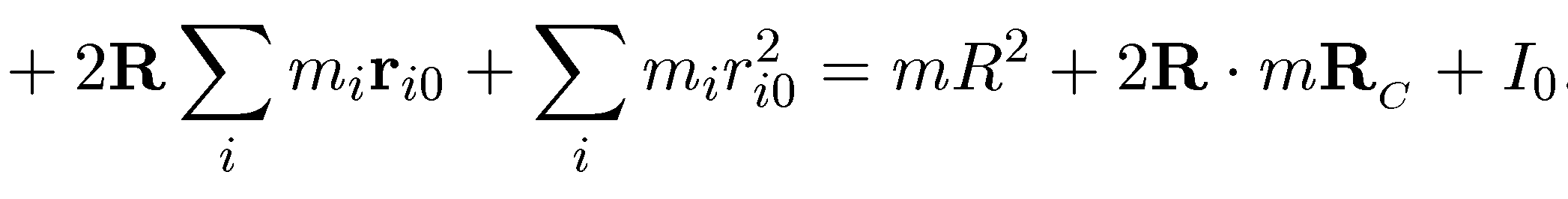
Если «старая» ось проходила через центр инерции, то R_c= 0, a I₀= I_c. Теорема доказана. Ее обычно называюттеоремой Штейнераили Гюйгенса-Штейнера. Отметим, что в ней отнюдь не предполагается какая-либо особая симметрия тела. В соответствии с названной теоремой, момент инерции диска относительно оси, перпендикулярной поверхности диска и проходящей через его край, равен найденному нами моменту инерции (7.19) относительно оси, проходящей через центр диска, плюсmR²(расстояние между осями

равно радиусу диска R):

В отличие от второго закона Ньютона, в правую часть уравнения вращательного движения входит не сила, а момент силы относительно оси. При этом он играет роль, аналогичную той, которую играет сила для поступательного движения.

В реальных задачах непосредственно сам момент силы обычно не задан, а заданы модули и направления внешних сил и точки приложения этих сил к телу, как, например, было в

нашей задаче о вращении тонкого диска (см. рис. 7.8).

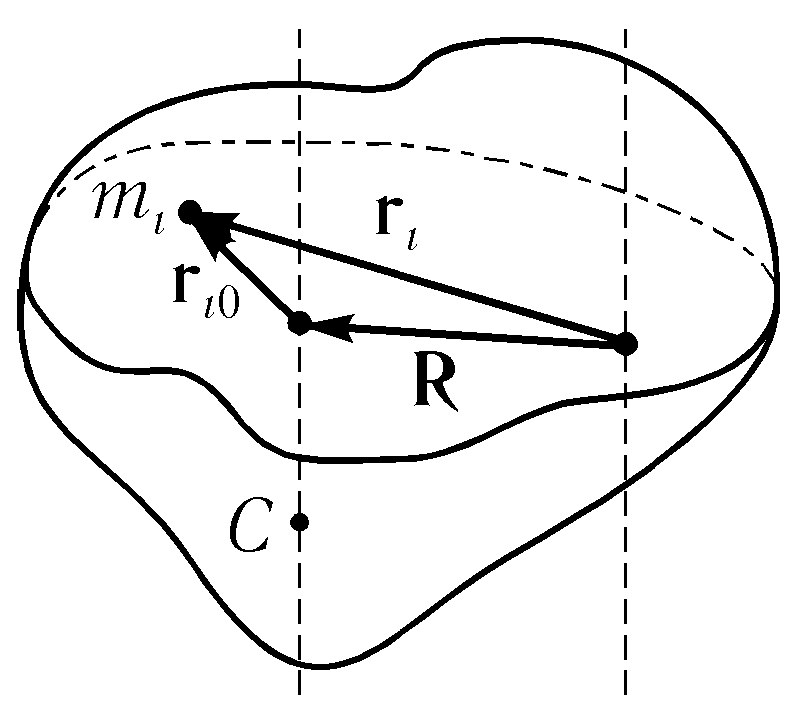
Рис. 7.9. К выводу теоремы Штейнера

Поэтому для определения М_осив конкретных задачах необходимо воспользваться тем, чтоМ_осиявляется, по определению, проекцией момента силыМотносительно

некоторого центра на ось вращения. Если ось вращения направлена вдоль

координатной оси Oz, то

М_оси = М_z = [rF]_z.

Покажем, как выражается M_0Cliчерез условия задачи о вращении тонкого диска

(рис. 7.10). Будем полагать, что центр О, относительно которого определен момент силы F, расположен в произвольной точке на оси вращения.

Разложим вектор силы F на три взаимно перпендикулярные составляющие, две из которых, F_||и F_h, параллельная и перпендикулярная оси вращения, лежат в плоскости, проходящей через ось вращения и точку приложения внешней силы, а третья F_┴— перпендикулярна к этой плоскости (эта составляющая обозначена на рисунке кружком с крестиком). Если в плоскости диска представить себе окружность радиуса h с центром на оси Oz, то составляющая F_┴будет направлена по касательной к этой окружности. Момент силы F относительно центра О равен сумме моментов составляющих:

М = М_|| + M_h + M_┴,

где

М_|| = [rF_||] , М_h = [rF_h], М_┴ = [rF_┴].

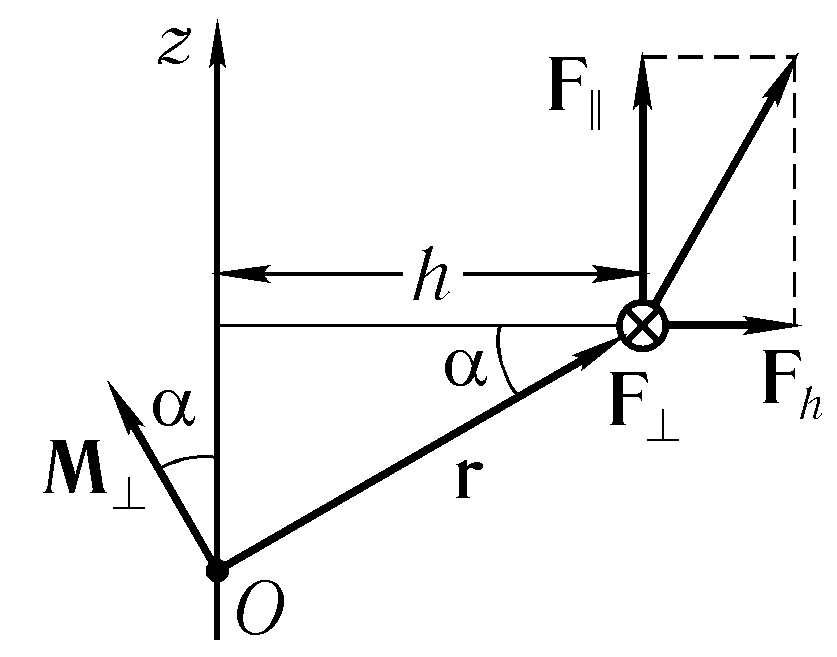Рис. 7.10

Векторное произведение направлено перпендикулярно плоскости, в которой лежат образующие его векторы. Поэтому векторы М_||и М_hперпендикулярны оси Oz, и следовательно, их проекции на эту ось равны нулю.

Момент М_┴ имеет модуль, равный rF_┴. Если составляющая F_┴на рис. 7.10

направлена «от нас», то ее момент М_┴по правилу винта направлен так, как

изображено на рисунке, т. е. образует с осью Oz угол а, косинус которого

равен h/r. Следовательно, в этом случае проекция на ось Oz вектора М_┴

положительна и имеет величину

М_┴cos(a) = hF_┴.

Если вектор F_┴направлен на рисунке «на нас», тоМ_┴ следут направить на рисунке в противоположную сторону, и тогда проекция этого вектора на ось будет иметь величину

М_┴ cos (π + а) = -hF_┴.

Другие компоненты М (М_||иM_hпроекций на ось

Oz, как уже отмечалось, не имеют. Следовательно,

M_z = M_┴,_Z = ±hF_┴.

Таким образом, получаем для момента силы относительно оси вращения:

М_оси =M_Z = ±hF_┴ . (7.21)

Подчеркнем еще раз, что по правилу винта знак «плюс» соответствует случаю, когда внешняя сила приводит к вращению вокруг направления оси Oz

против часовой стрелки, а знак «минус» соответствует вращению тела в

противоположном направлении.