Практическое занятие №4.

Практическое занятие «Определение параметров сечения Резерфорда на основе фитинга с данными NIST. (3-х часовое занятие). Определение первых моментов сечения, сравнение с даннымиNIST.

1. Цель работы:

1. расчет сечений упругого рассеяния электрона на ядре для случая кулоновского и обратно-квадратичного потенциала;

2. оценка параметров экранирования на основе сравнения расчетных сечений с литературными данными [1,2,3](NIST,MakKalumandBiggs,Salvat).

2. Теоретическое описание упругого рассеяния

1. Расчет сечения упругого рассеяния

Основной количественной характеристикой рассеяния является «сечение».

Рассмотрим мишень единичного объема, состоящую из достаточно большого числа n хаотично распределенных рассеивателей. На мишень падает поток частиц, с плотностьюj.

Рисунок 1

Эффективное поперечное сечение— в физике, величина, характеризующая вероятность перехода системы двух взаимодействующих частиц в определённое конечное состояние. Эффективное поперечное сечение определяется как отношение числа взаимодействийdNс заданными параметрами в единицу времени к плотности потока частиц, падающих на мишень.

Эффективное поперечное сечение имеет размерность площади.

Наглядно эту величину можно представить, как условное поперечное сечение частиц, из которых состоит мишень. При облучении этой мишени равномерным потоком, частицы, составляющие поток, должны попасть в это поперечное сечение. Частицы, которые «промахнутся» — не примут участия в рассматриваемом канале взаимодействия.

По аналогии с эффективным сечением вводится элементарное сечение – сечение рассеяния частица на одной частицы.

Дифференциальным сечением упругого рассеяния называется величина

2. Границы применимости

В основе анализа взаимодействия пучков частиц с твердыми телами лежат кинематические и динамические закономерности элементарного акта столкновения двух частиц. Классическая механика применима только тогда, когда можно пренебречь квантовыми эффектами. Это справедливо, если длина волны движущейся частицы становится меньше межатомного расстояния атомов твердого тела ∼0,1 нм [340]. Длина волны λ частицы массойM₁, имеющей скоростьvи кинетическую энергию E0 , определяется известным выражением

где h — постоянная Планка. Оценка λ < 0,1 нм дает приближенный предел применимости классической механики. Длина волны электронов приближается к этому пределу при энергиях меньше 150 эВ. Более точное исследование применимости классической механики принадлежит Бору. Его анализ показывает, что для малых углов рассеяния классический подход не оправдан, что также проявляется в неограниченном возрастании сечений по мере приближения угла рассеяния к нулю (большие прицельные параметры) для всех потенциалов с ограниченным радиусом действия. При квантовом подходе этого эффекта нет. Классический подход имеет не только нижний, но и верхний предел применимости по энергии. Это связано с тем, что расстояние между налетающей частицы и атомом мишени, например, при лобовом столкновении, может стать настолько малым, что становятся существенными квантово-механические эффекты.

3. Классический расчет

Для сравнительно больших энергий электрона, когда его длина волны много меньше размера атома, становится справедливой формула Резерфорда для дифференциального сечения упругого рассеяния. Получить точное выражение для формулы Резерфорда можно, исходя из приближенных вычислений. Рассмотрим электрон, налетающий со скоростью V₀на ядро с прицельным параметром равным. Масса ядра считается много большей массы электрона.

Рисунок 2

По определению

где dS– площадь кольца

Таким образом, дифференциал сечения можно рассчитать по формуле:

Из законов сохранения энергии и импульса с учетом следует, что модуль скорости электрона не изменится¹. Из рассмотрения рис. 3. получаем:

Рисунок 3

С другой стороны, изменение импульса тела равно импульсу силы

Заметим, что сила взаимодействия электрона с ядром сначала растет, затем, убывает. Исходя из этого, сделаем допущение, упрощающее расчет, но, тем не менее, приводящее к правильному результату: считаем, что взаимодействие электрона с ядром происходит только на расстоянии и на отрезке длиной. Тогда

Подставляя и в , получим:

С учетом того, что , приходим к выражению:

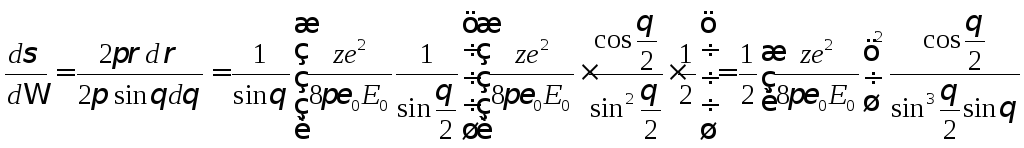
Домножая числитель и знаменатель на и применяя формулу двойного угла для синуса, получим:

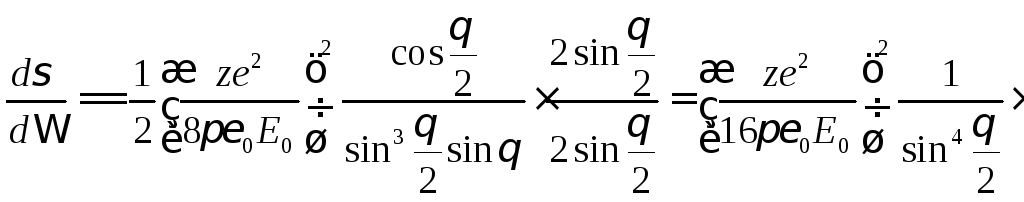
Таким образом, мы получили формулу Резерфорда для дифференциального сечения упругого рассеяния:

Полное сечение выражается следующим интегралом:

Проанализируем полученный результат. Несмотря на приближенность нашей модели, полученная формула позволяет отследить качественно важные зависимости.

1. Квадратичная зависимость от заряда ядра z.

2. Обратно квадратичная зависимость от энергии электрона E₀.

Приближенная модель привела к бесконечно большим значениям при нулевых углах рассеяния и расходимости интеграла . Для того, чтобы сечение сделать было конечной величиной, введем так называемый параметр экранирования .

Тогда формула модифицируется:

Параметр экранированияявляется достаточно малой величиной, и существенно сказывается лишь при углах рассеяния в окрестности.

Этой формулой можно пользоваться для расчета дифференциального сечения электронов больших энергий (без учета релятивизма).

4. Квантовый вывод в первом борновском приближении

Теперь получим формулу для сечения упругого рассеяния методами квантовой механики.

Рассмотрим частицу с импульсом , которая рассеивается на потенциале . Энергия электрона считается много большей, чем глубина потенциальной ямы. Описание рассеяния будем вести на основе стационарного уравнения Шредингера:

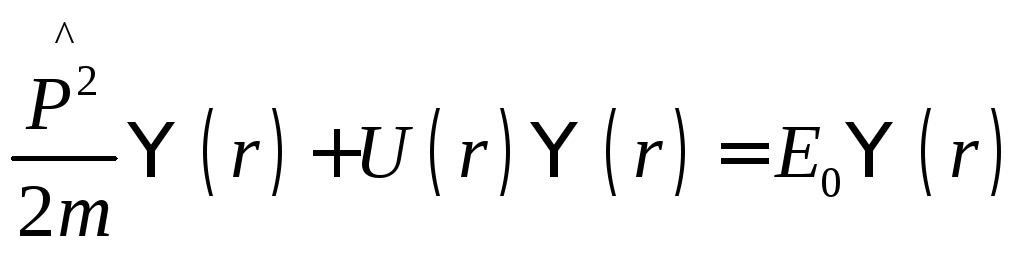
Основное уравнение теории рассеяния:

Пусть функция описывает состояние электрона до процесса рассеяния. Так как у электрона импульс известен точно, то, согласно принципу квантовой неопределенности, координата становится не определенной, а электрон представляется в виде волны:

Рассеянная волна представляется в виде расходящейся волны

где — амплитуда рассеяния.

Функция удовлетворяет уравнению без правой части:

Представим функцию в виде суммы:

Тогда с учетом и можно представить как:

Смысл первого Борновского приближения заключается в том, что мы пренебрегаем по сравнению с.

Решение уравнения

Рисунок 4

Для случая r >>R:. Следовательно.

Рассмотрим

Так как в волновой зоне, то

Сравнивая и , получаем

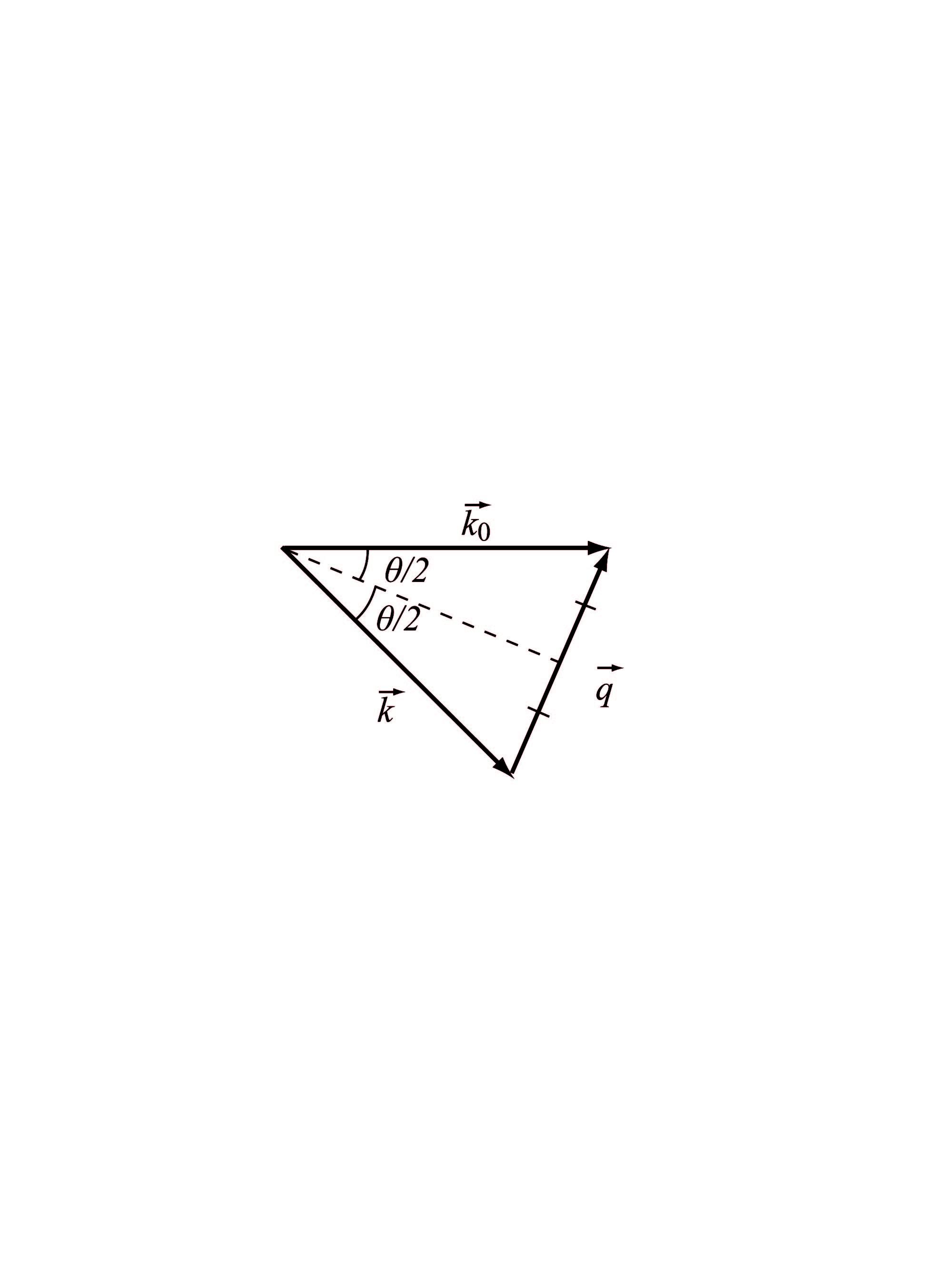
Рисунок 5

Из рассмотрения рис. 5:

Если подставить в кулоновский потенциал , то последний интеграл не существует.

Подставим кулоновский экранированный потенциал Юкавы , где- радиус атома-рассеивателя (в случае водорода это первый Боровский радиус)

Далее, представляя синус через экспоненты, имеем

Откуда получаем:

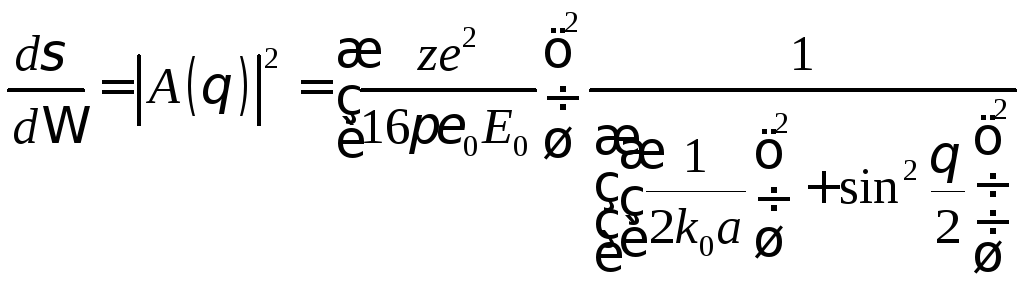
Обозначив за, получаем формулу , полученную ранее в классическом расчете.

Квантовая теория позволяет оценить величину , воспользовавшись тем, что:

Вспомним, что параметр был введен в классическом расчете для того, чтобы избавиться от бесконечно больших значений сечения при малых углах рассеяния. При, что соответствует большим энергиям рассеивающегося электрона и низкимZ рассеивающего ядра формула стремится к классической формуле Резерфорда .