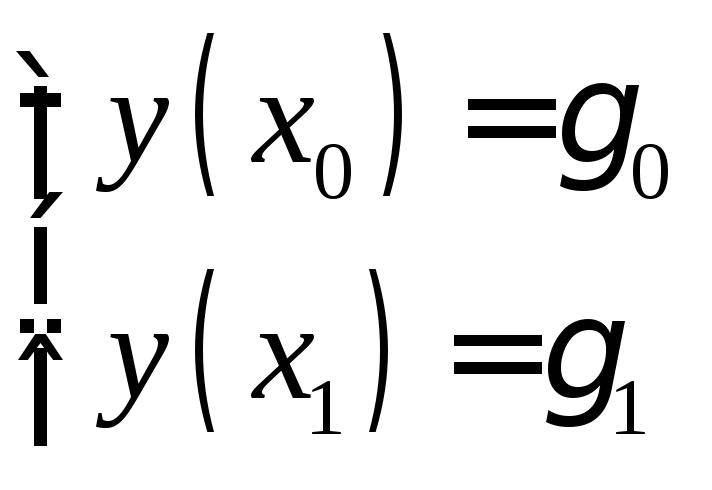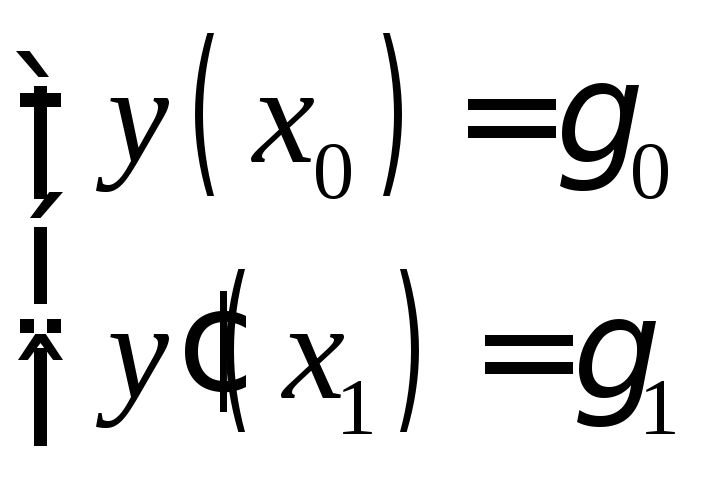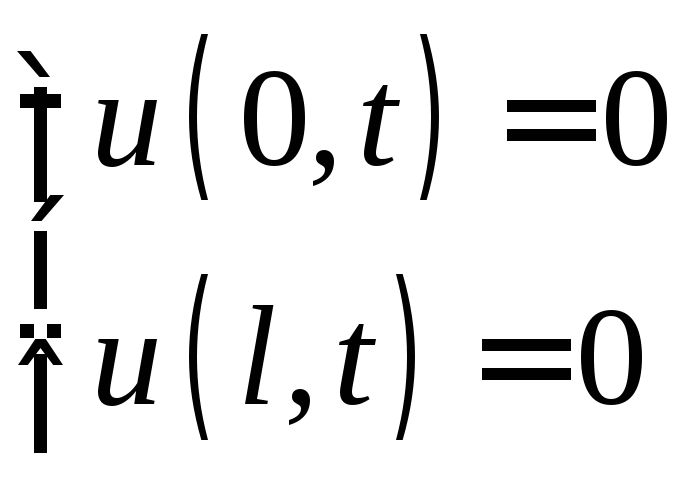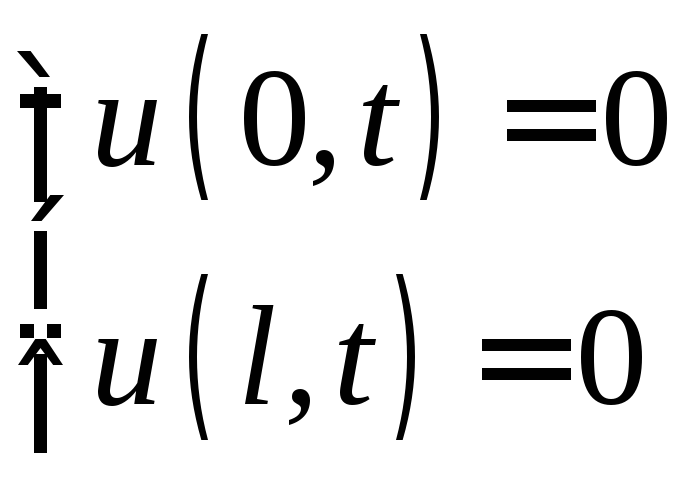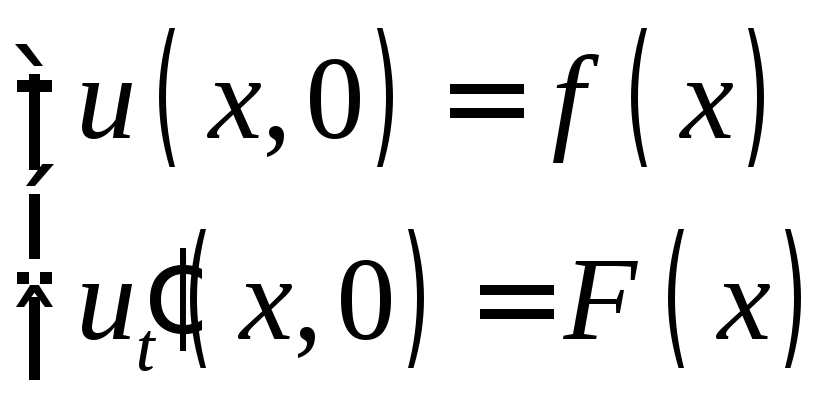Билет № 24

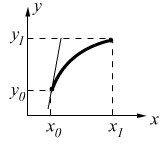
§ 10. Краевая задача для ЛДУ 2-го порядка.

1°.Постановказадачи.

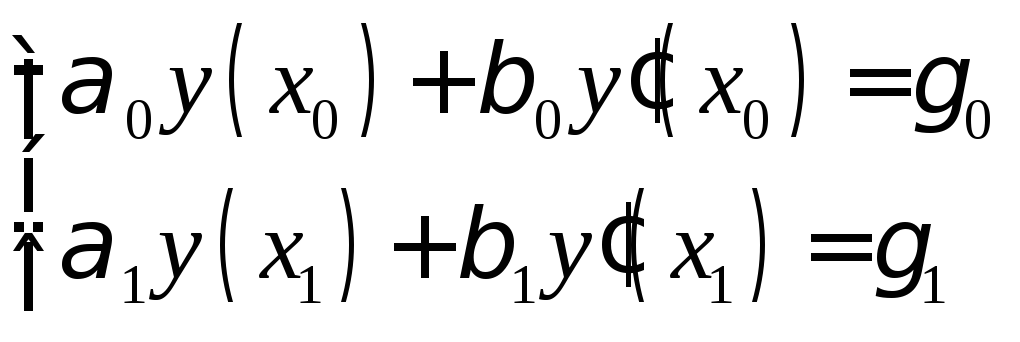
Опред.: Если , то краевые условия называются однородными.

Опред.: Если удовлетворяет краевым условиям, тоудовлетворяет однородным краевым условиям.

Пример 1:

Пример 2:

Билет № 25

2°. Задача Штурма-Лиувилля.

- непр.дифф.

, - непрерывны на,,на,.

Требуется найти все значения (собственное значение) при которых существует собственная функция, удовлетворяющая уравнению и краевым условиям.

Свойства собственного значения и собственной функции.

1. Существует монотонной возрастающая последовательность собственных значений , причемсоответствует собственная функция, обращающаяся в ноль ровнораз на.

2. Если , то все собственные значения положительны, за исключением случая,,,.

3. Собственные функции на отрезке образуют ортонормированную систему с весом, то есть(теорема Стеклова).

4. Всякая функция , удовлетворяющая краевым условиям и имеющая непрерывную 1-ю производную и кусочно-непрерывную 2-ю производную, разлагается в абсолютно и равномерно сходящийся ряд по собственным функциям:

, где .

Пример:

Характеристические корни: .

1). ,

.

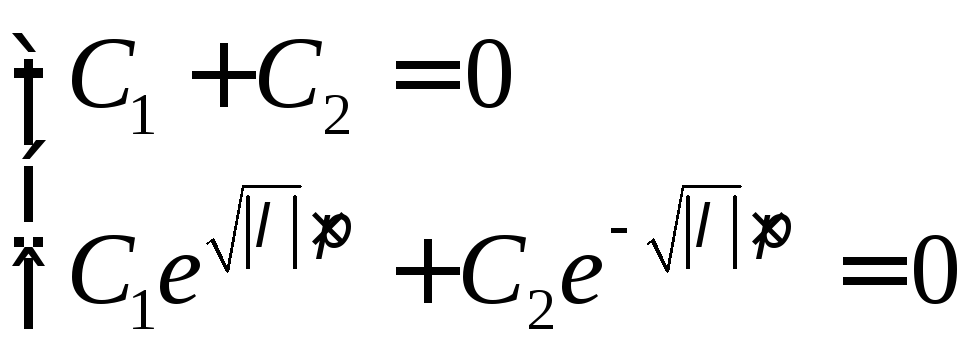
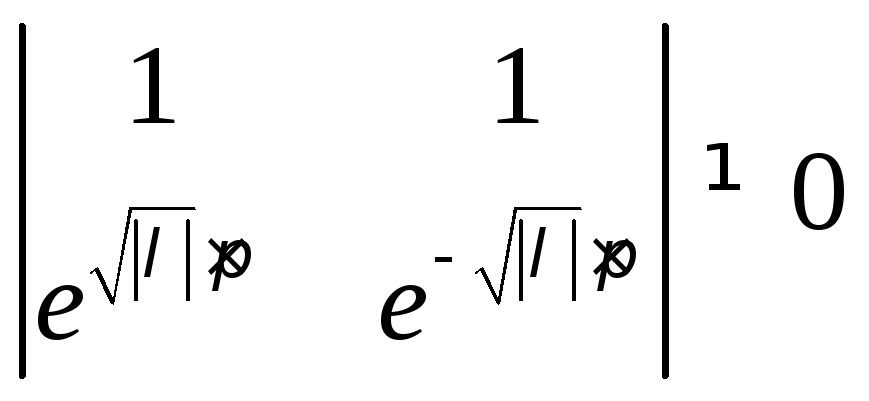
2). .

3).

; ,;

(, , )

,

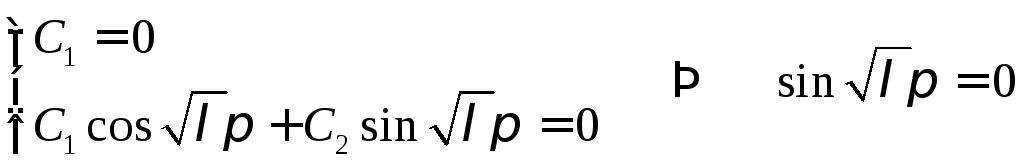- орт. на .

Билет № 26

§ 1. Классификация УРЧП.

1°. Определение.

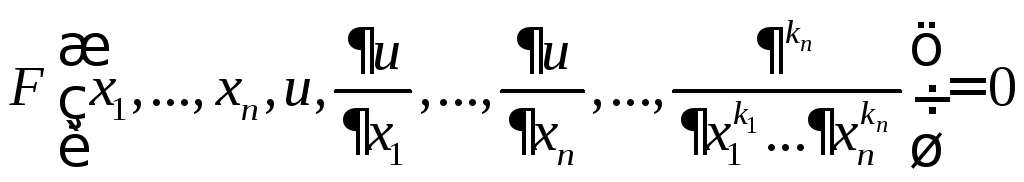Опред.: УРЧП – это у-е , где

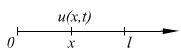- независимые переменные, .

Примеры у-ий в матфизике:

,

.

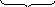
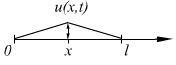2°. Линейные уравнения 2-го порядка от двух независимых переменных.

.

Существуют следующие типы таких уравнений:

Гиперболические:

Параболические:

Эллиптические:

3°. Уравнение характеристик.

,

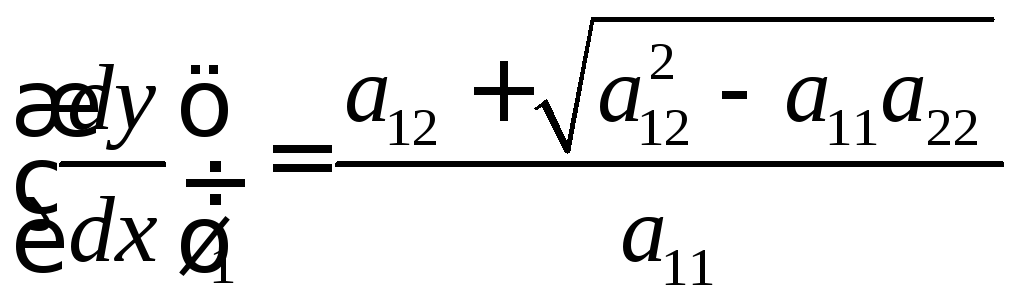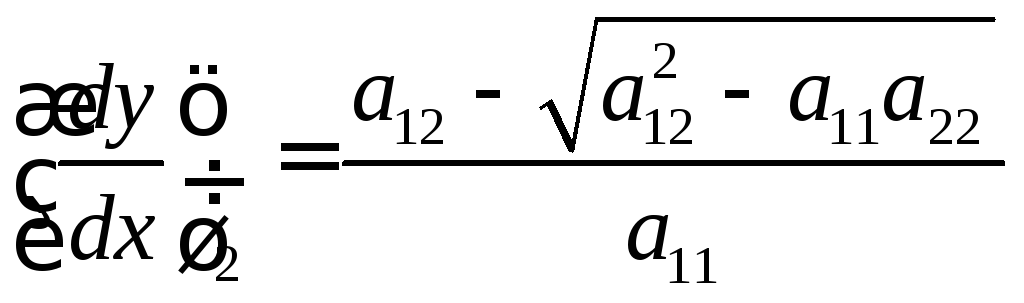
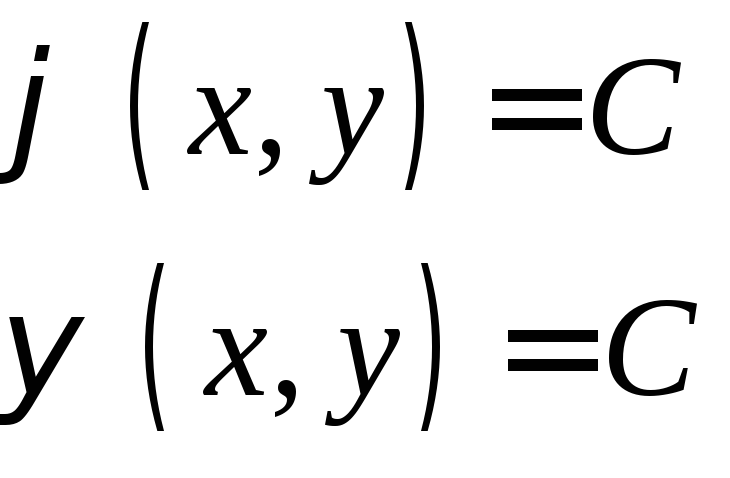- эти семейства кривых называются характеристическими кривыми (или характеристиками).

Если сделать замену переменных ,, и подставить ее в исходное уравнение, оно существенно упростится.

.

Билет № 27

4°. Приведение к каноническому виду линейных уравнений 2-го порядка от двух независимых переменных.

,

Гиперболический тип.

.

Можно считать, что (так как если, то в исходном уравнении меняются местами переменныеи. Если же, то вообще решать нечего).

Следовательно, ,.

.

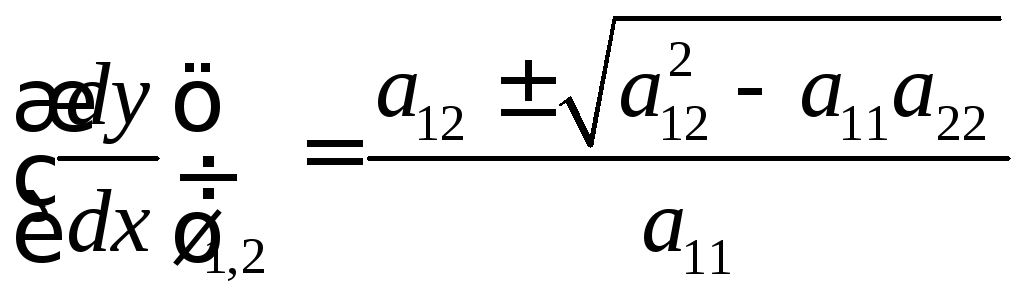
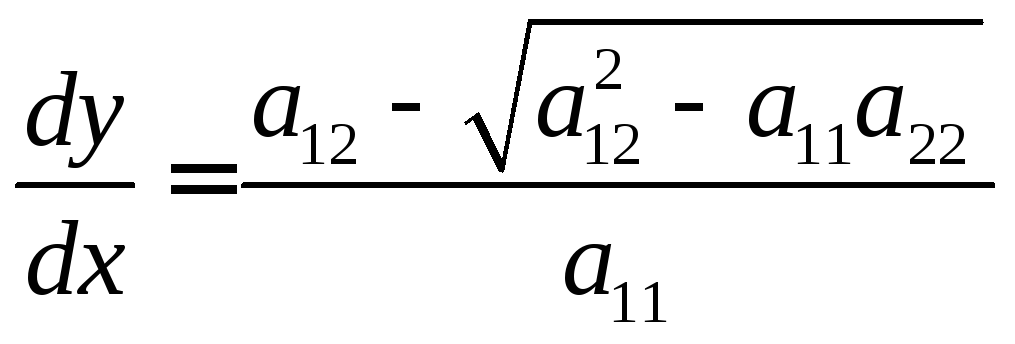
Билет № 28

4°. Приведение к каноническому виду линейных уравнений 2-го порядка от двух независимых переменных.

,

Параболический тип.

Можно считать, что ,.

,

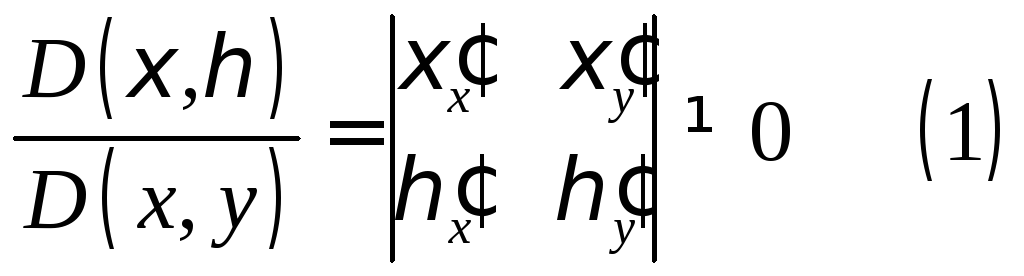
Эллиптический тип.

Можно считать, что (так как если, то, чего быть не может).

,

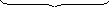
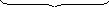Следовательно, .

.

Билет №29

§ 2. Колебания бесконечной струны.

1°. Постановка задачи.

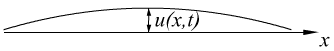
Опред.: Струна бесконечная - то есть колебания на одном конце струны очень нескоро дойдут до другого конца.

Н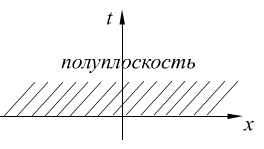ачальные условия:

Нужно найти положение струны в заданный момент времени в полуплоскости.

2°. Формула Даламбера.

3°. Физический смысл.

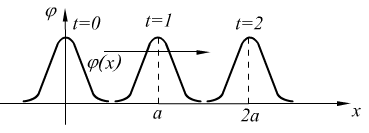
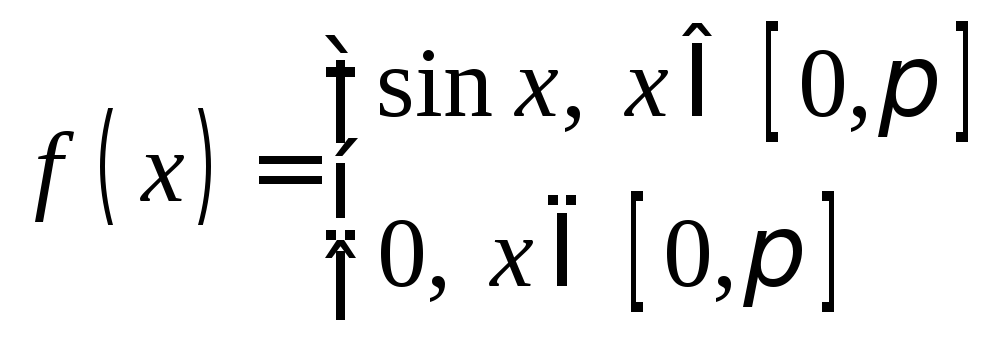
бегущая волна

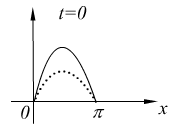
Билет № 30

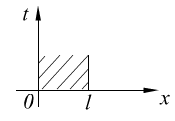
§ 3. Начально-краевая задача для уравнения 2-го порядка от двух независимых переменных.

1°. Постановка задачи.

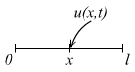
Краевые условия:

2°. Метод Фурье.

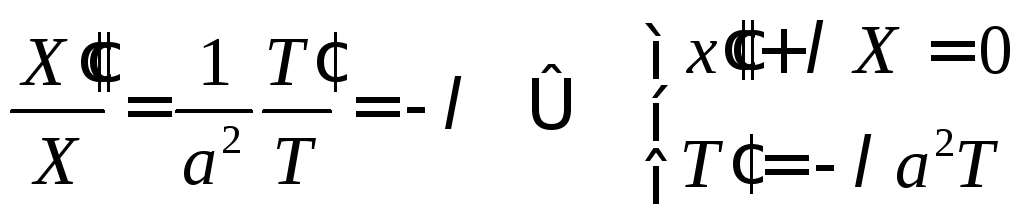
Если бы , то,,

, .

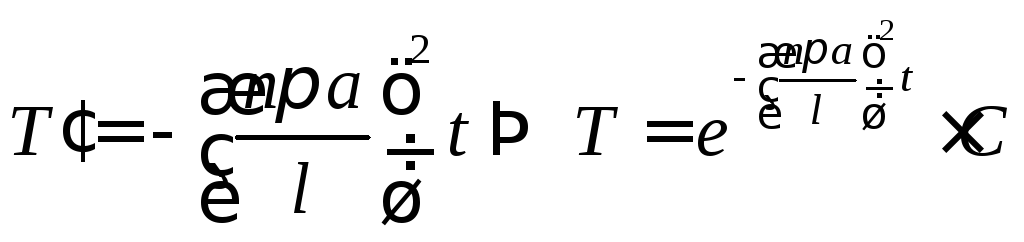
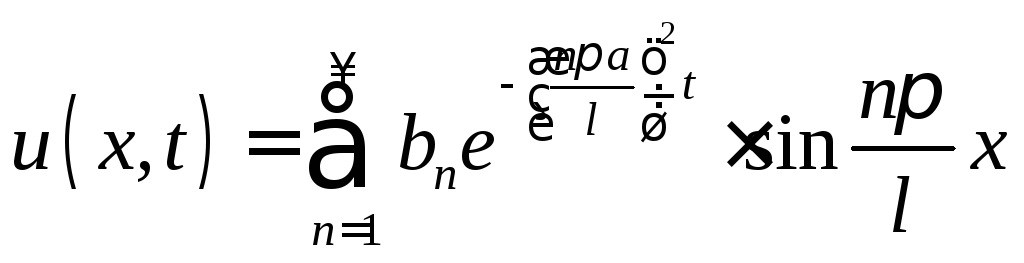
Если функция непрерывна и имеет кусочно-непрерывную производную, то тригонометрический ряд длясходится абсолютно и равномерно к.

Докажем, что производные исуществуют.

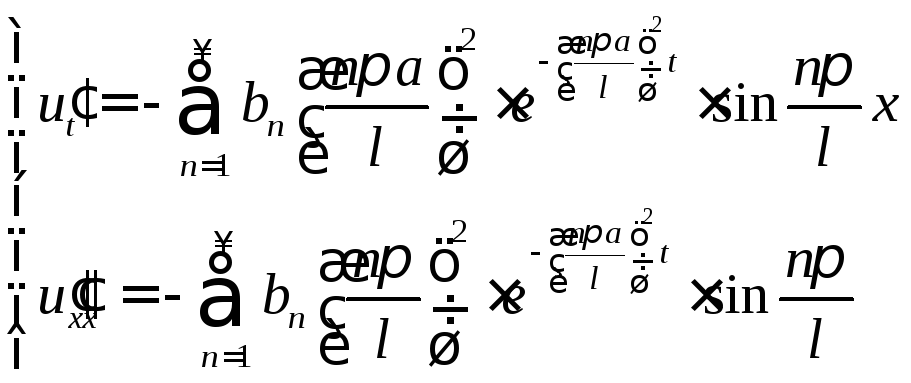- абсолютно и равномерно сходятся, так как:

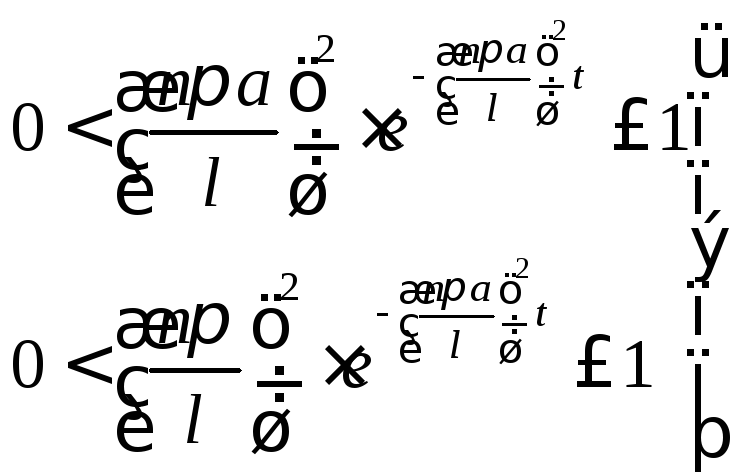
и достаточно больших .

Билет № 31

§ 4. Задача Дирихле для уравнения Лапласа.

1°. Постановка задачи для трехмерного тела.

2°. Задача Дирихле для круга.

,

,

, ,

,

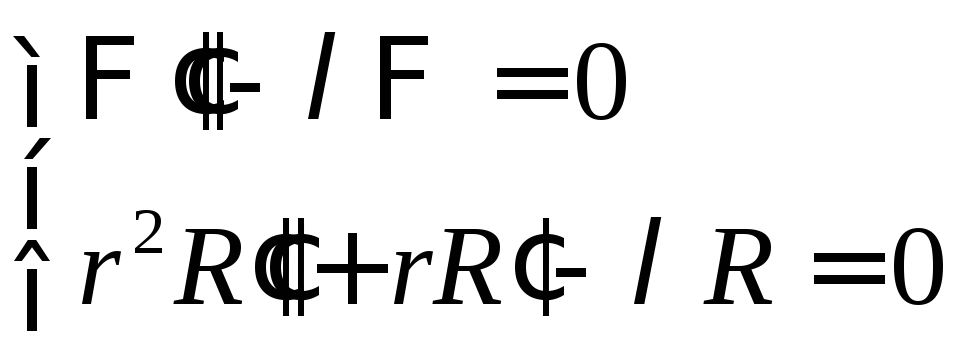
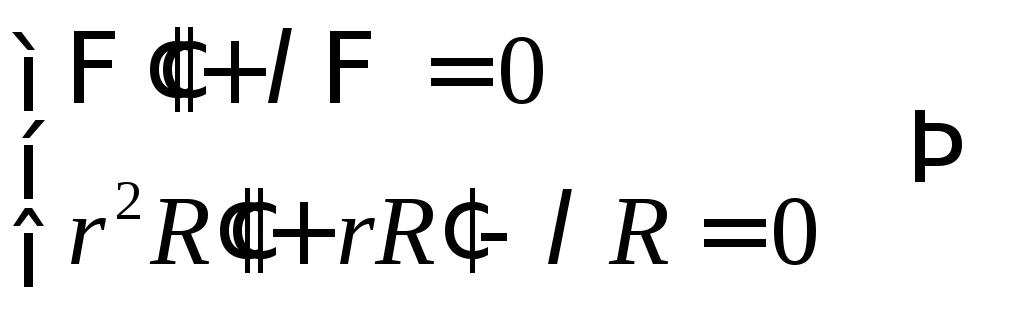
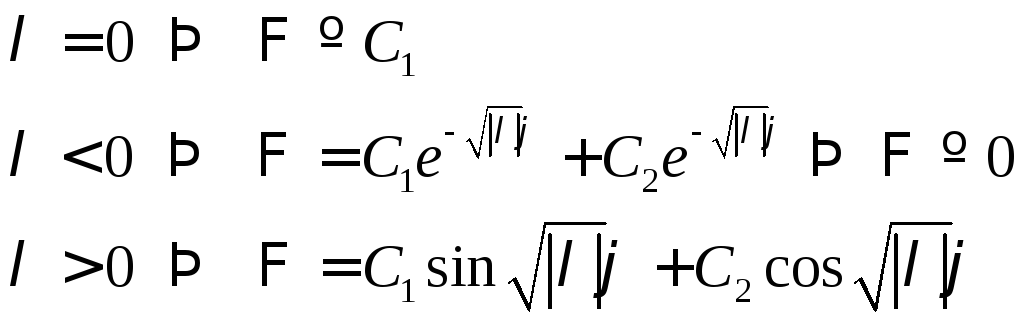
Подставляем во второе уравнение , получаем:

Получилось уравнение Эйлера.

,

,

Если ,,,,,,

проинтегрировав, получаем (в нуле не определен, поэтому по смыслу задачи мы должны взять).

Получим: ,,

Любая функция этого набора удовлетворяет уравнению Лапласа. Рассматривая сумму этих функций, то есть ряд:

,

Должно быть справедливо для всех .

, ,

Билет № 32

3°. Интегральная функция Пуассона.

(ядро Пуассона)

{представим как сумму геометрической прогрессии}

.

.

.

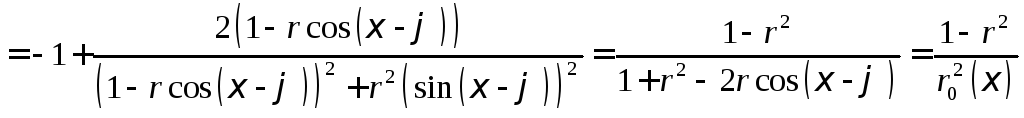4°. Формула Пуассона для шара.

.

Билет № 33

§ 5. Колебания закрепленной струны.

1°. Постановка задачи.

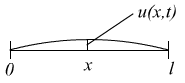
Уравнение колебаний струны:

Граничные условия:

Начальные условия:

2°. Метод Фурье.

Задача Лиувилля:

,

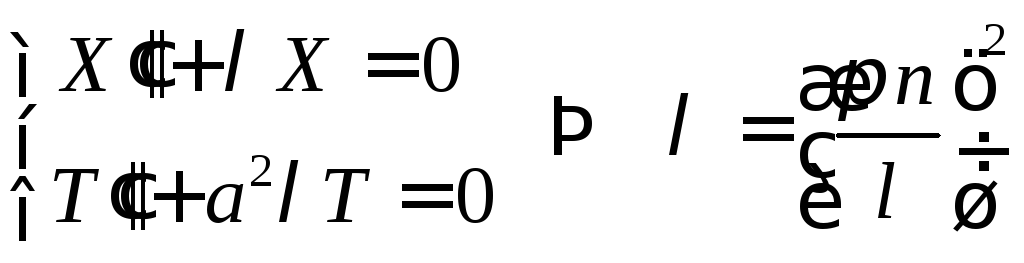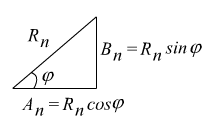
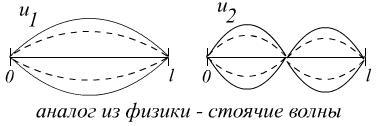
Билет № 34

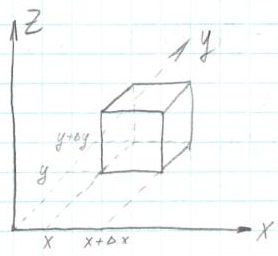
§ 6. Вывод уравнений математической физики.

1°. Уравнение теплопроводности.

Количество тепла, проходящее через левую грань куба справа налево за интервал времени (t,∆t+t), равно,α– коэффициент теплопроводности. , Общее количество тепла, входящее в Q, за интервал времени(t,t+∆t) , ,

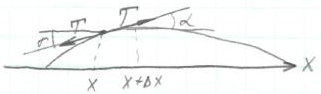
2°. Уравнения малых колебаний струны.

, = (x+∆x,t)

(x+∆x,t)-(x,t))=T(x,t)∆x

𝜌∆x(x,t)=T(x,t)∆x