§ 4. Уравнения 1-го порядка, неразрешенные относительно производной.

1°. Уравнение вида .

Дифференцируем по :

Решая это уравнение, находим либо. Тогдалибо.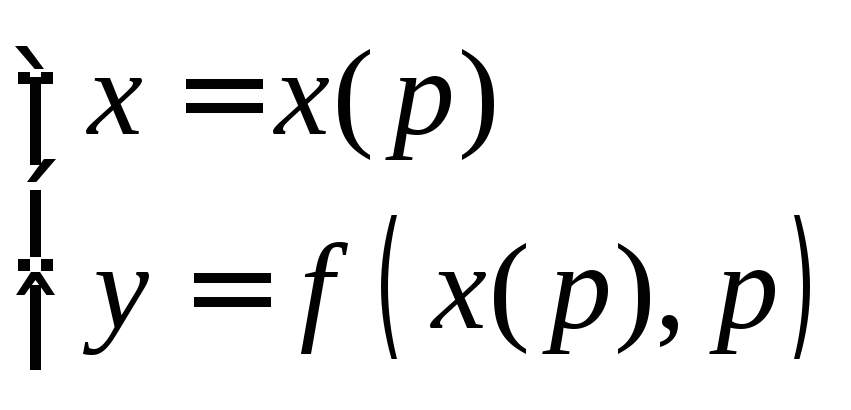

В этой системе можно: либо исключить , либо рассматривать её как параметрическое задание.

2°. Уравнение вида .

Дифференцируем по

Решая это уравнение, найдем либо.

Тогда, подставляя, получим:

либо

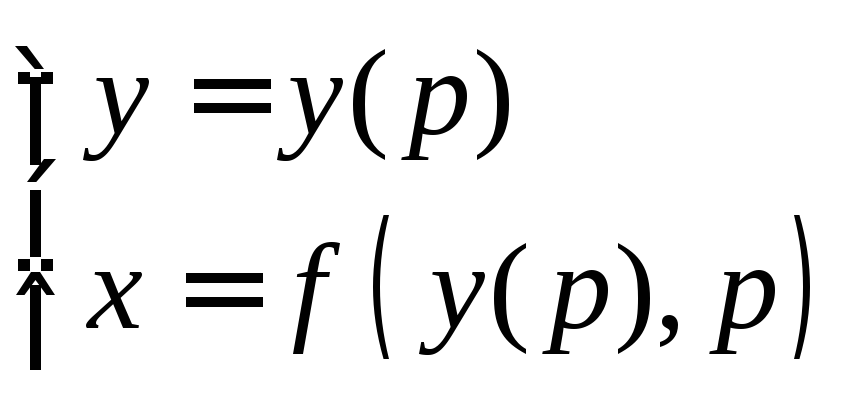
3°. Уравнение Клеро.

.

Билет № 7

§ 5. Дифференциальное уравнение, допускающее понижение порядка.

1°. Уравнения, не содержащие в явном виде.

2°. Уравнения, не содержащие в явном виде.

3°. Уравнения, однородные относительно .

.

Билет № 8

1°. Нормальная система.

Опред.: Нормальной системой называется совокупность уравнений вида:

, где - независимая переменная,

- искомые функции от ,- задание функции отпеременной.

Опред.: Нормальная система называется автономной (стационарной), если функции не зависят явно от, и неавтономной в противном случае.

Опред.: Решением нормальной системы на интервале называется совокупность функций, определенных на интервале, при подстановки которых все уравнения этой системы обращаются в тождествана интервале.

Опред.: Первым интегралом нормальной системы называется равенство , если оно выполняется для любого решения системы при соответствующем значении.

Опред.: Задачей Коши для нормальной системы называется задача нахождения решения этой системы, удовлетворяющего его условиям(начальное условие).

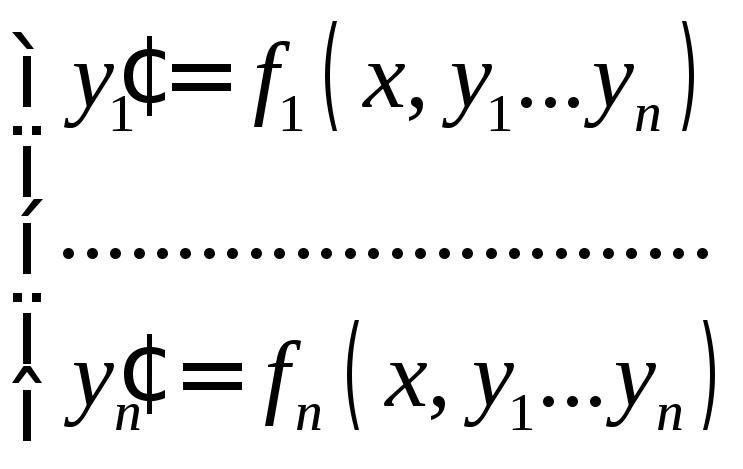
3°. Связь нормальных систем с общими дифференциальными уравнениями (оду) n-го порядка.

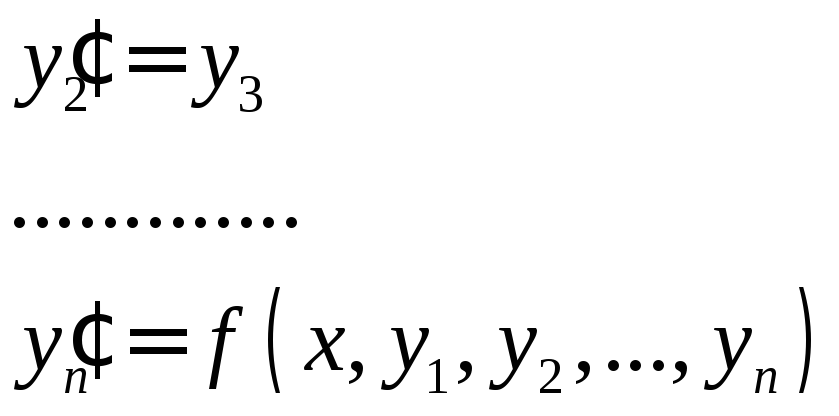
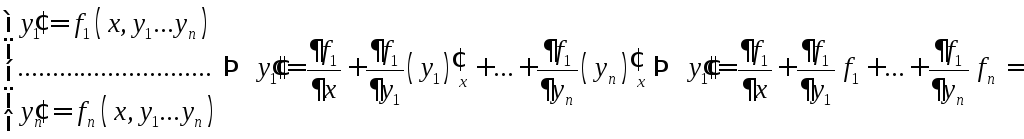
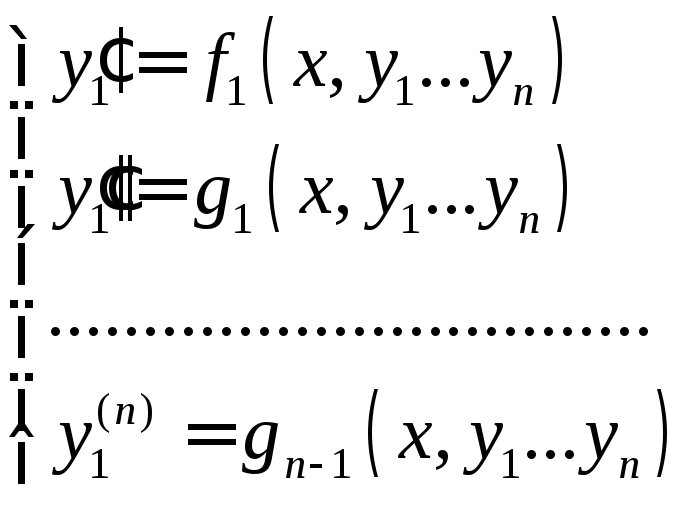
Исключим из этих уравнений переменные . Тогда у нас останется уравнение, которое получается методом подстановки.

Подставим в последнее уравнение вместо переменных их выражение через переменные

: .

Теорема (о существовании и единственности решения нормальной системы):

Пусть функции и их частные производные,непрерывны в некоторой области(расширенное фазовое пространство). Тогда для каждой точкисуществует отрезок, такой чтои единственное решение нормальной системы

, определенное на , удовлетворяющее условиям.

Доказательство:

(при интегрировании ).

.

Следствие (для дифференциальных уравнений - ного порядка):

Пусть правая часть дифференциального уравнения и её частные производныенепрерывны в некоторой области. Тогда для любой точкисуществует интервал, такой чтои единственное решение дифференциального уравнения, определенное наи удовлетворяющее условиям.

Опред.: Решение дифференциального уравнения - это функция от , это точка.

5°. Нормальная линейная система (нлс).

Теорема:

Пусть коэффициенты НЛС непрерывны на интервале, тогда для любых начальных значений, гдесуществует единственное решение НЛС, определенное на, удовлетворяющее начальным условиям

Билет №9

1°. Линейная однородная система (лос).

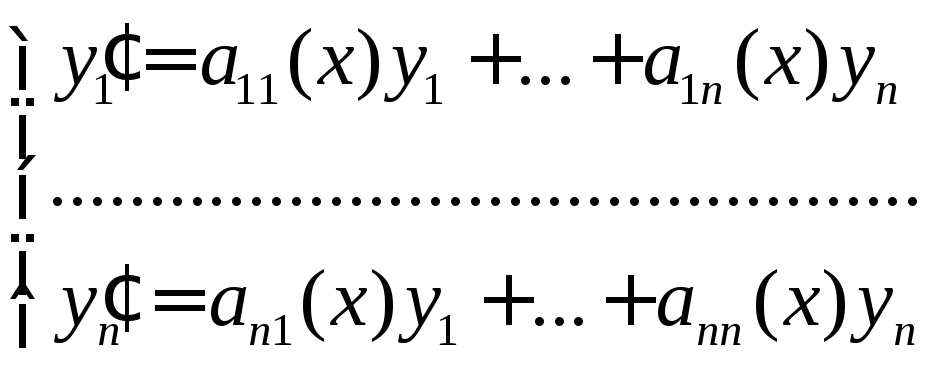
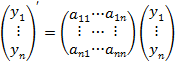
1. Если - решение ЛОС наи, тона.

2. Множество всех решений ЛОС является линейным пространством.

- решение ЛОС - решение

- решение - решение.

Коммутативность, ассоциативность, дистрибутивность следуют из аналогичных свойств операций с - мерными векторами.

3. Теорема: Решения линейно зависимы тогда и только тогда, когда они линейно-зависимы хотя бы при одном значении.

Доказательство:

.

.

Рассмотрим .

4. Размерность пространства решений ЛОС равна числу уравнений в системе.

Рассмотрим линейно-независимые постоянные вектора .

.

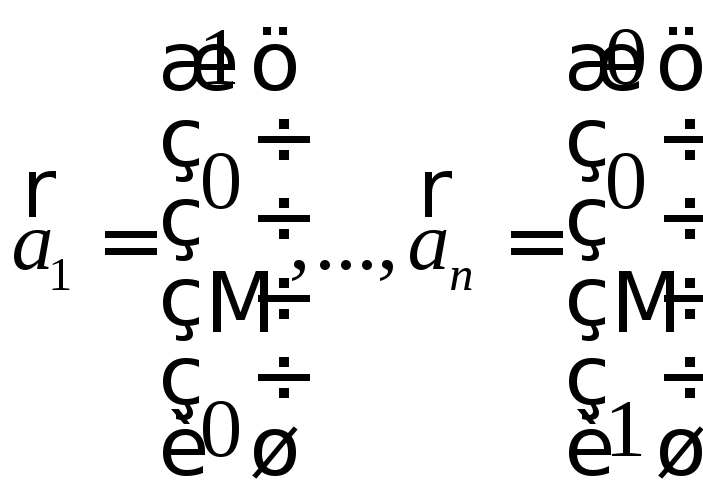По теореме о существовании и единственности существует решение ,

.

Эти решения линейно независимы согласно пункту 3.