1.2. Операции над множествами

Множества можно определять при помощи операций над некоторыми другими множествами и подмножествами. Пусть дана некоторая совокупность предметов, которую можно обозначить как множество

V ={ a, b, c, d, e, f, g, h, i, j, k }.

Предположим, что часть предметов, а именно: a, b, d и f имеют круглую форму, а часть – b, c, d, h, и i – окрашена в белый цвет. В этом случае говорят, что множество V имеет два подмножества А = { a, b, d, f } и В = { b, c, d, h, i } круглых и белых предметов. Можно говорить иначе: исходное множество называется фундаментальным или универсумом, а подмножества А и В – просто множествами.

В результате получим четыре класса элементов:

С₀ ={ e, g, j, k } – элементы, которые не обладают ни одним из названных свойств,

С₁ ={ a, f } – элементы, обладающие только свойством А (круглые),

С₂ ={ c, h, i } – элементы, обладающие только свойством В (белые),

С₃ ={ b, d } – элементы, обладающие одновременно двумя свойствами.

Операции над множествами удобно изображать с помощью графической диаграммы Эйлера-Венна (рис. 1).

Рис. 1 . Диаграмма Эйлера-Венна для двух множеств А и В

Объединением множеств А = { a, b, d, f } и В = { b, c, d, h, i } назовем множество А  В = { a, b, c, d, f, h, i }. Таким образом, объединением охватываются три класса элементов – С₁, С₂, С₃, которые на диаграмме заштрихованы (рис. 2). При этом оба множества могут и не пересекаться, т.е. не иметь общих элементов. Логическую операцию объединения двух множеств можно охарактеризовать словами: элемент принадлежит множеству А или множеству В. То, что элемент х принадлежит А или В, можно выразить формулой

х  А  В = (х  А)  (х  В),

где  – символ логической связки или, которая называется дизъюнкцией.

Пересечением множеств А и В называется множество K = А В, содержащее те элементы из А и В, которые входят одновременно в оба множества. Для нашего примера будем иметь (рис. 3):

K =А В = {a, b, d, f}  {b, c, d, h, i} = {b, d} = С₃.

То, что элемент х принадлежит одновременно двум множествам А и В, можно выразить формулой

х  А  В = (х  А) (х  В),

где  – символ логической связки и, которая называется конъюнкцией.

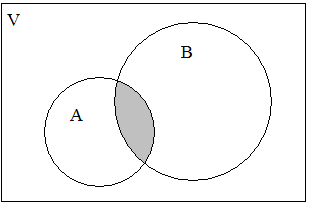
Рис. 2. А  В Рис. 3. А  В

Рассмотрим области С₁ и С₃, образующие множество А (рис. 4). Тогда области С₂ и С₀ образуют множество элементов, не входящих в А (рис. 5). Это обозначается как . Объединение или дизъюнкция множеств А и даст весь универсум V (А  =V), а пересечение или конъюнкция даст нам нулевое множество ; ( А = ). Таким образом множество дополняет множество А до универсума V, отсюда название – дополнительное множество или дополнение как операция. Операцию дополнения иначе еще называют инверсией.

Рис. 4. А Рис. 5.

После рассмотрения операции инверсии (дополнения) все четыре области С_j на диаграмме можно выразить следующим образом:

С₀ =  , С₁ = А  , С₂ =  В, С₃ = А  В.

Используя инверсию, можно представить любую множественную операцию, например объединение:

А  В = (А  ) ( В) (А  В).

Операции дополнения или инверсии объединения и пересечения множеств называются соответственно стрелкой Пирса (D =) и штрихом Шеффера (K =), которые обозначаются соответственно А↓В и А/В. Диаграммы для этих операций представлены на рис. 6 и 7.

Рис. 6. А↓В Рис. 7. А/В

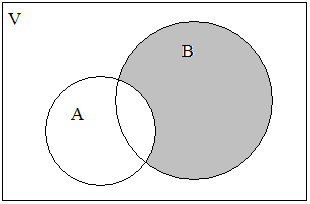
Рис. 8. ( В ← А ) Рис. 9. (В → А)

Разностью между множествами В и А называется совокупность тех элементов множества В, которые не вошли в множество А (рис. 8). Такая операция называется еще запретом А и обозначается ( В ← А ). Для нашего случая это будет область С₂.

При этом ( В ← А ) =  В.

Рис. 10. (А  В) Рис. 11. (А  В)

Дополнением к запрету служит импликация А. На диаграмме Эйлера-Венна это частичное включение множества В в множество А (рис. 9). Обозначается такая операция (В → А). При этом (В → А) = А  .

а b c

Рис. 12. (А  В)  (А  С)

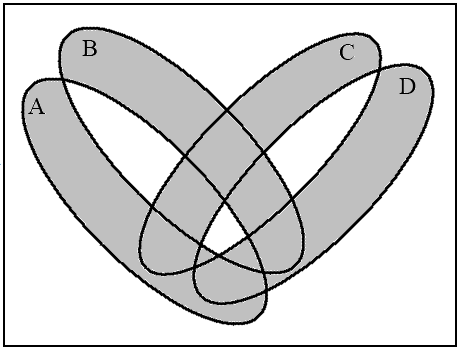
a (А  B) b ((А  B)→(C  D))

c ((А  B)/(C  D)) d ((А  B)→(C  D)) 

 ((А  B)/(C  D))

Рис.13. Диаграммы Венна для операций над четырьмя множествами

Аналогично определяются запрет В (А ← В) = А  и импликация В (А → В) =  В.

Остается привести еще две взаимно дополняющие операции – симметрическую разность или неравнозначность и эквивалентность или равнозначность.

Равнозначность определяется теми элементами множеств А и В, которые для них являются общими, а также элементами, не входящими ни в А, ни в В. В нашем случае это будут области С₀ и С₃ (рис. 10). Обозначается равнозначность А  В или А ~ В.

А ~ В = ( ) (А  В).

Неравнозначность есть объединение двух разностей или двух запретов. Эта операция обозначается (А  В). Таким образом,

(А  В) = (А ← В)  ( В ← А ), или (А  В) = ( В)  (А  ).

На диаграмме Эйлера-Венна это области С₁ и С₂ (рис. 11). Неравнозначность имеет еще название строгая дизъюнкция. Эту операцию можно передать словами: «либо А, либо В».

Диаграммы Эйлера-Венна достаточно наглядно иллюстрируют операции над тремя и четырьмя множествами. Рассмотрим операцию (А  В)  (А  С) и построим диаграммы Эйлера-Венна для трех множеств. Диаграмма на рис. 12а изображает операцию (А  В), а на рис. 12b – (А  С). Конъюнкцию этих соотношений иллюстрирует результирующая диаграмма на рис. 12с.

Для четырех множеств четыре круга Эйлера не дают полную диаграмму Венна, поскольку их пересечение дает только 14 областей, а необходимо 16. Поэтому круги необходимо деформировать в эллипсы. Покажем на примере построение диаграммы для выражения ((А  B)→(C  D))  ((А  B)/(C  D)).

На рис. 13 изображены четыре диаграммы, соответствующие указанной последовательности операций. Последняя диаграмма (рис. 13d) является результирующей.