
SAT 8
.pdf
314 |
|
|
|
|
|
PART III / EIGHT PRACTICE TESTS |
19. If 82−x = 512x+1, what does x equal? |
USE THIS SPACE AS SCRATCH PAPER |
|||||
(A) |
− |
1 |
|
|
||
|
|
|||||
|
4 |
|
|
|
||
(B) |
− |
1 |
|
|
|
|
|
|
|||||
|
2 |
|
|
|
||
(C) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||
|
|
|
|
|
||
(D) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
||
(E) |
|
5 |
|
|
|
|
4 |
|
|
|
|
||
|
|
|
|
|
||
20.The graph of x 2 − y 2 − 3x + 4y − 5 = 0 is which of the following?
(A)a circle
(B)an ellipse
(C)a parabola
(D)a hyperbola
(E)a semicircle
1
21. If f (x) = x + 3 and g(x) = 4 − x , then f /g(−1) =
2
(A) 5
9
(B)
5
5
(C)
2
(D)6
(E)10
22.Given the set of data 1, 2, 2, 3, 3, 3, 4, 4, 4, 4 which of the following is a true statement?
(A)mean < median < mode
(B)mean ≤ median ≤ mode
(C)mean ≤ mode ≤ median
(D)median < mode < mean
(E)median < mean < mode
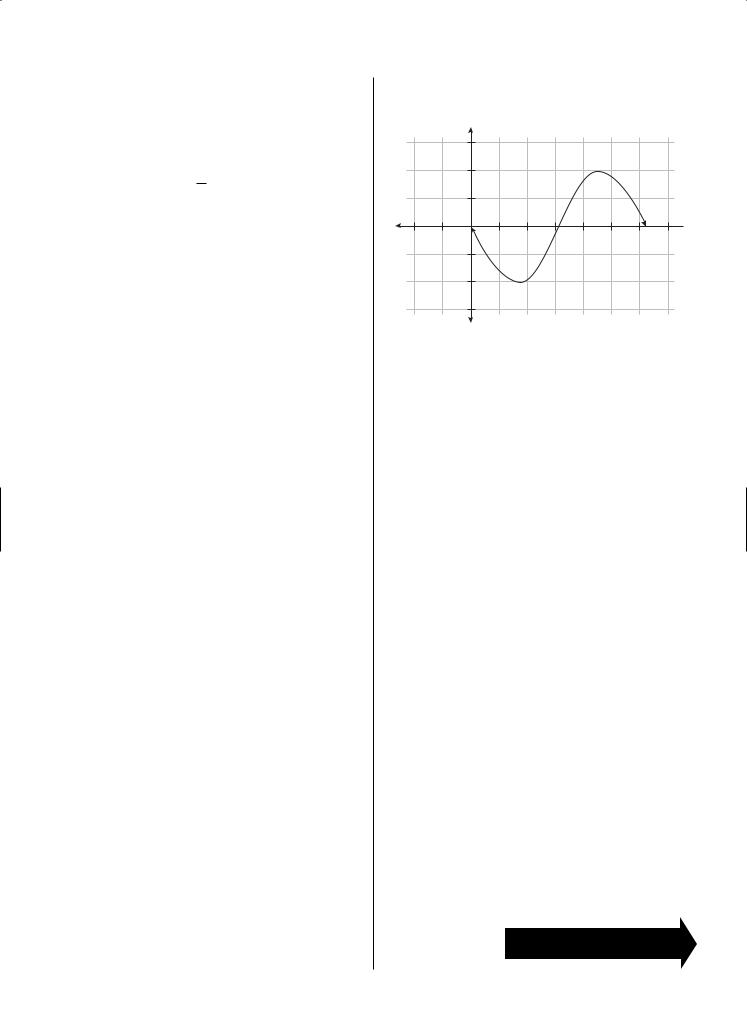
23.The graph of y = −2 cos πx has which of the following symmetries?
(A)Symmetric with respect to the y-axis
(B)Symmetric with respect to the x-axis
(C)Symmetric with respect to the origin
(D)Symmetric with respect to both axes
(E)None
GO ON TO THE NEXT PAGE

PRACTICE TEST 5 |
315 |
||
24. If 7, |
23 |
, and 16 are the first three terms of an arith- |
USE THIS SPACE AS SCRATCH PAPER |
|
|
||
2 |
|
|
|
metic sequence, then what is the sum of the first |
|
||
15 terms of the sequence? |
|
||
(A)77
(B)472.5
(C)577.5
(D)945
(E)1,155
25.A laptop purchased new for $2,800 depreciates at a rate of 22% per year. How much is it worth after 30 months?
(A)636
(B)1,505
(C)1,621
(D)1,874
(E)2,034
26.Which of the following is the solution of 2x − 4 < 1?
(A)3 < x < 5
2 2
(B) x < 5 2
(C)x < 3 or x > 5
2 2
(D)x > 0
(E)x ≤ 3 or x ≥ 5
2 2
27.Which of the following is the equation of a line with x-intercept (−3, 0) and y-intercept (0, −5)?
(A)5x + 3y = 15
(B)3x + 5y = −15
(C)5x − 3y = −15
(D)5x + 3y = −15
(E)−5x + 3y = 15
GO ON TO THE NEXT PAGE


318 |
PART III / EIGHT PRACTICE TESTS |
38. What is the length of the segment connecting |
USE THIS SPACE AS SCRATCH PAPER |
A(0, −1, 7) to B(5, 4, −2)? |
|
(A)7.7
(B)8.7
(C)10.7
(D)11.4
(E)131
39.Kate needs to complete 5 more courses: calculus, English, French, computer science, and history, in order to graduate from high school. She plans to schedule the courses during the first 5 periods of the school day, and all 5 courses are offered during each of the 5 periods. How many different schedules are possible?
(A)25
(B)24
(C)240
(D)120
(E)60
40.If the operation ♦ is defined for all real numbers a and b as a ♦ b = b2a. If n ♦ 5 = 125, then n =
(A)1
(B)2
(C)3
3
(D) 2
1
(E)
2
41.If the pattern of the terms 3 3, 27, 81 3, K continues, which of the following would be the 6th term of the sequence?
(A)(3 3)6
(B)( 3)6
(C)36
(D)(3 3)5
(E)37
42.What is the length of the minor axis of an ellipse whose equation is 25x2 + 9y2 − 18y − 216 = 0?
(A)3
(B)5
(C)6
(D)9
(E)10
GO ON TO THE NEXT PAGE

PRACTICE TEST 5 |
|
319 |
||
43. Which of the following is the equation of a circle |
USE THIS SPACE AS SCRATCH PAPER |
|||
with center (−1, 7) and a radius of length 3? |
|
|||
(A) |
(x + 1)2 − (y + 7)2 = 9 |
|
||
(B) |
(x + 1)2 + (y − 7)2 = 3 |
|
||
(C) |
(x − 1)2 |
+ (y + 7)2 = 3 |
|
|
(D) |
(x + 1)2 |
+ (y − 7)2 = 9 |
|
|
(E) |
(x − 1)2 |
+ (y + 7)2 = 9 |
|
|
44. lim |
8x2 − 11x + 3 |
= |
|
|
x2 − 1 |
|
|||
x →1 |
|
|
||
(A)1.7
(B)2.2
(C)2.5
(D)3
(E)No limit exists.
45.If a function is an even function, then f (−x) = f (x) for all values of x in the domain. Which of the following is an even function?
(A)f (x) = tan x
(B)f (x) = x + 1
(C)f (x) = x3 − 1
(D)f (x) = 2x
(E)f (x) = x 4 − 2x 2 + 7
46.If x = arctan(− 4) and x + y = 320°, then cos y =
(A)− 0.44
(B)0.24
(C)0.73
(D)0.81
(E)1
47. If i2 = −1, then which of the following equals
1
(5 − 12i)2 ?
(A)2 − 2i
(B)3 − 2i
(C)2 + 2i
(D)3 + 2i
(E)2 + 3i
48.tan4 θ + 2 tan θ + 1 =
(A)sec2 θ
(B)2 sec2 θ
(C)sec4 θ
(D)cos4 θ
(E)1
GO ON TO THE NEXT PAGE





 x
x